Décoder l'angle alterne interne sans mémoriser par cœur
Imaginez des rails de train, bien droits et parallèles. Maintenant, visualisez une route qui les coupe. Cette intersection crée un ensemble d'angles. Les angles alternes internes sont ceux situés entre les rails, de chaque côté de la route, mais en diagonale l'un par rapport à l'autre. Comme si vous regardiez à gauche puis à droite de la route, sans jamais quitter l'espace entre les rails.
Ces angles sont importants en mathématiques. Au Québec, leur place dans le programme scolaire a même été renforcée après la réforme de 2004. Avant, on les abordait environ 1,2 fois par an. Depuis, l'angle alterne interne est introduit dès la 5e année du primaire et révisé près de 5 fois au secondaire. Un vrai bond en avant ! Besoin d'un rappel sur les angles et leurs relations ? N'hésitez pas à consulter cette ressource bien utile. Cette augmentation de la fréquence d'apprentissage montre bien l'importance de maîtriser ce concept fondamental.
Alors, pourquoi certains élèves ont-ils du mal avec ces angles ? Souvent, le problème ne vient pas de la complexité du concept, mais de la façon dont on l'explique. Oublions les définitions trop abstraites ! L'essentiel est de bien visualiser la situation. L'image des rails et de la route peut vraiment aider. Besoin d'un coup de pouce supplémentaire ? Les services de tutorat de Centrétudes peuvent vous accompagner. Avec une approche visuelle et concrète, l'angle alterne interne devient beaucoup plus intuitif. Plus besoin de mémoriser des règles par cœur, on comprend vraiment comment ça marche.
La propriété des angles alternes internes : un jeu d'enfant !
Imaginez vos lignes de cahier. Parallèles, bien droites. Maintenant, tracez une ligne qui les traverse, comme si vous les coupiez avec votre stylo. Vous venez de créer le contexte parfait pour comprendre les angles alternes internes.
Ce sont des angles qui se trouvent de part et d'autre de la ligne que vous avez tracée (la sécante), mais "à l'intérieur" des deux lignes parallèles. Un peu comme si vous jouiez à cache-cache avec eux, ils se cachent chacun d'un côté de la sécante, entre les deux parallèles.
L'égalité magique : une clé pour la géométrie
La propriété fondamentale des angles alternes internes est simple : ils sont toujours égaux. Si l'un mesure 70 degrés, l'autre mesurera aussi 70 degrés. C'est une règle d'or, un peu magique, qui simplifie beaucoup de choses en géométrie.
Reprenons l'image des lignes de cahier. Imaginez-les comme des rails de train, et votre stylo comme une route qui les croise. Les angles formés entre les rails, de chaque côté de la route, mais en diagonale, sont nos angles alternes internes.
Débloquer les problèmes : un outil puissant
Connaître cette propriété, ce n'est pas juste mémoriser une formule. C'est comme avoir une clé magique qui ouvre des portes. Si vous connaissez la mesure d'un seul angle alterne interne, vous déduisez instantanément la mesure de l'autre. Un angle de 110 degrés ? Son alterne interne : 110 degrés aussi !
Et ce n'est pas tout ! Cette propriété permet aussi de prouver que deux droites sont parallèles. Si deux angles sont alternes internes et égaux, alors les droites qu'ils forment sont forcément parallèles. C'est un raisonnement inverse, mais tout aussi puissant.
Pour aller plus loin et consolider vos connaissances en mathématiques, n'hésitez pas à consulter les ressources de tutorat en maths proposées par Centrétudes.
Afin de mieux visualiser les relations entre les différents types d'angles formés par une sécante et deux droites parallèles, voici un tableau récapitulatif :
Propriétés des angles formés par une sécante et deux droites parallèles
| Type d'angle | Position | Propriété | Exemple d'utilisation |
|---|---|---|---|
| Angles alternes internes | De part et d'autre de la sécante, à l'intérieur des parallèles | Égaux | Calculer un angle inconnu si son alterne interne est connu |
| Angles correspondants | Du même côté de la sécante, l'un à l'intérieur et l'autre à l'extérieur des parallèles | Égaux | Déterminer la mesure d'un angle extérieur à partir d'un angle interne |
| Angles alternes externes | De part et d'autre de la sécante, à l'extérieur des parallèles | Égaux | Trouver la mesure d'un angle inaccessible directement |
| Angles co-intérieurs | Du même côté de la sécante, à l'intérieur des parallèles | Supplémentaires (leur somme est égale à 180°) | Vérifier si deux droites sont parallèles |
Ce tableau résume les propriétés des différents types d'angles, permettant ainsi de comprendre leurs relations et leurs applications pratiques. La propriété des angles alternes internes est donc un outil essentiel pour naviguer dans l'univers de la géométrie. Elle relie différents concepts et simplifie la résolution de nombreux problèmes.
Identifier les angles alternes internes en trois étapes simples
Imaginez essayer de repérer des angles spécifiques dans une figure géométrique complexe. Un peu comme chercher une aiguille dans une botte de foin, n'est-ce pas ? Pas de panique ! Identifier les angles alternes internes devient simple avec une méthode claire et quelques astuces visuelles. Le schéma ci-dessous illustre les trois étapes clés pour y arriver.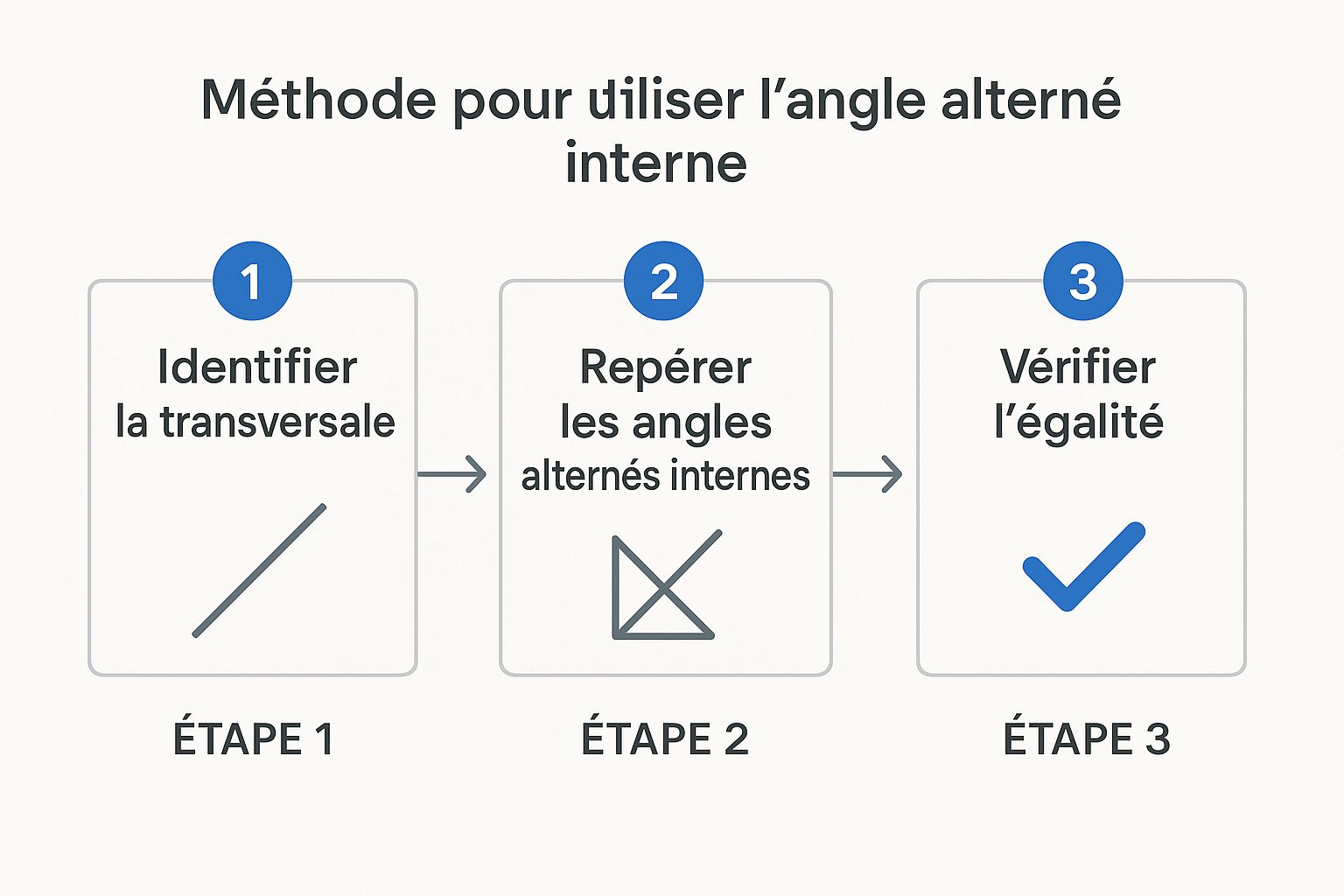 
Il vous guidera pas à pas, de la transversale jusqu’à la comparaison des angles.
Étape 1 : Identifier la transversale
Pensez à une route principale qui traverse plusieurs petites rues. Cette route principale, c'est notre transversale : la ligne droite qui coupe deux autres droites. Dans une figure géométrique, commencez par repérer cette ligne qui croise les autres. C'est le point de départ de notre exploration des angles.
Étape 2 : Repérer les angles alternes internes
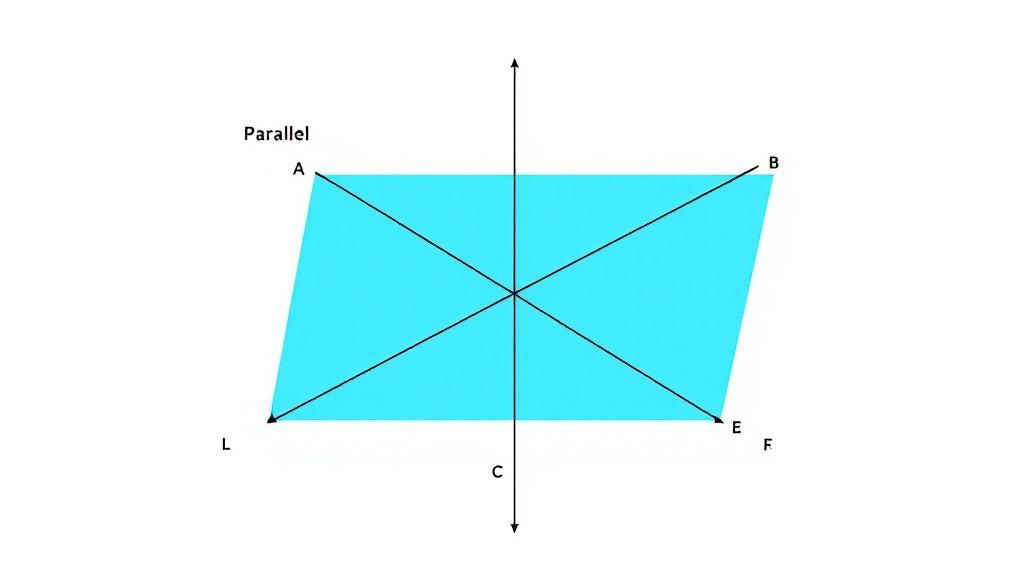
Une fois la transversale identifiée, imaginez deux enfants assis face à face de part et d'autre d'une table (notre transversale). Les angles que nous cherchons sont situés entre les deux droites coupées par la transversale, mais de chaque côté de celle-ci, comme les enfants à leur table. Ce sont les angles alternes internes. L'image ci-dessous, tirée de Netmath, illustre parfaitement ce positionnement. On voit bien la position des angles de chaque côté de la transversale et entre les deux autres droites.
Étape 3 : Vérifier l'égalité (si applicable)
Si les deux droites coupées par la transversale sont parallèles, comme des rails de train, alors les angles alternes internes sont égaux. C'est une règle d'or en géométrie. Si un angle mesure 50 degrés, son alterne interne mesurera aussi 50 degrés. Cette propriété est essentielle pour résoudre beaucoup de problèmes. Parfois, l'exercice ne précisera pas que les droites sont parallèles. À vous de le déduire, ou de le prouver, grâce à cette propriété des angles alternes internes !
Transformer la théorie en solutions concrètes
On a bien décortiqué la théorie des angles alternes internes, maintenant, place à la pratique ! Imaginez : vous construisez une cabane. Pour un toit solide, les poutres doivent être parallèles, et la poutre transversale doit former des angles précis. C'est là que nos angles entrent en jeu. Connaissant l'angle d'un côté de la poutre transversale, on peut trouver celui de l'autre côté grâce à leur égalité.
Si, par exemple, l'angle entre la poutre de gauche et la transversale est de 60 degrés, l'angle alterne interne, entre la poutre de droite et la transversale, sera aussi de 60 degrés. Voilà le secret d'une structure stable ! Et ce principe, on le retrouve partout : de la charpente aux ponts, en passant par les motifs géométriques. Au Québec, les profs insistent d'ailleurs sur l'importance de maîtriser ces angles : ils sont présents dans plus de 75 % des exercices de résolution de triangles au secondaire. Découvrez-en plus sur les angles et leurs relations.
Exemple concret : le jeu de billard
Prenons le billard. Imaginez les bandes comme des droites parallèles, et la trajectoire de la bille blanche comme une sécante. Quand la bille touche une bande, l'angle d'incidence (entre la trajectoire et la bande) est égal à l'angle de réflexion. Devinez quoi ? Ce sont des angles alternes internes ! En comprenant ce principe, on anticipe la trajectoire de la bille après le rebond et on vise juste. Même dans les jeux, la géométrie est cachée !
Des exercices pour consolider vos acquis
Prêts pour des exercices ? Dessinez deux droites parallèles coupées par une sécante. Nommez les angles. Identifiez les paires d'angles alternes internes. Si l'un mesure 120 degrés, combien mesure l'autre ? Repensez à la méthode en trois étapes : identifier la transversale, repérer les angles et vérifier l'égalité. Besoin d'un coup de pouce pour vos révisions ? Consultez nos conseils pour étudier efficacement.
Maîtriser les angles alternes internes, c'est plus que de la géométrie, c'est développer une vraie capacité d'analyse et de résolution de problèmes concrets. Un atout pour l'école et pour la vie !
Maîtriser par la pratique avec des exercices progressifs
Imaginez les angles alternes internes comme deux personnes assises face à face sur un banc, de part et d'autre d'un dossier. Le dossier, c'est la sécante, et le banc, ce sont les deux droites parallèles. Ces personnes se regardent : elles occupent des positions « alternées » par rapport au dossier et sont toutes deux « à l’intérieur » des parallèles. C'est l'idée de base des angles alternes internes.
Pour bien les maîtriser, rien de tel que la pratique ! Nous allons donc explorer des exercices, du plus simple au plus complexe.
Exercices de niveau débutant : Identifier et calculer
Commençons par un petit jeu d’observation. Tracez deux droites parallèles et coupez-les par une sécante. Repérez les paires d’angles qui ressemblent à notre exemple du banc. Ce sont vos angles alternes internes.
Maintenant, si l'un de ces angles mesure 45 degrés, combien mesure l’autre ? Et si l'un mesure 130 degrés, que peut-on dire de son alterne interne ? Ces exercices vous aideront à visualiser et à mémoriser la propriété fondamentale : les angles alternes internes sont égaux.
Exercices de niveau intermédiaire : Application de la propriété
Passons à la vitesse supérieure. Imaginez un triangle formé par nos deux droites parallèles et la sécante. Vous connaissez deux angles de ce triangle, dont un angle alterne interne. Comment trouver le troisième ? Ici, la propriété d'égalité des angles alternes internes devient un véritable outil de déduction. C'est comme une clé qui déverrouille la solution.
Il est intéressant de noter que, selon les résultats du ministère de l'Éducation du Québec pour l'année 2023, plus de 90 % des élèves reconnaissent la définition d'un angle alterne interne, mais seulement 65 % savent l’appliquer dans un problème complexe. Pour en savoir plus sur les angles alternes internes.
Exercices de niveau avancé : Problèmes à plusieurs étapes
Prêts pour un défi ? Imaginez une figure géométrique plus complexe, avec plusieurs droites parallèles et sécantes, comme un véritable réseau routier. Votre mission : calculer un angle précis. Vous aurez besoin de combiner la propriété des angles alternes internes avec d’autres notions géométriques, comme un détective rassemblant des indices.
Ces exercices vous aideront à développer votre flexibilité mentale et votre esprit de synthèse. Besoin d'un coup de pouce ? N'hésitez pas à explorer nos services de tutorat en mathématiques.
Avant de vous lancer, voici un tableau récapitulatif des types d'exercices que vous rencontrerez :
Types d'exercices sur les angles alternes internes par niveau de difficulté
Classification des exercices selon leur complexité et les compétences requises
| Niveau | Type d'exercice | Compétences testées | Temps moyen |
|---|---|---|---|
| Débutant | Identification et calcul direct | Reconnaissance et application de la définition | 5-10 minutes |
| Intermédiaire | Application de la propriété dans un triangle | Déduction et résolution d'équations simples | 10-15 minutes |
| Avancé | Problèmes à plusieurs étapes dans des figures complexes | Synthèse de plusieurs notions géométriques et raisonnement logique | 15-20 minutes |
Ce tableau vous donne un aperçu des défis qui vous attendent et du temps estimé pour chaque niveau. Chaque exercice est accompagné d'une solution détaillée et d'explications sur les erreurs fréquentes, pour vous aider à progresser efficacement.
Éviter les pièges classiques qui font trébucher
L'identification des angles alternes internes, ça peut parfois ressembler à un jeu de piste un peu complexe. On va démêler ensemble les erreurs les plus fréquentes pour que vous puissiez les éviter et progresser plus sereinement.
Confusion avec les angles correspondants
Imaginez encore nos rails de train et la route qui les croise. Un piège classique, c'est de confondre les angles alternes internes avec les angles correspondants. Ces derniers sont du même côté de la route : un entre les rails, l'autre à l'extérieur. L'erreur vient souvent d'une mauvaise identification de la zone "interne", celle qui se trouve précisément entre les deux lignes parallèles. Focalisez-vous bien sur cette zone entre les parallèles pour repérer les bons angles.
Négliger le parallélisme des droites
Un point crucial ! Nos angles alternes internes ne sont égaux que si les lignes droites coupées par la sécante sont bel et bien parallèles. Si ce n'est pas le cas, l'égalité ne tient plus. Avant toute chose, vérifiez donc ce parallélisme. C'est un détail qui peut sembler évident, mais qui est souvent la source d'erreurs.
Difficultés avec les figures complexes
Face à une figure complexe, avec un enchevêtrement de lignes et d'angles, il est facile de se sentir un peu perdu. La solution ? Décomposer la figure en éléments plus simples. Isolez chaque paire de droites parallèles et la sécante qui les coupe. N'hésitez pas à nommer chaque angle pour y voir plus clair. Une approche méthodique, c'est la clé pour naviguer dans ces figures complexes. Besoin d'un coup de pouce ? Centrétudes offre un service d'aide aux devoirs pour vous accompagner.
Manque de pratique
Comme pour tout en mathématiques, la pratique régulière est essentielle. Plus vous vous entraînerez à identifier et à utiliser les angles alternes internes, plus vous gagnerez en assurance. Créez vos propres exercices, variez les configurations, et consolidez vos acquis. C'est en forgeant qu'on devient forgeron !
En évitant ces pièges et en pratiquant régulièrement, vous maîtriserez rapidement les angles alternes internes. Vous pourrez les utiliser avec confiance dans vos problèmes de géométrie. Envie d'aller plus loin en maths et en français ? Jetez un œil aux services de tutorat offerts par Centrétudes.