Pour calculer l'aire d'un triangle, le secret, c'est une formule toute simple : on multiplie la longueur de sa base par sa hauteur, puis on divise le tout par deux. C'est la fameuse formule Aire = (base × hauteur) / 2. Elle fonctionne pour presque tous les triangles, qu'ils soient rectangles, isocèles ou scalènes. C'est le point de départ fiable et efficace que nous allons décortiquer ensemble.
Comprendre la formule de base et son application

Cette formule n'est pas sortie de nulle part. Elle est très visuelle. Imaginez simplement qu'un triangle est la moitié d'un rectangle. Si vous tracez une diagonale dans un rectangle, vous obtenez deux triangles parfaitement identiques. L'aire de chaque triangle est donc la moitié de celle du rectangle (longueur × largeur), ce qui nous amène directement à notre formule : (base × hauteur) / 2.
Identifier la base et la hauteur
Pour que le calcul fonctionne, il faut bien sûr savoir ce qu'on mesure. C'est là que la distinction entre la base et la hauteur devient cruciale.
- La base : C'est tout simplement l'un des trois côtés du triangle. On choisit souvent celui qui est à l'horizontale, celui sur lequel le triangle semble « posé », car c'est plus intuitif.
- La hauteur : Ici, il faut faire attention. La hauteur est la ligne qui part du sommet opposé à la base et qui descend pour former un angle droit (90°) avec cette base. Ce n'est pas toujours l'un des côtés du triangle!
Cette méthode est loin d'être nouvelle; elle est utilisée depuis des siècles, notamment pour des raisons bien pratiques comme l'arpentage des terres. Au Québec, sa maîtrise est un objectif clé du parcours scolaire. D'ailleurs, en 2020, plus de 90 % des élèves de 4e secondaire la maîtrisaient sans problème. Pour les curieux qui veulent creuser les origines de cette notion, cet article sur l'aire en géométrie) est une excellente ressource.
Un exemple concret pour démarrer
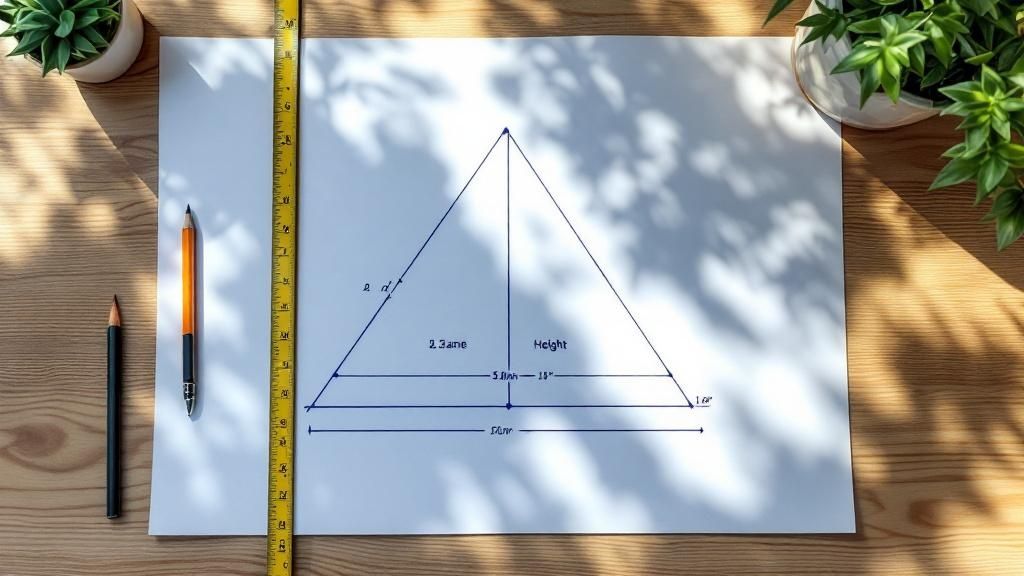
Mettons-nous en situation. Imaginez que vous devez coudre une petite voile de bateau en forme de triangle. Vous sortez votre ruban à mesurer. La base de la voile mesure 2 mètres. Ensuite, vous mesurez la hauteur, du milieu de la base jusqu'à la pointe, et vous trouvez 3 mètres.
Le calcul est un jeu d'enfant :
(2 m × 3 m) / 2 = 6 m² / 2 = 3 m².
Voilà! La surface de votre voile est de 3 mètres carrés. Avec cette approche simple, vous pouvez maintenant calculer l'aire de n'importe quel triangle avec confiance.
Adapter le calcul aux différents types de triangles
La formule universelle (base × hauteur / 2) est un excellent point de départ, mais la réalité, c'est que tous les triangles ne se présentent pas de la même façon. La nature même du triangle peut grandement simplifier la manière de trouver sa surface. Savoir adapter son calcul, c'est un peu comme avoir un tour de passe-passe mathématique dans sa poche.
Pour commencer, cette infographie résume bien le processus en trois étapes visuelles simples.
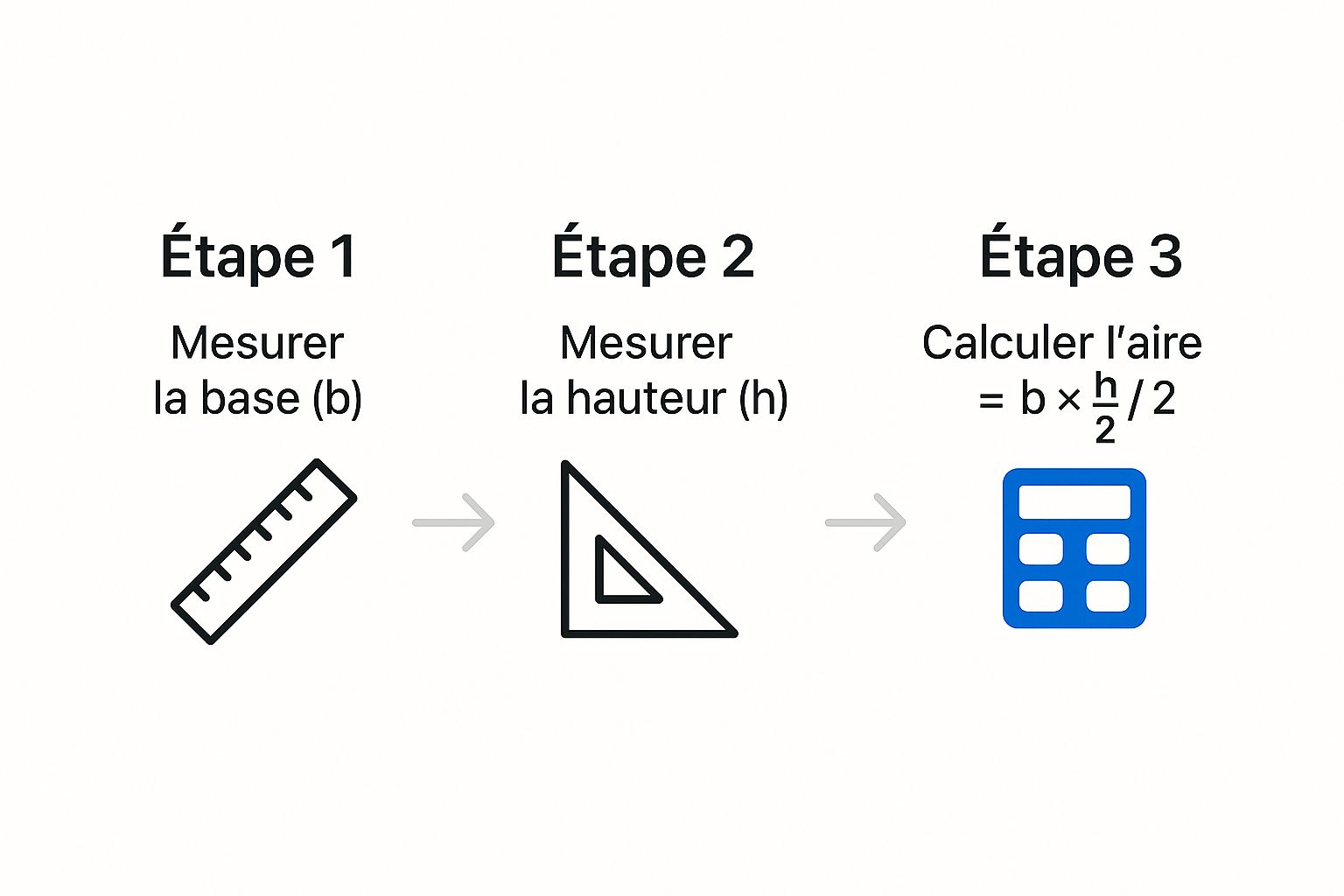
Ce visuel le montre clairement : peu importe la forme du triangle, le principe reste de mesurer la base et sa hauteur perpendiculaire. C'est l'identification de ces deux mesures qui change vraiment d'un type de triangle à l'autre.
Le cas du triangle rectangle
Le triangle rectangle, c'est le plus simple de tous. Oubliez la chasse à la hauteur! Les deux côtés qui forment l’angle droit de 90°, qu'on appelle les cathètes, jouent tout naturellement le rôle de base et de hauteur.
Il suffit donc de multiplier la longueur de ces deux côtés, puis de diviser le résultat par deux. C'est tout.
Exemple pratique : Vous voulez calculer la surface d'un pignon de toit qui est un triangle rectangle. Si une cathète mesure 4 mètres et l'autre 3 mètres, le calcul est direct : (4 m × 3 m) / 2 = 6 m². Pas besoin de sortir son ruban à mesurer pour autre chose!
Cette simplicité explique pourquoi on retrouve le triangle rectangle partout en architecture et en menuiserie, des domaines où les angles droits sont la norme.
Pour les triangles isocèles et équilatéraux
Avec un triangle isocèle (deux côtés égaux) ou équilatéral (trois côtés égaux), la hauteur n'est pas toujours une évidence. Heureusement, il y a une astuce.
La hauteur principale de ces triangles a la particularité de couper la base exactement en son milieu. En faisant ça, elle crée deux petits triangles rectangles identiques. C'est là que le fameux théorème de Pythagore (a² + b² = c²) entre en scène pour nous aider à trouver cette hauteur manquante.
- Pour un triangle isocèle : vous connaissez déjà la longueur du côté égal (qui devient l'hypoténuse de votre petit triangle rectangle) et la moitié de la base.
- Pour un triangle équilatéral : c'est encore plus simple, puisque tous les côtés sont de la même longueur.
Une fois que Pythagore vous a donné la hauteur, il ne reste plus qu'à revenir à la formule classique. Ça demande une petite étape de plus, c'est vrai, mais la méthode est infaillible. Maîtriser ces quelques calculs supplémentaires est essentiel. D'ailleurs, pour mieux comprendre comment consolider ces apprentissages, notre article sur l'importance des devoirs peut offrir des pistes intéressantes.
En comprenant ces quelques adaptations, vous voilà prêt à affronter n'importe quel triangle sans sourciller.
Calculer l'aire avec la formule de Héron (sans connaître la hauteur)

Mais que faire si on ne connaît pas la hauteur du triangle? C'est une situation bien plus courante qu'on ne le pense, surtout en arpentage ou en design, où mesurer une hauteur parfaitement perpendiculaire relève de l'impossible. Heureusement, il existe une solution : la formule de Héron.
Cette méthode est un véritable sauveur lorsque la formule classique (base × hauteur) / 2 n'est tout simplement pas applicable. Elle permet de calculer l'aire d'un triangle en se basant uniquement sur la longueur de ses trois côtés.
Décortiquer la formule de Héron
La formule peut sembler un peu intimidante à première vue, mais elle suit une logique très claire.
La voici : Aire = √[p(p-a)(p-b)(p-c)].
Chaque lettre joue un rôle bien précis :
- a, b, c : Ce sont tout simplement les longueurs des trois côtés de votre triangle.
- p : C'est le demi-périmètre du triangle. Pour le trouver, il suffit d'additionner les longueurs des trois côtés, puis de diviser ce total par deux. La formule est donc : p = (a + b + c) / 2.
Une fois le demi-périmètre (p) en main, le reste n'est qu'une question de remplacer les variables dans la formule de Héron et de faire le calcul. L'étape finale est d'extraire la racine carrée du résultat.
Bien qu'elle soit ancienne, la formule de Héron reste indispensable dans certains contextes. Une étude de 2023 a montré que seulement 15 % des étudiants québécois en maths avancées l'utilisaient régulièrement. Pourtant, sa précision est redoutable, surtout en topographie, où elle peut réduire la marge d'erreur à moins de 2 %. Pour creuser le sujet, la ressource d'Alloprof est un excellent point de départ.
Application sur un terrain complexe
Imaginons un cas concret : vous devez déterminer la superficie d'un lopin de terre triangulaire. Ses côtés mesurent 13 m, 14 m et 15 m. Dans cette situation, mesurer la hauteur perpendiculaire serait un vrai casse-tête.
-
D'abord, on calcule le demi-périmètre (p) :
p = (13 + 14 + 15) / 2 = 42 / 2 = 21 m. -
Ensuite, on applique la formule :
Aire = √[21(21-13)(21-14)(21-15)]
Aire = √[21 × 8 × 7 × 6]
Aire = √[7056] -
Et voilà le résultat final :
Aire = 84 m².
La surface de votre terrain est donc de 84 mètres carrés.
Maîtriser cette formule peut demander un peu de pratique, mais c'est une compétence incroyablement utile. Si ce genre de calculs vous donne du fil à retordre, un service de tutorat en maths peut vraiment vous aider à gagner en confiance et à devenir plus autonome.
Le calcul d'aire du triangle dans vos projets quotidiens
Savoir comment calculer l'aire d'un triangle est bien plus qu'un simple exercice de mathématiques. En réalité, cette compétence a des applications très concrètes qui peuvent vous faire économiser du temps et de l'argent dans une foule de projets à la maison. C'est le genre de notion qui sort des manuels scolaires pour s'inviter dans votre quotidien, que ce soit pour des rénos, du jardinage ou même des loisirs créatifs.
Pensez, par exemple, à la rénovation d'une chambre mansardée. Vous vous retrouvez face à ce fameux mur en pignon, cette grande surface triangulaire sous le toit, et vous devez le peindre. Un calcul juste de son aire vous permettra d'acheter la quantité exacte de peinture, et vous évitera le gaspillage d'un pot à moitié plein ou un aller-retour frustrant à la quincaillerie.
Optimiser vos projets et éviter le gaspillage
Cette logique s'applique à bien d'autres situations. Vous rêvez d'un petit potager dans un coin de votre cour? Si cet espace a une forme triangulaire, calculer sa superficie vous aidera à acheter la bonne quantité de semences et de terreau. Fini les surplus inutiles!
Même chose pour des projets de couture. Imaginez confectionner une jolie banderole de fanions ou une petite tente pour les enfants. Connaître l'aire des pièces de tissu triangulaires est essentiel pour acheter le métrage parfait. Un calcul précis, c'est la garantie d'économies et de projets réussis du premier coup.
Savoir calculer l'aire d'un triangle transforme une formule abstraite en un outil bien réel. Il ne s'agit plus de maths, mais de prendre des décisions éclairées, que ce soit pour un pot de peinture ou le plan d'un jardin.
Ce savoir-faire a aussi une valeur bien tangible sur le marché du travail au Québec. Selon des données de l'Institut de la Statistique du Québec, environ 12 % des emplois dans les secteurs de la construction et de l'architecture s'appuient sur ce type de calculs géométriques. Les professionnels du bâtiment, qui peuvent évaluer en moyenne 350 surfaces triangulaires par an, utilisent cette compétence pour optimiser l'aménagement de terrains et la conception de structures complexes, participant à des projets immobiliers d'envergure. Pour ceux qui veulent creuser le sujet, vous pouvez en apprendre davantage sur l'impact de ces calculs grâce à cette analyse détaillée.
Des applications pratiques et variées
Au-delà des économies, maîtriser ce calcul renforce la confiance et l'autonomie. Voici quelques exemples concrets où cette compétence devient un véritable atout :
- Aménagement paysager : Calculer la surface d'une pelouse triangulaire pour commander la bonne quantité de gazon en rouleaux.
- Décoration intérieure : Estimer la surface d'un mur d'accent triangulaire pour acheter le nombre juste de rouleaux de papier peint.
- Bricolage : Déterminer la superficie d'une étagère d'angle avant de la vernir ou de la recouvrir.
En intégrant ce calcul à vos réflexes, vous développez une meilleure vision dans l'espace et une approche plus méthodique de vos projets. Si la mise en pratique de ces notions vous semble encore un peu floue, un service d'aide aux devoirs et de soutien scolaire peut être une excellente ressource pour bâtir des bases solides et appliquer les mathématiques avec assurance.
Pièges courants et astuces pour des calculs précis
Même avec la bonne formule en poche, un calcul d'aire peut vite tourner au vinaigre à cause de quelques erreurs bien connues. Heureusement, en connaissant ces pièges, on peut facilement les éviter avec un peu de vigilance et de méthode.
La confusion la plus fréquente, et de loin, est de prendre un des côtés inclinés du triangle pour sa hauteur. C'est une erreur classique qui fausse complètement le résultat final.
Le truc à retenir est simple : la hauteur doit toujours former un angle droit (un angle de 90°) avec la base. En cas de doute, une petite ligne pointillée pour la visualiser mentalement ou sur papier fait toute la différence. C'est une habitude qui garantit d'utiliser la bonne mesure à chaque fois.
Attention aux détails qui changent tout
Un autre oubli courant est de sauter l'étape finale : la division par deux. Après avoir multiplié la base par la hauteur, on peut être tenté de s'arrêter là, mais on se retrouve alors avec le double de l'aire réelle.
Finalement, il y a la question des unités de mesure. Si vous mélangez des mètres pour la base et des centimètres pour la hauteur, par exemple, votre résultat sera mathématiquement incorrect.
Pour assurer des calculs sans faille, voici quelques réflexes à adopter :
- Vérifiez toujours la perpendicularité : Assurez-vous que votre hauteur est bien à 90° de la base choisie.
- Uniformisez vos unités : Avant de commencer le moindre calcul, convertissez toutes vos mesures (m, cm, mm) dans la même unité.
- Relisez la formule : Prenez une seconde pour vous rappeler qu'il faut diviser le produit de la base et la hauteur par deux.
Ces petites vérifications transforment le calcul de l'aire d'un triangle en un exercice simple et sans stress. Pour mieux organiser votre étude et retenir ce genre d'information, jetez un œil à nos conseils sur comment étudier efficacement.
Foire aux questions sur le calcul de l'aire d'un triangle
Même après avoir exploré les différentes formules, il arrive souvent que quelques questions persistent. Cette section est là pour répondre aux interrogations les plus communes et dissiper les derniers doutes sur les subtilités du calcul de l'aire d'un triangle.
L'objectif est de solidifier vos connaissances pour que vous puissiez aborder n'importe quel problème de géométrie avec une confiance totale.
Peut-on calculer l’aire avec seulement les angles?
C'est une excellente question, et la réponse est non. Connaître uniquement les trois angles d'un triangle ne suffit pas pour déterminer son aire. Pourquoi? Parce que les angles définissent la forme du triangle, mais pas sa taille.
Imaginez deux triangles qui ont exactement les mêmes angles : l'un pourrait tenir dans votre main, tandis que l'autre pourrait avoir la taille d'une maison. Pour calculer l'aire d'un triangle, il vous faut impérativement au moins une mesure de longueur, comme la base et la hauteur, ou encore les longueurs des trois côtés pour utiliser la formule de Héron.
Quelle est la différence entre l'aire et le périmètre?
Il est très facile de confondre ces deux notions, mais elles mesurent des choses complètement différentes. Pensez-y de cette façon :
- Le périmètre, c'est la longueur totale du contour du triangle. C'est la distance que vous parcourriez si vous marchiez le long de ses trois côtés. On l'obtient en additionnant les longueurs des côtés (a + b + c) et il s'exprime en unités de longueur (cm, m, etc.).
- L'aire, quant à elle, mesure l'espace à l'intérieur de ces côtés. C'est la surface que vous devriez peinturer, par exemple. Elle s'exprime en unités de surface (cm², m²).
Ne jamais confondre ces deux mesures est fondamental, que ce soit pour un projet de rénovation ou un simple devoir de mathématiques. Une bonne compréhension de ces concepts de base est souvent évaluée. Pour les élèves qui souhaitent se préparer au mieux, jeter un œil aux attentes d'un examen du ministère au secondaire peut être très éclairant pour cibler les notions clés.
Doit-on toujours utiliser la même unité de mesure?
Absolument. C'est une règle d'or et, croyez-moi, l'une des erreurs les plus fréquentes. Si la base de votre triangle est mesurée en mètres et sa hauteur en centimètres, vous devez impérativement convertir l'une des deux mesures avant de faire le moindre calcul.
Mélanger les unités, c'est la garantie d'un résultat erroné. Assurez-vous que toutes vos longueurs sont exprimées dans la même unité (par exemple, tout en centimètres) pour obtenir une aire juste. Votre résultat sera alors exprimé dans l'unité carrée correspondante (cm²).