Calculer le volume d’un cylindre peut sembler intimidant, mais c'est en réalité bien plus simple qu'on ne le pense. Tout repose sur une seule formule clé : V = π × r² × h. Une fois que vous avez le rayon (r) de la base et la hauteur (h) du cylindre, le plus dur est fait.
Les éléments essentiels pour calculer le volume d'un cylindre
Que vous ayez besoin de remplir une piscine, de mesurer la capacité d'un réservoir d'eau chaude ou simplement de résoudre un exercice pour l'école, la méthode ne change jamais. C'est une compétence pratique qui refait surface bien plus souvent qu'on ne l'imagine, bien au-delà des salles de classe. L'objectif est simple : déterminer l'espace total qu'occupe un objet en trois dimensions.

La formule V = πr²h est votre point de départ. Pour être certain de bien l'appliquer, il faut d'abord décortiquer chacun de ses composants.
Les variables à maîtriser
Chaque lettre dans cette formule représente une mesure précise de votre cylindre. Il est crucial de ne pas les mélanger.
Voici un petit tableau pour y voir plus clair.
| Les composants de la formule du volume | ||
|---|---|---|
| Symbole | Variable | Ce que ça représente |
| V | Volume | Le résultat final, c'est-à-dire la capacité du cylindre. Il s'exprime en unités cubiques (cm³, m³, etc.). |
| π | Pi | La fameuse constante mathématique. On utilise souvent l'approximation 3,14159, mais votre calculatrice a une touche dédiée pour plus de précision. |
| r | Rayon | La distance qui part du centre de la base circulaire jusqu'à son bord. C'est exactement la moitié du diamètre. |
| h | Hauteur | La distance qui sépare les deux bases circulaires du cylindre. |
En résumé, il suffit d'identifier ces éléments sur votre objet pour que le calcul devienne un jeu d'enfant.
L'erreur la plus fréquente? Confondre le rayon et le diamètre. Le diamètre, c'est la ligne qui traverse tout le cercle en passant par le centre. Le rayon n'en est que la moitié. Prenez toujours le réflexe de diviser le diamètre par deux avant même de commencer vos calculs!
Si ces concepts vous semblent encore un peu flous ou si vous voulez simplement solidifier vos bases, un accompagnement personnalisé peut tout changer. Le tutorat en mathématiques est un excellent moyen de gagner en confiance pour ensuite aborder des problèmes plus complexes sans hésiter.
En maîtrisant ces quatre petits éléments, vous vous assurez d'obtenir un résultat juste à tous les coups, que ce soit pour un projet de bricolage à la maison ou pour un devoir important.
Mesurer le rayon et la hauteur sans se tromper
Pour calculer le volume d’un cylindre, tout part de mesures justes. Les deux informations cruciales dont vous aurez besoin sont le rayon (r) et la hauteur (h). Croyez-moi, une petite erreur sur l’une de ces deux valeurs, et votre résultat final sera complètement à côté de la plaque.
Imaginez que vous voulez savoir combien de soupe contient une conserve. La hauteur, c’est assez simple : on la mesure avec une règle. Par contre, pour le rayon, ça se complique. Trouver le centre exact d’un cercle à l'œil nu, ce n’est pas évident.
Du diamètre au rayon : une étape clé
Dans la vie de tous les jours, il est bien plus simple de mesurer le diamètre. C'est la distance qui traverse le cercle d'un bord à l'autre en passant par le centre. Une fois que vous avez cette mesure, trouver le rayon devient un vrai jeu d'enfant.
Le rayon correspond toujours à la moitié exacte du diamètre. Si votre conserve mesure 8 cm de diamètre, son rayon est de 4 cm. C'est ce chiffre, et non 8, qu'il faudra utiliser dans la formule.
Un autre point essentiel est la cohérence des unités de mesure. Si votre hauteur est en centimètres, le rayon doit l'être aussi. Mélanger les mètres et les centimètres est une erreur classique qui fausse tout le calcul. Choisissez une unité et tenez-vous-y du début à la fin !
- Mesurer la hauteur (h) : Avec un ruban à mesurer ou une règle, mesurez simplement la distance entre les deux bases circulaires du cylindre.
- Mesurer le diamètre : Posez votre règle sur la base circulaire pour trouver la plus grande distance possible d'un bord à l'autre.
- Calculer le rayon (r) : Il suffit de diviser la mesure du diamètre par deux.
Cette petite illustration résume bien le processus pour vous aider à visualiser les étapes.
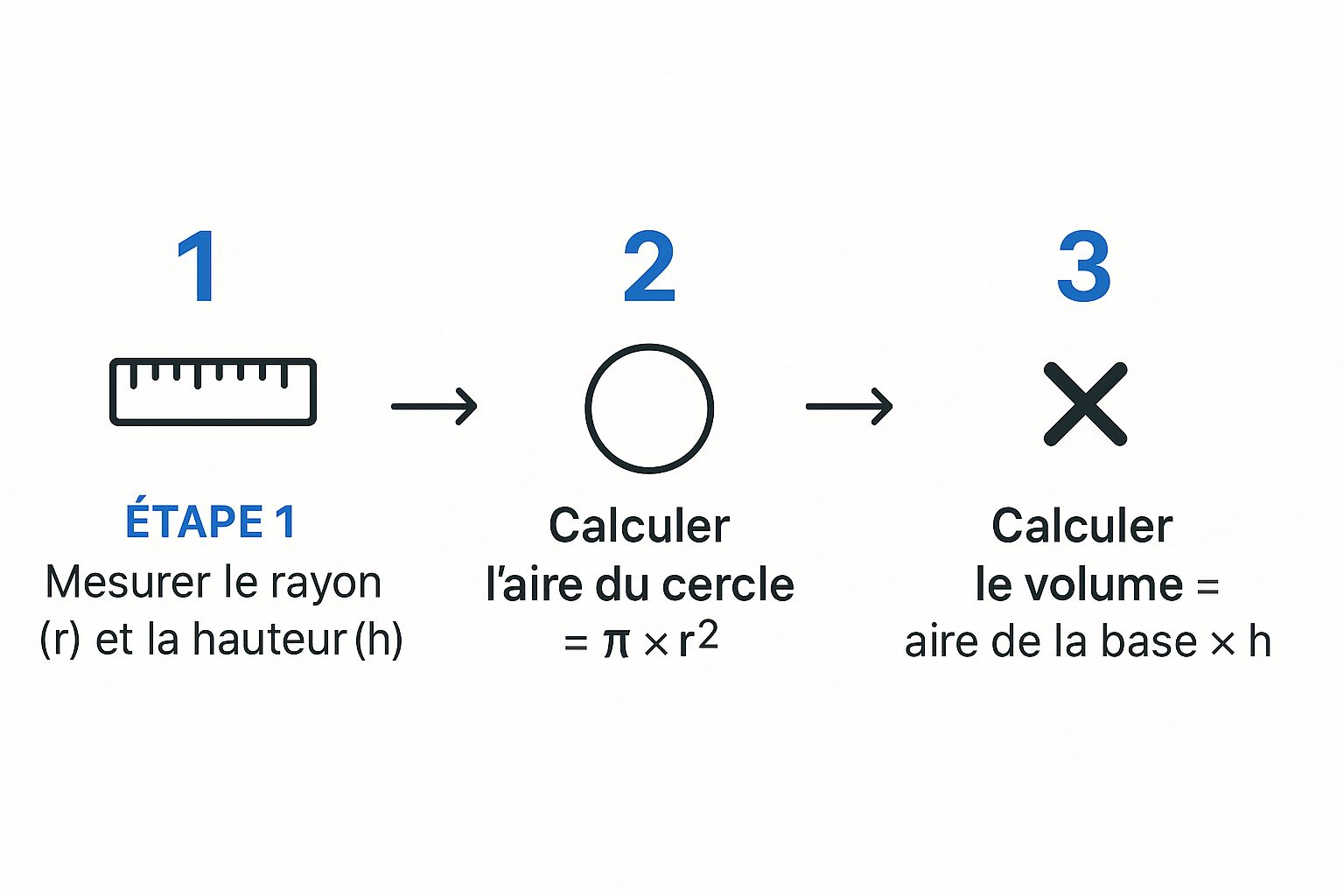
Comme vous pouvez le voir, tout commence par des mesures fiables du rayon et de la hauteur. En prenant le temps de bien identifier ces deux valeurs dès le départ, vous mettez toutes les chances de votre côté pour que le reste du calcul se déroule sans accroc.
La logique derrière la formule V = πr²h
Comprendre pourquoi une formule fonctionne est souvent bien plus utile que de simplement la mémoriser. Pour calculer le volume d’un cylindre, la formule V = πr²h peut sembler abstraite au premier abord, mais elle repose sur une idée très simple et visuelle.

Imaginez votre cylindre comme une pile de crêpes parfaitement identiques. Chaque crêpe représente la base circulaire de votre objet. La formule commence donc par calculer la surface d’une seule de ces crêpes, ce qui correspond à l'aire de la base.
C’est précisément ce que fait la première partie de la formule, πr². Elle ne sert qu'à mesurer l'aire du cercle qui forme le fond (ou le dessus) du cylindre.
Empiler les surfaces pour créer le volume
Une fois que vous avez l’aire de cette tranche de base, la deuxième étape du calcul, la multiplication par la hauteur (h), entre en jeu. En multipliant l'aire de la base par la hauteur, vous faites quelque chose de très concret : vous empilez conceptuellement ces disques circulaires les uns sur les autres, jusqu'à atteindre le sommet du cylindre.
C’est cet empilement qui remplit l’espace tridimensionnel et vous donne le volume total. Autrement dit, chaque centimètre de hauteur ajoute une nouvelle « couche » de volume, dont la taille est égale à l'aire de la base.
L’idée est de transformer un calcul en 2D (l’aire d’un cercle) en une mesure 3D (le volume) simplement en « étirant » cette surface vers le haut. C'est comme si vous preniez une feuille de papier circulaire et que vous l'éleviez pour voir tout l'espace qu'elle occupe en hauteur.
Prenons l'exemple concret d'une cuve de récupération d'eau de pluie. Si sa base a un rayon de 50 cm et sa hauteur est de 120 cm, le calcul se déroule ainsi :
- Aire de la base : π × (50 cm)² ≈ 7 854 cm²
- Volume total : 7 854 cm² × 120 cm = 942 480 cm³
Cette logique s'applique partout, des petites boîtes de conserve aux immenses réservoirs industriels. Le calcul du volume d’un cylindre est d’ailleurs essentiel dans plusieurs domaines. Par exemple, pour un cylindre avec un rayon de 7 cm et une hauteur de 10 cm, son volume serait de V = 3,14159 × 7² × 10 ≈ 1 539 cm³, soit un peu plus de 1,5 litre.
Si le volume mesure l'espace intérieur, il est parfois tout aussi important de connaître la surface extérieure de l'objet. Pour aller plus loin, notre guide sur le calcul de l'aire d'un cylindre vous montrera comment mesurer la surface totale de votre objet.
Le calcul du volume d’un cylindre, une compétence utile au quotidien
Loin d’être une simple formule perdue dans un manuel de maths, savoir calculer le volume d’un cylindre est une compétence étonnamment pratique. Vous seriez surpris de voir à quel point ce calcul s’immisce dans notre quotidien, souvent de manière invisible, mais essentielle au fonctionnement de bien des choses.

Prenez le domaine de l’ingénierie civile, par exemple. Les ingénieurs s’en servent constamment pour concevoir des réservoirs d’eau, des silos à grains ou des citernes de camion. La capacité de stockage de ces structures doit être calculée avec précision pour garantir leur efficacité et leur sécurité.
Plus près de nous, dans notre propre cour, un paysagiste doit calculer la quantité de terre nécessaire pour remplir un grand pot de fleurs cylindrique. Ce simple calcul permet d’éviter le gaspillage et d’économiser temps et argent.
Des exemples concrets et variés
Mais les applications ne s’arrêtent pas là. La formule du volume d’un cylindre est cruciale dans des domaines aussi variés que la mécanique et même la gestion de l’environnement.
- En mécanique automobile : La fameuse « cylindrée » d’un moteur, qui influence directement sa puissance, correspond tout simplement au volume total des cylindres qui le composent.
- Dans l'industrie alimentaire : Les fabricants de conserves ou de boissons gazeuses se basent sur ce calcul pour standardiser le remplissage de millions de canettes chaque jour.
- Pour les amateurs d’aquariums : Déterminer la bonne quantité de sable pour le fond d’un aquarium cylindrique revient à calculer le volume d’une fine couche en forme de cylindre.
Cette compétence mathématique guide même des décisions importantes dans la gestion des ressources. Dans les régions sujettes aux sécheresses, calculer le volume des réservoirs d’eau est vital. Un grand réservoir de 20 mètres de diamètre et 15 mètres de haut peut contenir plus de 4 700 mètres cubes d'eau, une information capitale pour la planification.
Chaque fois que vous suivez une recette qui demande une certaine quantité de liquide dans une casserole, vous utilisez sans le savoir le concept de volume. Votre casserole est un cylindre, et sa capacité est une application directe de cette formule.
La géométrie n’est évidemment pas limitée aux cylindres. Si vous êtes curieux de savoir comment aborder d’autres formes en 3D, notre guide sur le volume d'un cône est un excellent point de départ pour aller plus loin.
Éviter les pièges courants lors du calcul
Même avec la bonne formule en main pour calculer le volume d’un cylindre, il y a quelques erreurs classiques qui peuvent facilement fausser votre résultat. En les connaissant, vous pouvez les anticiper et garantir que vos calculs sont justes à chaque fois.
L'erreur la plus fréquente, et de loin, c'est la confusion entre le rayon et le diamètre. C'est un grand classique. Si votre mesure initiale est le diamètre du cercle, vous devez impérativement le diviser par deux avant de l'intégrer à la formule. Si vous oubliez cette étape, vous obtiendrez un volume quatre fois plus grand que la réalité. Imaginez la différence sur un projet de construction!
La cohérence des unités de mesure
Un autre piège bien connu, c'est le mélange des unités. Disons que vous mesurez la hauteur en mètres et le rayon en centimètres. Le résultat final n'aura tout simplement aucun sens. Assurez-vous que toutes vos mesures sont dans la même unité avant même de commencer.
L'astuce est simple : choisissez une seule unité (cm, m, etc.) et convertissez toutes vos mesures dans cette unité avant de toucher à votre calculatrice. C'est une petite étape de préparation qui vous sauvera bien des maux de tête.
Si vous avez besoin d'un coup de main pour ça, notre guide sur la conversion de mesure est une ressource précieuse pour uniformiser vos données sans vous tromper.
Enfin, il y a la question de la précision de Pi (π) et de l'arrondi final. Utiliser 3,14 est souvent suffisant pour des estimations rapides. Par contre, pour un calcul qui demande plus de précision, il vaut mieux utiliser la touche π de votre calculatrice. Arrondissez votre réponse finale de manière logique, généralement à deux décimales, à moins qu'on vous demande une précision différente.
Cette rigueur est cruciale dans des domaines comme la mécanique, où la cylindrée d'un moteur se calcule avec cette même formule. En Californie, par exemple, le calcul du volume de chaque cylindre d'un moteur est essentiel pour respecter les réglementations environnementales. C'est un bon exemple qui montre à quel point un calcul précis est important dans le monde réel. Vous pouvez d'ailleurs en apprendre plus sur l'application de cette formule en ingénierie automobile.
Foire aux questions sur le volume du cylindre
Même quand on pense maîtriser la formule, certaines questions peuvent encore nous trotter dans la tête. Passons en revue les interrogations les plus fréquentes pour être sûr que tout est bien clair.
Et si mon cylindre est penché?
Un cylindre incliné, qu'on appelle aussi cylindre oblique, peut avoir l'air plus intimidant. Pourtant, la formule V = πr²h ne change absolument pas.
La seule chose à retenir, c'est que la hauteur (h) doit toujours être la hauteur perpendiculaire. C'est la distance bien droite entre les deux bases, pas la longueur du côté qui est penché.
Comment je fais si j'ai seulement la circonférence?
Si on vous donne la circonférence (C) de la base mais pas le rayon, pas de souci. Il suffit de faire un petit détour par la formule de la circonférence, C = 2πr, pour isoler le rayon.
Ça nous donne : r = C / (2π). Une fois que vous avez cette valeur, vous n'avez plus qu'à la glisser dans la formule du volume.
L'important, c'est de toujours revenir aux deux piliers de la formule : le rayon et la hauteur. Peu importe les données de départ, votre première mission est de trouver ces deux mesures avant de faire le calcul final.
Comment obtenir un calcul plus précis?
Pour des résultats fiables, la précision est la clé. Un petit truc simple : utilisez toujours la touche π de votre calculatrice au lieu de l'approximation 3,14. C'est beaucoup plus exact.
Évidemment, assurez-vous aussi que vos mesures de départ sont les plus justes possible. Pour aller plus loin et vraiment optimiser votre façon de travailler en maths, il existe des astuces pour savoir comment étudier efficacement et aborder n'importe quel problème avec plus de confiance.
Si les formules mathématiques restent un défi, Centrétudes propose un accompagnement personnalisé pour transformer les obstacles en réussites. Visitez notre site pour trouver le tuteur idéal : https://centretudes.ca.


