Pour vraiment comprendre comment additionner des fractions, il faut d'abord visualiser ce qu'elles représentent. Le plus simple, c'est d'imaginer une pizza. Le chiffre du bas, qu'on appelle le dénominateur, nous dit en combien de parts égales la pizza est coupée. Celui du haut, le numérateur, indique simplement combien de ces parts on a devant nous.
Pourquoi bien comprendre les fractions est essentiel avant de les additionner
Essayer d’additionner des fractions sans avoir cette image en tête, c'est un peu comme vouloir construire une maison sans fondations solides. Ça ne tient pas la route. Chaque chiffre dans une fraction a un rôle bien précis, et si on l'ignore, on fonce droit vers l'erreur.
Le rôle de chaque chiffre
Le numérateur et le dénominateur ne sont pas juste deux chiffres l'un sur l'autre; ils forment une équipe. Le dénominateur, c'est la « taille » de la part, sa catégorie. C'est pour ça qu'on ne peut pas additionner directement des parts de tailles différentes, comme des quarts (1/4) et des tiers (1/3).
Pensez-y : vous avez une part d'un gâteau coupé en quatre et une autre d'un gâteau coupé en trois. Mettre les deux ensemble ne donne pas un résultat logique, car les morceaux ne sont pas pareils. La toute première étape est donc toujours de les rendre comparables. Une fois qu'on a compris ça, les règles mathématiques deviennent intuitives et cessent d'être de simples formules à mémoriser.
Maîtriser le rôle du numérateur et du dénominateur transforme l'addition de fractions. Ça passe d'un exercice de mémorisation à une application logique et concrète de la pensée.
Ce concept, pourtant fondamental, est un défi bien connu dans l'enseignement. Une étude de 2019 de l'Université de Californie a montré qu'environ 34 % des élèves du collège avaient encore du mal avec l'addition de fractions, souvent à cause d'une mauvaise compréhension de ces notions de base. C'est un chiffre qui peut sembler élevé, mais c'est une nette amélioration par rapport aux 60 % des années 1980, en grande partie grâce à l'utilisation d'outils visuels comme la pizza!
Si votre enfant bute sur ces concepts, un petit coup de pouce peut faire toute la différence. Découvrez comment le tutorat en mathématiques peut l'aider à bâtir une confiance solide et durable.
Additionner des fractions : le cas facile des dénominateurs identiques
Commençons par le scénario le plus simple, celui qui rend l’addition de fractions beaucoup plus intuitive. C'est le cas où les deux fractions que vous souhaitez additionner ont exactement le même dénominateur, c'est-à-dire le même chiffre du bas.
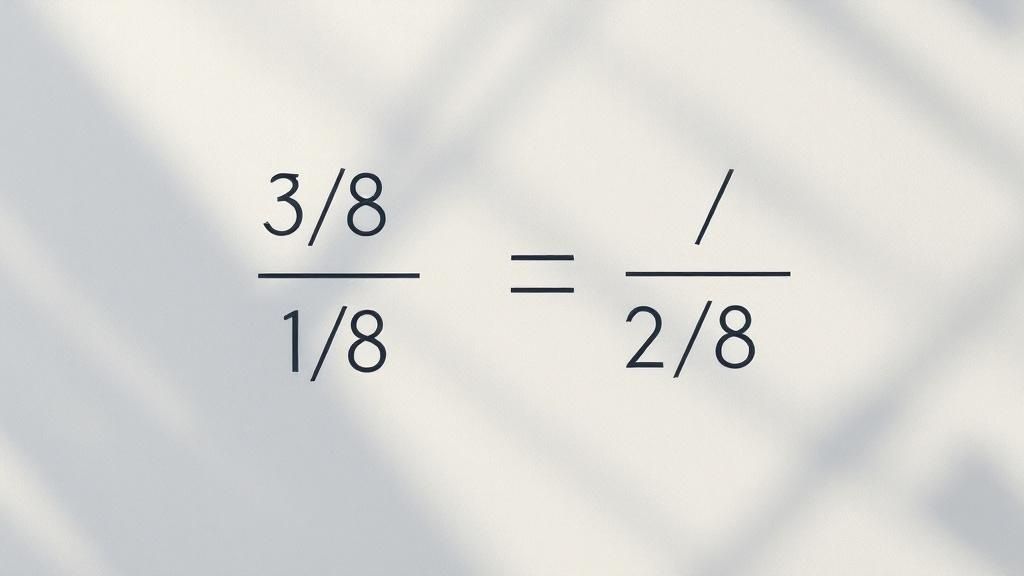
Pensez à une pizza coupée en 8 parts égales. Si vous en avez déjà 2/8 et que quelqu'un vous en offre 3/8 de plus, vous comprenez instinctivement que vous possédez maintenant 5 parts sur 8 au total.
Le calcul est tout aussi direct : 2/8 + 3/8 = 5/8. La logique est simple : la taille de chaque part (le dénominateur) ne change pas; seul le nombre de parts que vous possédez (le numérateur) augmente.
La règle d'or pour les dénominateurs communs
La seule règle à retenir ici est d'additionner les numérateurs (les chiffres du haut) et de conserver le dénominateur tel quel. Il reste inchangé parce qu'il définit l'unité de mesure commune, la taille des « morceaux » que vous comptez.
Voici quelques exemples concrets pour illustrer ce principe :
- En cuisine : Si vous mélangez 1/4 de tasse de farine avec 2/4 de tasse, vous obtenez 3/4 de tasse. Le calcul est simple : 1/4 + 2/4 = (1+2)/4 = 3/4.
- En randonnée : Un parcours est divisé en dix sections. Si vous parcourez 3/10 du chemin avant midi et 5/10 après, vous avez fait 3/10 + 5/10 = 8/10 du trajet total.
La clé, c'est de ne jamais, au grand jamais, additionner les dénominateurs entre eux. Considérez-le comme le « nom de famille » des fractions : il doit être le même pour que l'addition fonctionne, et il ne change pas dans le résultat final.
Le tableau suivant résume quelques additions simples pour vous aider à visualiser le processus.
Exemples d'addition avec dénominateur commun
| Fraction 1 | Fraction 2 | Résultat intermédiaire | Résultat simplifié |
|---|---|---|---|
| 1/5 | 3/5 | 4/5 | 4/5 |
| 2/6 | 2/6 | 4/6 | 2/3 |
| 5/12 | 1/12 | 6/12 | 1/2 |
| 7/20 | 3/20 | 10/20 | 1/2 |
Comme vous pouvez le voir, parfois le résultat peut être simplifié.
Une fois votre addition terminée, prenez une bonne habitude : vérifiez toujours si votre résultat peut être simplifié. Dans notre exemple de randonnée, 8/10 est une réponse correcte, mais elle peut être réduite. En divisant le numérateur et le dénominateur par 2, on obtient 4/5. Présenter la réponse la plus simple est une marque de rigueur en mathématiques.
Parfois, même avec des calculs simples, il est bon d'avoir un soutien pour solidifier les bases. Pour un accompagnement personnalisé, le tutorat en maths peut aider à transformer ces concepts en réflexes durables.
La technique pour trouver un dénominateur commun
Lorsque les dénominateurs sont différents, l’addition de fractions semble tout de suite plus complexe. Comment peut-on additionner 1/3 et 1/4? C'est le défi le plus courant, mais heureusement, il existe une méthode fiable pour y arriver : trouver un terrain d'entente, ce qu'on appelle un dénominateur commun.
L'idée, c'est de réécrire chaque fraction pour qu'elles partagent la même base, sans changer leur valeur. Pour y parvenir, on utilise une technique simple et efficace : le Plus Petit Commun Multiple (PPCM). Oubliez le jargon mathématique qui peut sembler intimidant; il s'agit simplement de trouver le plus petit nombre qui est un multiple des deux dénominateurs.
Trouver le PPCM pas à pas
Reprenons notre exemple de 1/3 + 1/4. Ici, les dénominateurs sont 3 et 4. Le processus pour identifier le PPCM est assez direct :
- On liste les multiples de chaque dénominateur :
- Multiples de 3 : 3, 6, 9, 12, 15, 18…
- Multiples de 4 : 4, 8, 12, 16, 20…
- On identifie le premier multiple qu'ils ont en commun : En regardant les deux listes, le premier nombre qui apparaît dans les deux est 12. C'est notre PPCM, notre nouveau dénominateur commun!
Cette méthode est fondamentale, car elle vous donne les plus petits chiffres possibles avec lesquels travailler. Ça simplifie grandement les calculs et minimise le risque d'erreurs. Appliquer cette méthode de manière structurée est une excellente habitude à prendre, et pour bien maîtriser cette compétence, il est toujours utile d'apprendre comment bien réviser les étapes clés.
Une fois qu'on a notre dénominateur commun (12), on doit ajuster chaque fraction.
Ajuster les fractions pour qu'elles correspondent
Pour transformer 1/3 en une fraction sur 12, on se pose la question : « Par quoi faut-il multiplier 3 pour obtenir 12 ? ». La réponse est 4. On multiplie donc le numérateur et le dénominateur par ce même chiffre :
- 1/3 devient (1 x 4) / (3 x 4) = 4/12
On fait exactement la même chose pour 1/4. Par quoi multiplier 4 pour arriver à 12? Par 3.
- 1/4 devient (1 x 3) / (4 x 3) = 3/12
L'astuce est de toujours multiplier le haut et le bas par le même nombre. De cette façon, vous changez l'apparence de la fraction, mais pas sa valeur réelle. 1/3 et 4/12 représentent exactement la même quantité.
Maintenant que nos fractions ont le même dénominateur, l'addition devient un jeu d'enfant : 4/12 + 3/12 = 7/12.
Cette infographie résume visuellement le processus pour additionner des fractions avec des dénominateurs différents.

La visualisation montre clairement que trouver le PPCM est l'étape centrale qui transforme un problème qui semble complexe en une simple addition.
Le processus complet pour additionner toutes les fractions
Maintenant que vous avez les bases, mettons tout ça en pratique. On va assembler les pièces du puzzle pour voir comment additionner des fractions concrètement. Vous verrez, une fois qu'on a compris la logique, ça devient un automatisme, peu importe la complexité des chiffres.
Pour bien illustrer les étapes, prenons un exemple très classique que l'on retrouve partout : 2/3 + 3/4.
Transformer les fractions pour qu'elles parlent le même langage
La toute première chose à faire, c'est de trouver un terrain d'entente pour nos dénominateurs, qui sont 3 et 4. On doit donc trouver leur plus petit commun multiple (PPCM). En listant rapidement les multiples, on voit que 12 est le chiffre magique qui va nous permettre de faire le pont entre nos deux fractions.
Maintenant, on convertit chaque fraction pour qu'elle soit sur 12. C'est plus simple qu'il n'y paraît :
- Pour 2/3, la question est : « Par quoi faut-il multiplier 3 pour obtenir 12 ? ». La réponse est 4. On applique donc cette opération en haut et en bas : (2 × 4) / (3 × 4) = 8/12.
- On recommence pour 3/4 : « Par quoi multiplier 4 pour obtenir 12 ? ». Cette fois, c'est 3. On calcule donc : (3 × 3) / (4 × 3) = 9/12.
Le plus difficile est fait ! En transformant 2/3 en 8/12 et 3/4 en 9/12, on a ramené un problème qui semblait compliqué à une simple addition de fractions qui ont le même dénominateur.
Cette étape de conversion est absolument cruciale. C'est là que tout se joue. Une étude de 2023 a d'ailleurs montré qu'environ 72 % des élèves de 5e année maîtrisaient bien ce genre de calcul, car ils avaient vraiment saisi l'importance de ce fameux dénominateur commun. Pour les curieux, vous pouvez en apprendre plus sur la recherche derrière les fractions en mathématiques).
Finaliser l'addition et présenter le résultat
Une fois que nos fractions sont sur le même pied d'égalité, l'addition devient un jeu d'enfant. Il suffit d'additionner les numérateurs entre eux, tout en gardant notre dénominateur commun : 8/12 + 9/12 = 17/12.
Le résultat final est 17/12. C'est ce qu'on appelle une fraction impropre, puisque le numérateur est plus grand que le dénominateur. C'est une réponse parfaitement juste.
En suivant cette méthode bien organisée, vous minimisez les risques d'erreur. Que vous ayez deux, trois ou même plus de fractions à additionner, les étapes restent exactement les mêmes. La clé du succès, c'est de procéder méthodiquement : trouver le PPCM, convertir les fractions, et enfin, additionner.
Mieux comprendre pour ne plus se tromper : conseils pratiques et erreurs fréquentes
Même avec la bonne méthode en tête, il est facile de tomber dans certains pièges classiques lorsqu'on additionne des fractions. Considérez cette section comme votre filet de sécurité pour développer de bons réflexes et vous assurer que chaque calcul est juste.
L'erreur la plus commune, et de loin, est d'additionner les numérateurs ET les dénominateurs. Par exemple, croire que 1/2 + 1/3 est égal à 2/5. C'est une erreur de logique fondamentale. Imaginez : vous ne pouvez pas mélanger des pointes de tarte de différentes grosseurs (des moitiés et des tiers) et prétendre obtenir une nouvelle taille de pointe (des cinquièmes). Ça n'a pas de sens!
Avant même de commencer, prenez l'habitude de vous demander : « Est-ce que mes parts ont la même taille? ». Si la réponse est non, votre toute première mission est claire : trouver un dénominateur commun.
Simplifier avant de commencer : une astuce qui change tout
Un truc souvent oublié, mais terriblement efficace, est de simplifier les fractions avant même de chercher un dénominateur commun. Disons que vous devez additionner 6/12 + 4/8. Vous pourriez vous lancer dans la recherche d'un PPCM qui semble compliqué.
Mais attendez une minute. En simplifiant d'abord, le calcul devient soudainement 1/2 + 1/2, ce qui donne 1. C'est beaucoup plus simple, n'est-ce pas? Travailler avec des chiffres plus petits réduit drastiquement le risque de faire une erreur de calcul.
Voici une petite liste de vérification mentale à adopter :
- Ai-je simplifié toutes mes fractions au maximum avant de commencer?
- Mon dénominateur commun est-il vraiment le plus petit multiple possible (le fameux PPCM)?
- Ai-je bien pensé à multiplier le numérateur par le même chiffre que son dénominateur?
Prendre deux secondes pour valider ces points peut vous sauver bien des maux de tête. C'est en développant de bonnes habitudes de travail que les maths deviennent plus faciles, ce qui souligne l'importance des devoirs pour que ces gestes deviennent des automatismes.
Enfin, n'hésitez pas à vous aider d'outils interactifs. Une étude a même montré que 72 % des élèves qui utilisent des supports visuels obtiennent de meilleurs résultats. Pour aller plus loin, vous pouvez consulter ces ressources sur l'addition des fractions qui pourraient bien vous aider à visualiser le tout.
On répond à vos questions sur l'addition des fractions
Même avec le meilleur guide du monde, il reste parfois quelques zones d'ombre. C'est tout à fait normal! Démystifions ensemble les derniers points pour que l'addition de fractions n'ait plus aucun secret pour vous.
Pourquoi est-ce qu'on n'additionne jamais les dénominateurs?
Pensez à une pizza. Le dénominateur, c'est le nombre total de pointes dans lesquelles elle est coupée. Si vous avez une moitié (1/2) et un ami a un tiers (1/3), vous ne pouvez pas simplement additionner les dénominateurs (2+3). Vos pointes n'ont pas la même taille!
Pour savoir combien de pizza vous avez en tout, vous devez d'abord "recouper" les deux pizzas virtuellement en pointes de taille identique. C'est ça, trouver un dénominateur commun. Une fois que toutes les pointes sont égales, là, vous pouvez enfin les compter en additionnant les numérateurs.
Comment faire pour additionner un nombre entier et une fraction?
C'est plus simple qu'il n'y paraît. La technique la plus directe est de transformer le nombre entier en fraction.
Prenons l'exemple de 3 + 1/4. Il suffit d'exprimer le 3 en quarts. Puisque chaque unité contient quatre quarts, 3 unités en contiennent douze (12/4). L'opération devient alors une simple addition de fractions qui ont déjà le même dénominateur : 12/4 + 1/4 = 13/4. Et voilà!
Un petit conseil d'expert : même si ce n'est pas obligatoire, essayez toujours d'utiliser le plus petit dénominateur commun (le PPCM). Ça vous évite de jongler avec de grands nombres et, bien souvent, ça vous sauve l'étape de simplification à la fin. C'est un réflexe qui rend les calculs beaucoup plus fluides.
Au-delà des mathématiques, une bonne maîtrise du français est tout aussi cruciale pour la réussite scolaire. Pour varier les plaisirs, n'hésitez pas à faire un exercice sur les participes passés pour garder vos compétences à jour.
Si votre enfant a besoin d'un coup de pouce pour transformer ses difficultés en confiance, Centrétudes offre un accompagnement personnalisé en mathématiques et bien plus. Découvrez nos services sur https://centretudes.ca.


