Diviser des fractions, ça se résume à une petite astuce mathématique : on transforme la division en multiplication en utilisant l’inverse de la deuxième fraction. C'est une technique qui simplifie grandement un calcul qui, à première vue, peut paraître compliqué.
Pourquoi diviser des fractions semble si difficile
Soyons honnêtes, la division de fractions intimide beaucoup de monde. Que ce soit sur les bancs d'école ou des années plus tard, cette opération traîne une réputation de casse-tête arithmétique. Mais pourquoi cette idée est-elle si tenace?
Le piège de l'intuition
Le premier obstacle est purement intuitif. Notre cerveau, habitué à jongler avec des nombres entiers, essaie d'appliquer la même logique partout. Quand on voit une opération comme 3/4 ÷ 1/2, le réflexe est souvent de vouloir diviser les numérateurs entre eux (3 ÷ 1) et les dénominateurs entre eux (4 ÷ 2). Cette approche est non seulement fausse, mais elle conduit à des résultats complètement à côté de la plaque.
Cette difficulté n'est d'ailleurs pas un cas isolé. Une étude internationale a montré que le niveau en mathématiques des élèves québécois, notamment sur les opérations de base comme les fractions, a tendance à stagner. Bien que le Québec se démarque souvent, ces concepts fondamentaux restent un défi pour plusieurs. Maîtriser ces bases est donc essentiel. Pour en savoir plus, vous pouvez consulter cette analyse sur le site de Radio-Canada.
Le concept clé qui fait toute la différence
En réalité, la difficulté n’est pas tant dans le calcul lui-même que dans la compréhension d'un concept un peu abstrait : la notion d'« inverse ». Diviser, ce n'est pas juste partager en parts plus petites. Diviser par une fraction, c’est se demander : « Combien de fois cette fraction rentre-t-elle dans mon nombre de départ? »
Pensez-y de cette façon : diviser par 1/2, c’est chercher combien de « moitiés » on peut trouver dans un tout. La réponse est deux. Et ça correspond au résultat de la multiplication par 2, qui est l'inverse de 1/2. C'est ce petit changement de perspective qui est la clé.
Une fois qu'on a ce déclic, diviser des fractions perd son aura de mystère. L'opération devient une simple multiplication, une compétence qu'on maîtrise généralement déjà bien. C'est aussi un excellent exercice pour aiguiser son raisonnement logique, bien au-delà des maths. D'ailleurs, une bonne connaissance des règles de base peut vraiment simplifier les choses. Si vous voulez vous rafraîchir la mémoire, notre guide sur les critères de divisibilité est un excellent point de départ.
La méthode infaillible pour la division de fractions
Entrons dans le vif du sujet. La division de fractions peut sembler intimidante, mais elle repose sur une règle d'or, une astuce si simple qu'elle transforme un problème potentiellement complexe en une simple multiplication.
Retenez bien cette phrase, car elle est la clé de tout : diviser par une fraction, c’est multiplier par son inverse.
Cette méthode est à la fois élégante et directe. Elle consiste à prendre la deuxième fraction de l'opération (celle qui divise) et à simplement échanger son numérateur (le chiffre du haut) avec son dénominateur (le chiffre du bas). Une fois cette fraction « inversée », on remplace le signe de division (÷) par un signe de multiplication (×). Et le tour est joué!
Le processus expliqué simplement
Visualisons cela avec un exemple classique pour bien comprendre comment diviser des fractions comme 1/2 ÷ 3/4.
On commence par conserver la première fraction telle quelle. Dans notre cas, 1/2 reste inchangée. On ne touche jamais à celle-ci.
Ensuite, on inverse la deuxième fraction. La fraction 3/4 devient donc 4/3. C'est l'étape cruciale.
Puis, on change le signe de l'opération. Le signe de division (÷) se transforme en un signe de multiplication (×).
Finalement, on multiplie les deux nouvelles fractions. On multiplie les numérateurs ensemble (1 × 4 = 4) et les dénominateurs ensemble (2 × 3 = 6). On obtient 4/6, qui se simplifie en 2/3.
L'infographie ci-dessous illustre parfaitement ce processus.
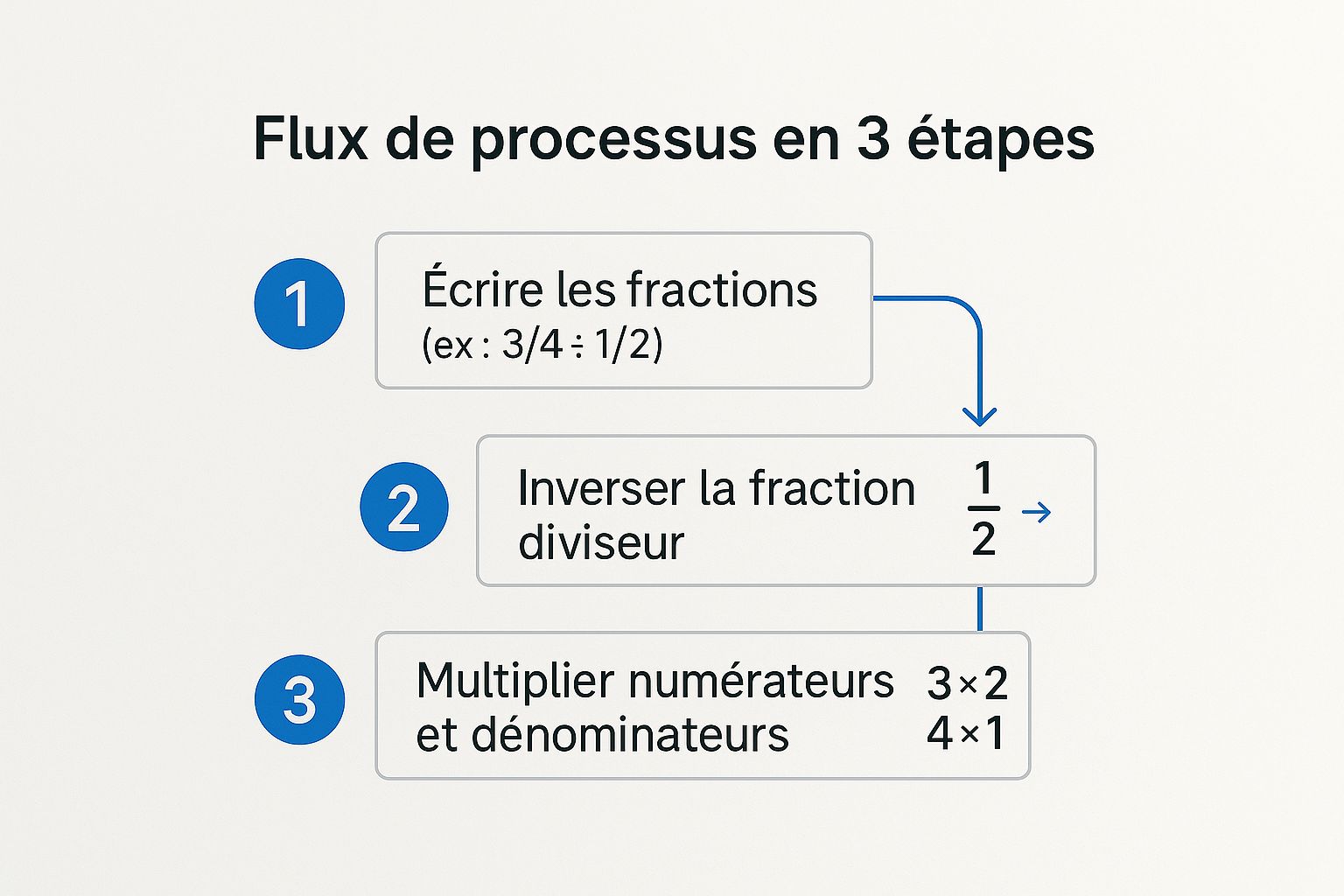
Ce visuel montre bien que l'inversion de la deuxième fraction est le geste qui débloque tout le calcul.
Pour résumer visuellement cette technique, voici un tableau qui décompose le processus.
Transformer la division en 3 étapes simples
Ce tableau montre comment transformer n'importe quel problème de division de fractions en une multiplication beaucoup plus facile à gérer.
| Étape | Action à réaliser | Exemple avec (a/b) ÷ (c/d) |
|---|---|---|
| 1. Garder | Conserver la première fraction sans la modifier. | On garde (a/b). |
| 2. Inverser | Inverser le numérateur et le dénominateur de la deuxième fraction. | (c/d) devient (d/c). |
| 3. Multiplier | Changer le signe de division (÷) par un signe de multiplication (×). | On calcule (a/b) × (d/c). |
En suivant ces trois actions – garder, inverser, multiplier –, vous avez une méthode fiable pour résoudre n'importe quelle division de fractions.
La règle à mémoriser : Pour diviser (a/b) par (c/d), il suffit de calculer (a/b) × (d/c). C’est le seul principe dont vous avez besoin pour réussir toutes vos divisions de fractions.
Cette technique est universelle. Elle fonctionne que les fractions soient simples, complexes ou même accompagnées de nombres entiers. C'est pourquoi sa maîtrise est si importante. Pour approfondir votre compréhension de la division des fractions avec d'autres exemples, n'hésitez pas à explorer notre guide détaillé.
Adopter ce réflexe « inverser et multiplier » est le chemin le plus sûr pour ne plus jamais être bloqué par ce type d'opération. La pratique régulière ancrera cette méthode, la rendant aussi naturelle que n'importe quelle autre multiplication.
Mettre la méthode en pratique avec des exemples concrets
La théorie, c’est bien, mais rien ne vaut la pratique pour vraiment maîtriser une compétence. C'est en appliquant concrètement la méthode « inverser et multiplier » à différents scénarios que les mécanismes deviendront un véritable réflexe.
Commençons en douceur avec des cas simples pour bâtir des fondations solides avant d'aborder des problèmes plus costauds.

Un exemple de base pour commencer
Prenons une division de fractions toute simple : 2/5 ÷ 1/3.
La première étape, c'est de ne pas toucher à la première fraction. On la garde telle quelle. Ensuite, on prend la deuxième fraction, 1/3, et on l'inverse. Ça nous donne 3/1. Et pour finir, on remplace le signe de division par une multiplication.
Le calcul se transforme donc en : 2/5 × 3/1.
Maintenant, il suffit de multiplier les numérateurs ensemble (2 × 3 = 6) et les dénominateurs ensemble (5 × 1 = 5). Le résultat final est 6/5. Comme 6 et 5 n'ont pas de diviseur commun, la fraction est déjà à sa plus simple expression. C'est ce qu'on appelle une fraction irréductible.
Comment gérer la division par un nombre entier
Que faire si on doit diviser une fraction par un nombre entier, comme dans 4/7 ÷ 5? C'est une situation courante, et l'astuce est toute simple. Il faut se rappeler que n'importe quel nombre entier peut s'écrire comme une fraction en le plaçant sur un dénominateur de 1.
Donc, notre 5 devient 5/1. Le problème se réécrit alors : 4/7 ÷ 5/1.
À partir de là, on applique notre règle habituelle : on conserve 4/7, on inverse 5/1 pour obtenir 1/5, et on change le signe pour une multiplication.
Le calcul devient : 4/7 × 1/5.
Le résultat est (4 × 1) / (7 × 5), ce qui nous donne 4/35. La réponse est déjà simplifiée, pas besoin d'aller plus loin.
Cette technique marche aussi dans l'autre sens, bien sûr. Par exemple, pour 8 ÷ 2/3. On transforme 8 en 8/1, on inverse 2/3 en 3/2, et on calcule 8/1 × 3/2 = 24/2, qui se simplifie pour donner 12.
Le truc à retenir : Un nombre entier est simplement une fraction avec un dénominateur de 1. Cette petite transformation vous permet d'utiliser la même méthode à tous les coups, sans jamais avoir à apprendre de nouvelle règle.
Aborder les nombres fractionnaires
Les choses se corsent un peu avec les nombres fractionnaires (aussi appelés nombres mixtes), comme dans 2 ½ ÷ 1 ¼. La première étape, et elle est indispensable, c'est de convertir ces nombres en fractions impropres.
- Pour 2 ½, on calcule (2 × 2) + 1 = 5. Le dénominateur, lui, ne change pas. La fraction est donc 5/2.
- Pour 1 ¼, même principe : (1 × 4) + 1 = 5. Le dénominateur reste 4. On obtient 5/4.
Notre opération de départ est maintenant devenue 5/2 ÷ 5/4.
On peut maintenant appliquer notre méthode favorite. On garde 5/2, on inverse 5/4 en 4/5, et on multiplie : 5/2 × 4/5.
Le résultat est (5 × 4) / (2 × 5), ce qui donne 20/10. Cette fraction se simplifie très facilement pour donner 2.
Cette approche progressive, en partant des cas simples pour aller vers des exemples plus complexes, est la meilleure façon de renforcer sa confiance. Chaque problème, qu'il implique des nombres entiers ou fractionnaires, repose sur la même logique fondamentale. C'est ça, la beauté des maths
Les erreurs courantes à éviter à tout prix
Maitriser la division de fractions, c’est bien. Savoir déjouer les pièges classiques, c’est encore mieux pour être vraiment sûr de soi. En identifiant ces petites erreurs fréquentes, vous développerez de bien meilleurs réflexes pour vérifier vos calculs.
L’erreur la plus commune? Inverser la mauvaise fraction. Dans le feu de l'action, on peut facilement retourner la première fraction au lieu de la seconde. Gardez toujours en tête que c’est le diviseur (la deuxième fraction) qui s'inverse, jamais la première.
Un autre oubli très fréquent est d’inverser la fraction, mais de conserver le signe de division. Or, la méthode fonctionne uniquement si vous faites les deux changements en même temps : inverser la deuxième fraction ET remplacer le signe de division (÷) par une multiplication (×). C’est un duo inséparable.
La simplification hâtive, un faux ami
Simplifier les fractions est une excellente habitude, mais attention au timing! Le faire trop tôt peut complètement fausser votre réponse. Il est souvent tentant de simplifier dès le début, avant même d'avoir transformé la division en multiplication.
Astuce pratique : Attendez toujours d'avoir réécrit le problème comme une multiplication avant de simplifier quoi que ce soit. Par exemple, pour 5/4 ÷ 15/8, ne touchez à rien. Une fois que vous avez 5/4 × 8/15, là, vous pouvez simplifier en croix.
Cette petite discipline vous évitera bien des maux de tête. La rigueur dans l'ordre des opérations est la clé du succès, et pas seulement pour les fractions. Savoir additionner des fractions, par exemple, demande une logique d'étapes tout aussi précise, comme nous l'expliquons dans notre guide sur comment additionner des fractions.
Comprendre ces concepts fondamentaux est crucial. Malheureusement, les difficultés en mathématiques peuvent s’installer très tôt et créer des écarts qui perdurent. En prenant conscience de ces pièges, vous vous donnez les moyens de surmonter plus facilement les obstacles.
Quand utiliser la division de fractions dans la vraie vie
Contrairement à ce qu'on pourrait penser, les mathématiques ne sont pas qu'une matière abstraite confinée aux salles de classe. C'est un outil incroyablement pratique qui nous aide à résoudre des problèmes très concrets. La division de fractions, par exemple, s'invite dans notre quotidien bien plus souvent qu'on ne l'imagine, surtout quand la précision est de mise.

Pensez à votre recette de biscuits préférée, celle qui donne 24 délicieux biscuits. Aujourd'hui, vous n'en voulez que la moitié, soit 12. La recette indique ¾ de tasse de sucre. Pour ajuster les proportions, il faut tout simplement diviser cette quantité par deux : ¾ ÷ 2. Voilà, le tour est joué!
Du bricolage à la couture
Ce même raisonnement s'applique à une foule de projets manuels. Vous avez une belle planche de bois de 1 ½ mètre et votre projet nécessite des morceaux de ¼ de mètre. Pour savoir combien de sections vous pouvez obtenir, le calcul est simple : 1 ½ ÷ ¼.
Le résultat de cette opération est sans équivoque : vous obtiendrez exactement six morceaux, sans la moindre retaille. La division de fractions transforme ainsi une simple estimation en une certitude mathématique.
Une couturière qui doit tailler des rubans de ⅓ de mètre à partir d'un rouleau de 5 mètres se servira du même calcul pour éviter le gaspillage et optimiser son tissu. Ces compétences sont fondamentales dans bien des métiers, qu'ils soient techniques ou créatifs.
Les occasions de partager équitablement des quantités qui ne sont pas des nombres ronds sont partout autour de nous. De la planification d'un projet au partage d'une pizza entre amis, la division de fractions est un superpouvoir pour la vie de tous les jours. Si ces notions vous semblent encore un peu floues, un coup de pouce peut tout changer. Découvrez comment nos services de tutorat en mathématiques aident les élèves à maîtriser ces compétences et à les appliquer avec confiance.
Vos questions sur la division de fractions
Même avec la meilleure méthode en main, certaines questions reviennent souvent. C'est tout à fait normal! Cette section est là pour faire la lumière sur ces derniers points et vous donner une confiance totale face à n'importe quelle division de fractions.
Pourquoi doit-on inverser la deuxième fraction et pas la première?
Voilà une excellente question qui va droit au cœur de l'opération. En mathématiques, diviser par un nombre, c'est la même chose que de multiplier par son inverse. La deuxième fraction, qu’on appelle le diviseur, est celle qui « fait » l'action de diviser. C’est donc son rôle qu’on transforme en une multiplication.
Si on inversait la première fraction, on changerait complètement le sens du problème et le résultat serait faux. C'est un peu comme si dans la phrase « le chat poursuit la souris », on décidait soudain que c'est la souris qui poursuit le chat. L'ordre et le rôle de chaque élément sont essentiels!
Comment faire si je dois diviser plus de deux fractions?
Pas de panique si vous tombez sur une chaîne de divisions comme (1/2) ÷ (3/4) ÷ (2/5). La règle d’or est de procéder de gauche à droite, une seule opération à la fois. Surtout, n'essayez pas de tout inverser d'un seul coup.
- Occupez-vous de la première division : (1/2) ÷ (3/4).
On applique la règle : (1/2) × (4/3), ce qui nous donne 4/6. Simplifié, ça devient 2/3. - Continuez avec ce nouveau résultat : Le problème est maintenant devenu (2/3) ÷ (2/5).
On recommence : (2/3) × (5/2). Le résultat est 10/6, qui se simplifie en 5/3.
En y allant étape par étape, on garde le contrôle et on évite de s'emmêler les pinceaux.
Le conseil du pro
Pour ne pas vous perdre, réécrivez le calcul à chaque étape. Une fois la première division résolue, votre nouvelle ligne de calcul doit commencer par le résultat que vous venez de trouver. C'est une méthode simple, mais incroyablement efficace pour prévenir les erreurs d'inattention.
Puis-je simplifier les fractions avant de multiplier?
Absolument! C'est même une habitude géniale à prendre. Cette technique, qu'on appelle parfois la « simplification en croix », vous permet de travailler avec des chiffres beaucoup plus petits. Le calcul final devient alors un jeu d'enfant.
Attention, il y a une seule condition : cette simplification ne peut se faire qu'après avoir transformé la division en multiplication.
Prenons un exemple concret : 8/9 ÷ 4/3.
L'opération devient d'abord 8/9 × 3/4.
Maintenant, on peut simplifier en diagonale.
- Le 8 (en haut) et le 4 (en bas) sont tous les deux divisibles par 4.
- Le 3 (en haut) et le 9 (en bas) sont tous les deux divisibles par 3.
Votre calcul, une fois simplifié, ressemble à ceci : 2/3 × 1/1. Le résultat est instantané : 2/3. C'est bien plus rapide que de calculer 24/36 pour ensuite devoir le simplifier. Pour mieux comprendre la logique mathématique appliquée à d'autres domaines, un tutorat en sciences peut offrir des éclaircissements vraiment précieux.
Avoir les bonnes réponses à ces questions, c’est un pas de plus vers la maîtrise. Chez Centretudes, nous croyons qu'aucune question n'est trop simple et que chaque éclaircissement renforce la confiance. Découvrez comment nous pouvons aider votre enfant en visitant notre site https://centretudes.ca.


