La circonférence d'un cercle, qu'est-ce que c'est au juste? C'est tout simplement la mesure de son contour. Pensez-y comme la longueur totale de la ligne qui dessine le cercle.
Imaginez que vous prenez une roue de vélo et que vous la déroulez jusqu'à former une ligne droite. La longueur de cette ligne, c'est précisément sa circonférence.
Les bases du calcul de la circonférence
Avant de sauter dans les formules, il faut bien comprendre que la circonférence n'est pas qu'un concept abstrait de mathématiques. C'est une mesure bien réelle qu'on retrouve partout autour de nous, du bord d'une simple tasse de café aux immenses structures comme une grande roue.
Pour la calculer, on n'a besoin que d'une seule de ces deux informations :
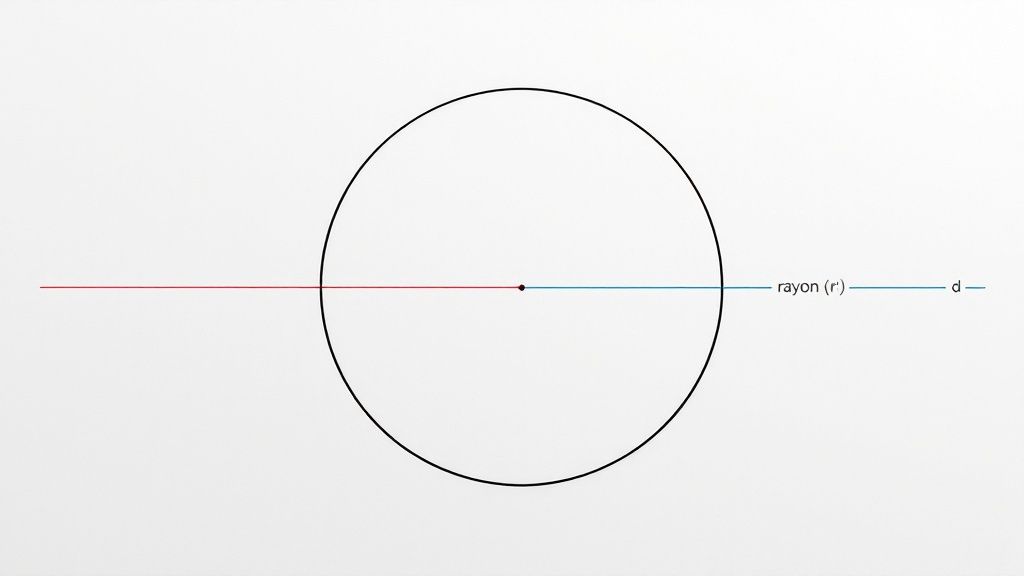
- Le rayon (r) : C'est la distance qui part du centre du cercle pour aller jusqu'à n'importe quel point sur son bord.
- Le diamètre (d) : C'est la distance qui traverse le cercle d'un bord à l'autre, en passant pile par le centre. Il est toujours exactement le double du rayon (d = 2r).
Une fois que vous avez l'une de ces deux mesures en main, le reste devient un jeu d'enfant grâce à une constante mathématique aussi célèbre que fascinante : Pi (π).
Les deux formules essentielles à connaître
Peu importe la taille d'un cercle, qu'il soit minuscule ou gigantesque, le rapport entre sa circonférence et son diamètre reste toujours le même. Cette constante, c'est le fameux nombre Pi (π), qui vaut approximativement 3,14159. C'est grâce à cette incroyable régularité qu'on peut utiliser deux formules simples et puissantes.
Le calcul de la circonférence s'appuie principalement sur la formule C = 2πr. Ici, C est la circonférence, r le rayon, et π la constante. Cette relation directe et proportionnelle entre la taille d'un cercle et son périmètre est la pierre angulaire de nombreux calculs en géométrie et en ingénierie. Si vous souhaitez explorer cette relation plus en profondeur, vous trouverez d'excellentes ressources sur le périmètre du cercle sur maison-des-sciences.org.
Pour visualiser facilement cette formule, voici un tableau qui résume chaque composant.
Les composants clés de la formule
Ce tableau résume les variables de la formule de la circonférence et leurs relations.
| Symbole | Signification | Relation |
|---|---|---|
| C | Circonférence | La longueur totale du contour du cercle. C'est ce qu'on cherche à calculer. |
| r | Rayon | La distance du centre au bord. Il est la moitié du diamètre. |
| d | Diamètre | La distance d'un bord à l'autre en passant par le centre. Il est le double du rayon. |
| π (Pi) | Constante Pi | Le rapport constant (≈ 3,14159) entre la circonférence et le diamètre. |
Ce tableau met en lumière comment chaque élément s'articule pour nous permettre de trouver facilement la circonférence.
L'image ci-dessous illustre parfaitement le lien direct entre le diamètre, la constante Pi et le calcul final de la circonférence.
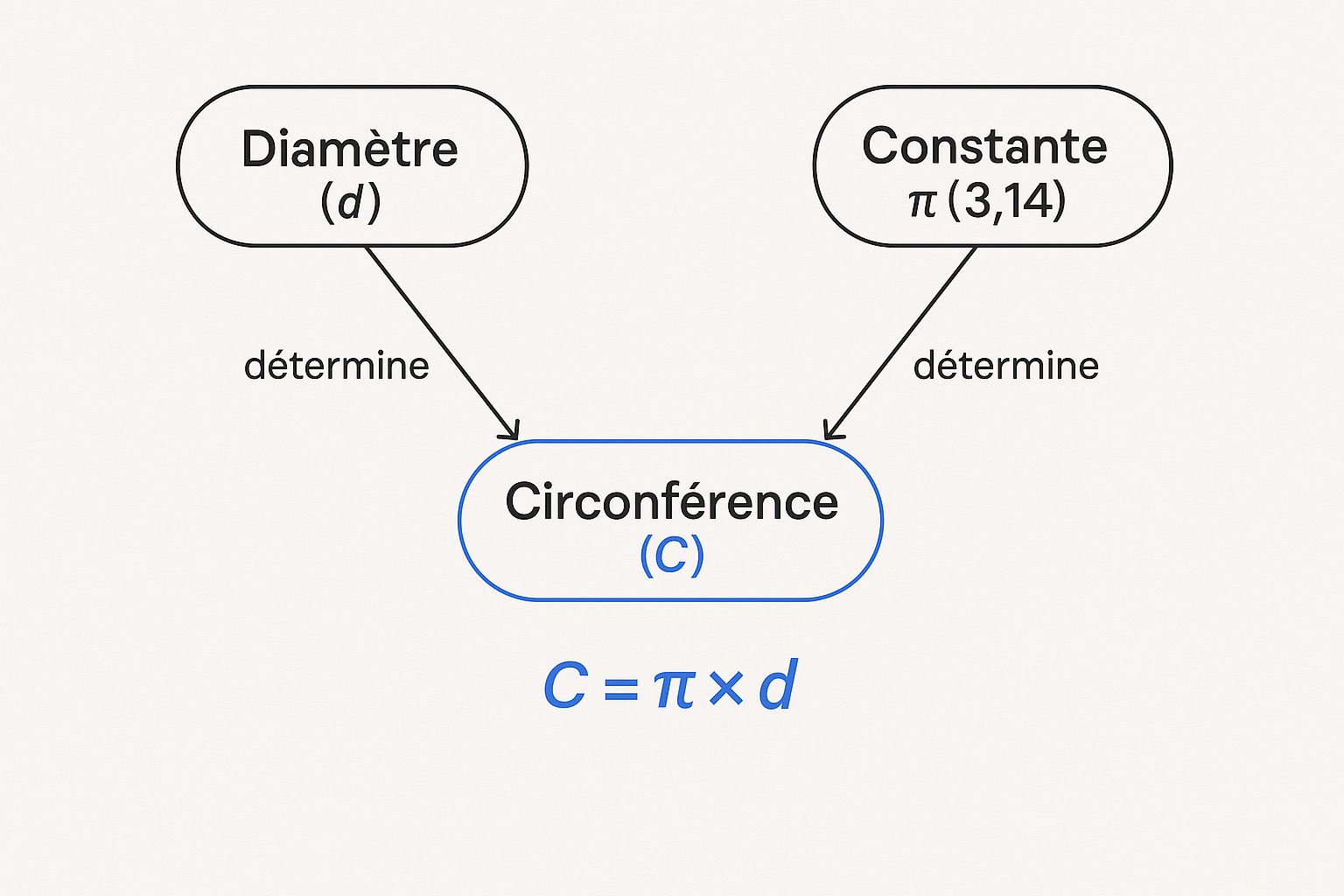
Elle nous montre de manière très claire qu'il suffit de multiplier la longueur du diamètre par la valeur de Pi pour obtenir la circonférence. C'est aussi simple que ça
Le rôle essentiel de la constante Pi
Pour bien saisir comment on calcule la circonférence d'un cercle, il faut d'abord faire connaissance avec son ingrédient secret : le fameux nombre Pi (π). Loin d'être un simple chiffre, Pi est une constante mathématique qui révèle une vérité fondamentale sur absolument tous les cercles.
En fait, Pi représente le rapport qui existe entre la circonférence d’un cercle et son diamètre. Peu importe la taille du cercle, que ce soit une petite pièce de monnaie ou l'équateur de la Terre, si vous divisez sa circonférence par son diamètre, le résultat sera toujours Pi.
C’est cette constance qui rend la formule de la circonférence si fiable. C'est la clé qui relie directement le diamètre d'un cercle à la mesure de son contour.
La fascinante histoire de Pi
La quête pour définir Pi ne date pas d'hier, elle remonte à des milliers d'années. Les mathématiciens de l'Antiquité, comme le génie grec Archimède, étaient déjà captivés par ce mystère. Il a d'ailleurs été l'un des premiers à obtenir une estimation très précise de π en l'encadrant entre des polygones. Vous pouvez explorer les détails de cette approche grâce aux travaux d'Archimède sur le cercle via Accromath.
Cette quête de précision n'est pas qu'un détail pour les passionnés d'histoire; elle a des conséquences bien réelles. La valeur de Pi que vous utilisez change directement la justesse de votre résultat.
Pour la plupart des exercices scolaires, utiliser 3,14 est amplement suffisant. Par contre, en ingénierie, en physique ou en astronomie, chaque décimale a son importance. Une calculatrice scientifique, par exemple, utilise une version bien plus longue de Pi pour garantir des calculs précis.
Pour vous donner une idée, une minuscule différence dans la valeur de Pi pourrait causer une erreur de plusieurs kilomètres dans le calcul d'une orbite de planète. C'est pourquoi bien comprendre Pi est crucial, non seulement pour la géométrie de base, mais aussi pour des calculs plus avancés comme le calcul du volume d'un cylindre, qui dépend directement des propriétés du cercle.
Applications du calcul dans notre quotidien
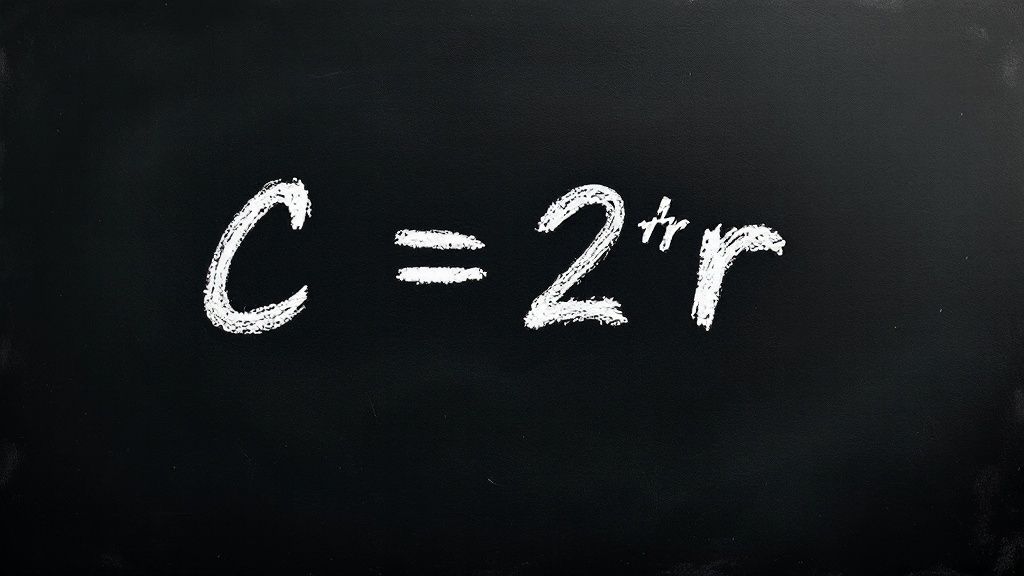
Le calcul de la circonférence d'un cercle est loin d'être un simple exercice abstrait réservé aux salles de classe. En réalité, cette formule est un outil étonnamment pratique, utilisé chaque jour dans une foule de domaines bien concrets, souvent sans même qu'on s'en aperçoive.
Pensez un instant aux ingénieurs et aux designers. Que ce soit pour concevoir une roue de vélo, la lame d’une scie circulaire ou les minuscules engrenages d’une montre, la précision est reine. Ils doivent calculer la circonférence pour garantir que chaque pièce s’ajuste et fonctionne en parfaite harmonie avec les autres.
Cette même logique s'applique à bien plus grande échelle. Dans les grands projets d'ingénierie mécanique, la modélisation exacte des pièces circulaires est fondamentale. Pour les fabricants de pièces d'avion, par exemple, la formule C = 2πr est une étape incontournable pour définir les tolérances de roues, de joints ou de moteurs.
De l'architecture au sport
L'utilité de la circonférence ne s'arrête pas aux portes de l'industrie. En urbanisme, les architectes s'en servent pour dessiner des places publiques, des ronds-points ou des fontaines aux courbes harmonieuses. Un calcul précis assure que les bordures, les sentiers et les éléments décoratifs s'intègrent parfaitement à l'espace.
Imaginez un athlète sur une piste de course. Pour savoir quelle distance il parcourt en un tour, il doit connaître la circonférence de la piste. Un couloir intérieur n’aura pas la même circonférence que le couloir extérieur, et c’est précisément ce qui explique les départs décalés lors des compétitions!
Même en cuisine, la circonférence a son mot à dire! Déterminer la bonne quantité de pâte pour garnir le pourtour d'un moule à tarte repose sur ce simple calcul. C’est la preuve que cette formule est un savoir-faire aussi pratique que la conversion de mesures, une compétence essentielle au quotidien.
Voici quelques exemples pour illustrer tout ça :
- Artisanat : Un menuisier qui fabrique une table ronde doit calculer sa circonférence pour y ajouter une bordure décorative sur mesure.
- Jardinage : Pour savoir quelle longueur de clôture acheter afin d'entourer un parterre de fleurs circulaire.
- Automobile : Les constructeurs calculent la circonférence des pneus pour calibrer avec précision les compteurs de vitesse et les odomètres de nos voitures.
Mettre la formule en pratique avec des exercices
Après la théorie, place à la pratique! La meilleure façon de vraiment maîtriser une nouvelle notion, c'est de l'appliquer concrètement. C'est pourquoi nous vous avons préparé quelques exercices pour bien assimiler le calcul de la circonférence d'un cercle.
Ces problèmes sont conçus pour vous mettre en confiance et vous aider à jongler avec les formules. On va commencer doucement avant de corser un peu les choses. L'objectif n'est pas juste de trouver la bonne réponse, mais de bien comprendre la logique derrière chaque étape.
Exercice 1 : Calculer la circonférence avec le rayon
Le premier défi est un grand classique. Imaginez que vous avez une roue de vélo dont le rayon mesure 35 cm. Quelle est sa circonférence?
- Formule à utiliser :
C = 2πr - Données : r = 35 cm et π ≈ 3,14
- Calcul : C = 2 x 3,14 x 35
- Solution : C = 219,8 cm
La circonférence de la roue est donc d'environ 219,8 cm. Chaque tour complet de cette roue vous fera avancer de presque 2,2 mètres!
Ce type de calcul, même s'il paraît simple, est la pierre angulaire pour résoudre des problèmes bien plus complexes. Il s’apparente aux principes fondamentaux de la géométrie, un peu comme savoir comment calculer l'aire d'un triangle est essentiel pour aborder des formes plus élaborées.
Exercice 2 : Trouver le diamètre à partir de la circonférence
Maintenant, inversons un peu le problème. Vous avez un cerceau dont la circonférence totale est de 157 cm. Comment faire pour trouver son diamètre?
Ici, on part de la formule C = πd et on l'isole pour trouver d. Cela nous donne d = C / π.
- Formule à utiliser :
d = C / π - Données : C = 157 cm et π ≈ 3,14
- Calcul : d = 157 / 3,14
- Solution : d = 50 cm
Le diamètre du cerceau est donc de 50 cm. En maîtrisant ces deux types de problèmes, vous êtes prêt à appliquer la formule de la circonférence dans n'importe quelle situation pratique.
Explorer au-delà de la circonférence

Savoir calculer la circonférence d'un cercle est une compétence essentielle, mais ce n'est vraiment que le début de l'aventure en géométrie. Cette connaissance de base est en fait un tremplin vers des concepts beaucoup plus larges et tout aussi intéressants, qu'on retrouve partout dans le monde qui nous entoure.
La géométrie du cercle ne se limite pas à son périmètre. Elle nous donne les outils pour explorer et mesurer des portions de cette courbe, ce qui ouvre la porte à des calculs plus pointus et très utiles.
Calculer la longueur d'un arc de cercle
Imaginez une pointe de tarte. L'arc de cercle, c'est un peu comme la croûte de cette pointe : c'est une section du contour du cercle. Savoir calculer sa longueur est crucial dans bien des domaines techniques.
Par exemple, les ingénieurs civils s'en servent pour dessiner les courbes des routes et des chemins de fer avec précision. Chaque virage est en fait un arc de cercle, et sa longueur doit être calculée à la perfection pour garantir la sécurité et le confort des usagers.
On peut aussi penser aux orbites des planètes. Même si elles sont souvent de forme elliptique, la compréhension des arcs de cercle est fondamentale pour modéliser leurs trajectoires dans l'espace.
Des cercles aux formes plus complexes
Le cercle est la courbe la plus simple qui soit, mais les principes qui le régissent s'appliquent aussi à d'autres figures. Prenez l'ellipse, sa cousine un peu étirée. Calculer son périmètre est beaucoup plus compliqué et il n'existe pas de formule aussi simple que pour le cercle.
Cela nous montre à quel point la circonférence d'un cercle est un point de départ à la fois élégant et puissant. C'est un peu comme l'aire du cercle, qui est essentielle pour comprendre des objets en trois dimensions. C'est d'ailleurs ce qu'illustre la formule de l'aire d'un cylindre. La circonférence, elle, est la clé pour comprendre le périmètre de n'importe quelle forme courbe.
Vous avez des questions sur la circonférence? On y répond!
Pour être certain que tout est bien clair, passons en revue quelques questions qui reviennent souvent sur la circonférence d'un cercle. Ces réponses rapides et directes vous aideront à solidifier vos acquis.
Peut-on calculer la circonférence sans connaître Pi?
Non, c'est tout simplement impossible. La constante Pi (π) est l'ingrédient secret qui lie le diamètre d'un cercle à son contour. Elle incarne ce rapport universel, ce qui la rend absolument indispensable à la formule. Sans Pi, il n'y aurait aucune connexion proportionnelle entre ces deux mesures.
Quelle est la différence entre circonférence et périmètre?
En fait, ces deux mots désignent la même chose : la mesure du contour d'une forme géométrique. La seule différence, c'est une question d'habitude. On réserve le mot « circonférence » spécifiquement pour les cercles, alors que « périmètre » s'utilise plutôt pour les polygones, comme un carré ou un triangle.
En bref, la circonférence, c'est juste le nom qu'on donne au périmètre d'un cercle.
Si certains de ces concepts vous semblent encore un peu abstraits, un coup de pouce personnalisé pourrait tout changer. Le tutorat en maths est une excellente façon de bâtir votre confiance et de bien maîtriser les notions de géométrie.
Pour un accompagnement scolaire adapté à chaque élève, faites confiance à Centrétudes. Découvrez nos services de tutorat personnalisé sur https://centretudes.ca.


