Maîtriser la loi de sinus facilement

En trigonométrie, il existe une formule particulièrement utile qui relie les longueurs des côtés d'un triangle aux sinus de leurs angles opposés : c'est la loi des sinus. C'est un outil indispensable pour trouver une mesure manquante, que ce soit un côté ou un angle, dans n'importe quel triangle, et pas seulement dans les triangles rectangles.

Qu'est-ce que la loi des sinus?

Imaginez un arpenteur qui doit mesurer la largeur d’une rivière infranchissable. Comment s'y prend-il? La réponse se trouve dans la trigonométrie, et plus précisément dans la loi des sinus. C’est un outil puissant qui permet de travailler avec des triangles qui n’ont pas d’angle droit, ce qui le rend beaucoup plus polyvalent que le théorème de Pythagore ou les rapports SOH-CAH-TOA.

Loin d'être une formule abstraite sortie de nulle part, la loi des sinus est une véritable clé pour comprendre les relations entre les angles et les côtés d'un triangle. Son principe est étonnamment simple : pour n'importe quel triangle, le rapport entre la longueur d'un côté et le sinus de l'angle qui lui fait face est toujours le même pour les trois paires côté-angle. C'est cet équilibre parfait qui nous permet de trouver les pièces manquantes du puzzle.

Quand utiliser cet outil

Le moment idéal pour sortir la loi des sinus de votre coffre à outils, c'est lorsque vous connaissez une paire "côté et son angle opposé". Si vous avez cette paire complète, plus une autre information (un autre angle ou un autre côté), alors vous pouvez calculer l'élément qui lui manque.

Voici les scénarios où la loi des sinus est votre meilleure alliée :

AAC (Angle-Angle-Côté) : Vous connaissez deux angles et un côté qui n'est pas entre ces deux angles.
ACA (Angle-Côté-Angle) : Vous connaissez deux angles et le côté qui se trouve juste entre eux.
CCA (Côté-Côté-Angle) : Vous connaissez deux côtés et un angle qui n'est pas entre ces deux côtés.

Pour vous aider à visualiser rapidement quand l'utiliser, voici un petit tableau récapitulatif.

Quand utiliser la loi des sinus

Ce tableau vous aide à identifier rapidement les situations où la loi des sinus est l'outil idéal pour résoudre votre triangle.

Scénario du problème	Ce que vous connaissez	Ce que vous pouvez trouver
Angle-Angle-Côté (AAC)	Deux angles et un côté non adjacent.	Le côté opposé à l'un des angles connus.
Angle-Côté-Angle (ACA)	Deux angles et le côté situé entre eux.	Les deux autres côtés (après avoir trouvé le 3e angle).
Côté-Côté-Angle (CCA)	Deux côtés et un angle opposé à l'un d'eux.	L'angle opposé à l'autre côté connu.

Ce tableau montre bien comment, à partir de certaines informations, on peut déduire le reste.

La loi des sinus transforme ce qui peut sembler être un problème de géométrie insoluble en une simple série de calculs. C'est souvent le point de départ pour analyser et résoudre la plupart des triangles non rectangles.

Fait intéressant, les origines de cette loi remontent aux travaux d'Abu Nasr Mansur au XIe siècle, avant d'être officiellement formulée par Nasir al-Din al-Tusi au XIIIe siècle. Pour ceux qui aiment l'histoire des maths, vous pouvez consulter cette page sur la loi des sinus pour en apprendre davantage.

Maîtriser cette loi est aussi un tremplin pour comprendre d'autres concepts de géométrie, comme les relations entre les droites parallèles. Si ce sujet vous intéresse, jetez un œil à notre guide sur les propriétés d'un angle alterne-interne.

Comprendre la formule et son origine

Pour vraiment maîtriser la loi des sinus, il ne suffit pas de mémoriser une formule. Le secret, c'est de comprendre sa logique, sa mécanique interne. C’est ce qui transforme une règle mathématique un peu abstraite en un outil puissant que vous pouvez utiliser avec confiance.

La formule en elle-même est plutôt élégante :

a / sin(α) = b / sin(β) = c / sin(γ)

Décortiquons ça ensemble. Dans n'importe quel triangle, « a », « b » et « c » sont les longueurs des côtés. De leur côté, les lettres grecques alpha (α), bêta (β) et gamma (γ) représentent les angles qui leur font directement face. La formule nous dit simplement que pour un triangle donné, le rapport entre la longueur d'un côté et le sinus de son angle opposé est toujours le même.

Cette image illustre parfaitement cette relation entre chaque côté et son angle opposé.

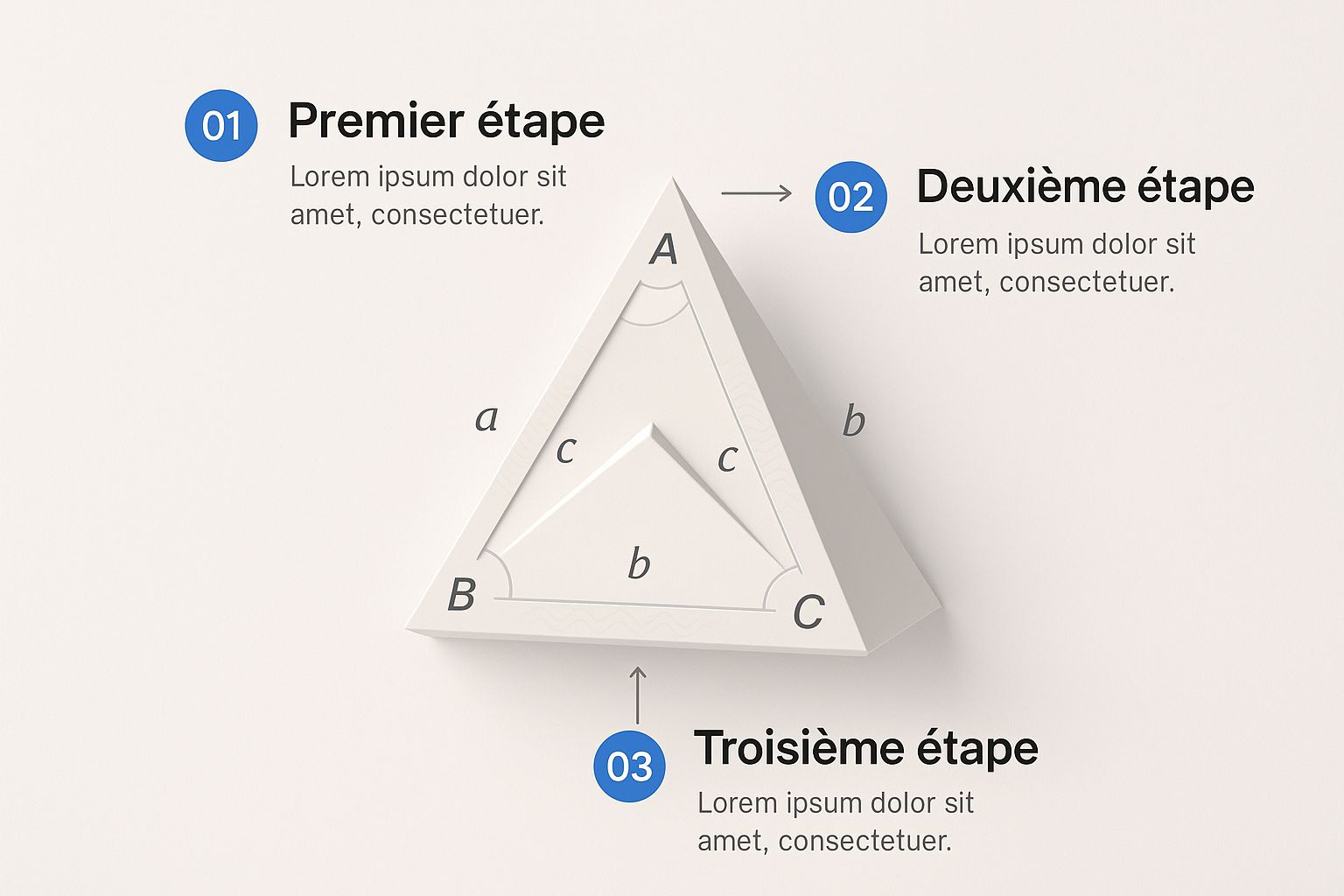
En regardant bien le triangle, on voit tout de suite que le côté « a » fait face à l’angle α, le côté « b » fait face à l’angle β, et ainsi de suite. C'est le fondement même de la loi des sinus.

La preuve par la hauteur

Mais d’où sort cette belle relation? Elle n'est pas tombée du ciel. On peut la prouver très simplement avec une petite astuce : tracer la hauteur du triangle.

Imaginez qu'on dessine une ligne droite partant d’un sommet et qui arrive perpendiculairement sur le côté opposé. Cette ligne, c'est la hauteur (on va l'appeler h). En faisant ça, on vient de diviser notre triangle quelconque en deux triangles rectangles. Et là, tout s'éclaire, car on sait très bien travailler avec les triangles rectangles grâce à nos bons vieux rapports trigonométriques (SOH-CAH-TOA).

Dans le premier triangle rectangle, le sinus de l'angle α est égal au côté opposé (h) divisé par l'hypoténuse (le côté b). On a donc : sin(α) = h / b.
Dans le deuxième triangle rectangle, le sinus de l'angle β est égal au côté opposé (h) divisé par l'hypoténuse (le côté a). On a donc : sin(β) = h / a.

On se retrouve avec deux équations qui ont un point en commun : notre fameuse hauteur h.

Assembler les morceaux du casse-tête

Maintenant, il suffit d'isoler h dans chacune des équations pour voir le lien apparaître sous nos yeux.

De la première équation, on tire : h = b * sin(α)
De la deuxième, on obtient : h = a * sin(β)

Puisque h est évidemment égal à lui-même, on peut poser que b * sin(α) = a * sin(β). Il ne reste plus qu'à réarranger un peu les termes pour regrouper les côtés avec leurs angles. On arrive à :

a / sin(α) = b / sin(β)

En refaisant exactement le même raisonnement avec une autre hauteur du triangle, on prouverait que ce rapport est aussi égal à c / sin(γ). Et voilà! La loi des sinus prend tout son sens. Ce n'est plus une règle arbitraire, mais une conséquence logique de la géométrie la plus fondamentale.

D'ailleurs, cette approche est directement liée à d'autres concepts. La hauteur, par exemple, est aussi un élément central pour calculer l'aire d'un triangle. Ça montre bien comment tout est connecté en mathématiques. Une fois qu'on a compris d'où vient la loi des sinus, l'appliquer devient beaucoup plus intuitif.

Appliquer la loi de sinus pas à pas

Maintenant que la théorie est derrière nous, mettons les mains à la pâte. La loi des sinus est un outil puissant, et pour bien s'en servir, il faut savoir qu'on l'utilise principalement dans deux situations : le cas Angle-Angle-Côté (AAC) et le cas un peu plus spécial, Côté-Côté-Angle (CCA).

Une fois que vous aurez compris comment aborder ces deux scénarios, vous serez capable de résoudre la grande majorité des problèmes impliquant des triangles quelconques. Voyons ça étape par étape.

Le cas simple : Angle-Angle-Côté (AAC)

Commençons par le plus facile. Ici, on vous donne deux angles et un côté. Le gros du travail est déjà fait. Puisque la somme des angles dans un triangle fait toujours 180°, trouver le troisième angle est un jeu d'enfant.

Ensuite, un petit coup de loi des sinus, et hop, vous trouvez les côtés qui vous manquent.

Imaginons un triangle avec les informations suivantes :

Angle α = 45°
Angle β = 60°
Côté a = 10 cm (le côté opposé à l'angle α)

1. On trouve l'angle manquant (γ)
C'est simple : γ = 180° – 45° – 60° = 75°.

2. On applique la loi des sinus
Disons qu'on veut trouver la longueur du côté b. On prend la partie de la formule qui nous intéresse :
a / sin(α) = b / sin(β)
10 / sin(45°) = b / sin(60°)

3. On isole et on calcule
Un peu d'algèbre de base pour trouver b :
b = 10 * sin(60°) / sin(45°)
b ≈ 10 * 0.866 / 0.707
b ≈ 12,25 cm

Et voilà ! Le côté b est trouvé. Ce raisonnement fonctionne à tous les coups pour les cas AAC.

Le cas ambigu : Côté-Côté-Angle (CCA)

Bon, ici, ça se complique un peu. On l'appelle le cas « ambigu » pour une bonne raison : avec les mêmes informations de départ, on peut parfois obtenir une seule solution, deux solutions, ou même aucune solution ! C'est le scénario qui demande le plus d'attention.

Mais d'où vient cette ambiguïté ? Quand on utilise la loi des sinus pour trouver un angle, on se retrouve avec une équation du type sin(θ) = une valeur. Le piège, c'est qu'entre 0° et 180°, il y a toujours deux angles qui ont le même sinus : un angle aigu (θ) et son cousin obtus (180° – θ).

La clé pour s'en sortir est de toujours se demander si la deuxième solution, l'angle obtus, est logiquement possible. Si cet angle, additionné à celui que vous connaissez déjà, donne un total de plus de 180°, alors il est impossible. Un triangle ne peut pas avoir des angles qui totalisent plus de 180°.

Prenons un exemple pour que ce soit plus clair :

Côté a = 6 cm
Côté b = 8 cm
Angle α = 30°

1. On choisit la bonne formule
On cherche l'angle β, donc on pose :
a / sin(α) = b / sin(β)
6 / sin(30°) = 8 / sin(β)

2. On isole l'inconnu
On manipule l'équation pour isoler sin(β) :
sin(β) = 8 * sin(30°) / 6
sin(β) = 8 * 0,5 / 6
sin(β) ≈ 0,667

3. On vérifie les solutions possibles
Avec une calculatrice, on trouve la première solution, qui est un angle aigu :
β₁ ≈ arcsin(0,667) ≈ 41,8°

Maintenant, le réflexe à avoir : tester la deuxième possibilité, l'angle obtus :
β₂ = 180° – 41,8° = 138,2°

Est-ce que cette deuxième solution est valide ? Pour le savoir, on l'ajoute à l'angle qu'on connaissait au départ :
α + β₂ = 30° + 138,2° = 168,2°.

Puisque 168,2° est inférieur à 180°, il reste de la place pour un troisième angle. La solution est donc parfaitement valide ! Dans cette situation précise, il existe donc deux triangles différents qui respectent les données de départ.

Cette gymnastique intellectuelle consistant à valider des solutions est courante en géométrie. Elle rappelle un peu les étapes nécessaires quand on cherche à comment calculer la pente, où chaque étape doit être logiquement justifiée.

La loi des sinus dans le monde réel

On pourrait croire que la trigonométrie est un concept purement abstrait, confiné aux manuels scolaires. Pourtant, la loi des sinus est tout sauf un simple exercice théorique. C’est un outil incroyablement concret qui a permis de résoudre des problèmes majeurs et de façonner notre compréhension du monde, bien au-delà des salles de classe.

De l'infiniment grand jusqu'à la construction de nos infrastructures, ses applications sont partout. On peut la voir comme le couteau suisse du géomètre, de l’ingénieur et même de l’astronome.

Mesurer l’univers depuis la Terre

Comment fait-on pour connaître la distance qui nous sépare d'une étoile lointaine? C'est une excellente question! Les astronomes utilisent une méthode ingénieuse appelée la triangulation stellaire, et la loi des sinus est au cœur de ce processus. L'idée est de mesurer la position d'une étoile à six mois d'intervalle, lorsque la Terre se trouve à des points opposés de son orbite. Cette manoeuvre crée un immense triangle dans l'espace.

Concrètement, les astronomes connaissent :

La distance entre les deux points d'observation (qui correspond au diamètre de l'orbite terrestre).
Les deux angles sous lesquels ils observent l'étoile depuis ces deux points.

Avec ces informations en main (un cas ACA, Angle-Côté-Angle), la loi des sinus leur permet de calculer la longueur des deux autres côtés du triangle, qui représentent justement la distance jusqu'à l'étoile. C'est en grande partie comme ça qu'on a réussi à cartographier notre galaxie.

Bâtir le monde avec précision

En ingénierie et en architecture, la précision n'est pas une option, c'est une nécessité. Pensez à la conception d'un pont suspendu ou d'un dôme géodésique. Ces structures impressionnantes sont en fait un assemblage complexe de triangles qui doivent répartir les forces de manière optimale pour garantir la stabilité de l'ensemble.

La loi des sinus permet aux ingénieurs de calculer avec une exactitude redoutable les longueurs et les angles requis pour chaque poutre et chaque joint, même pour des formes qui semblent complètement irrégulières. Cela assure que chaque composant s'emboîte parfaitement, garantissant ainsi la sécurité et la durabilité de la structure.

La loi des sinus est aussi appliquée en géométrie pratique pour déterminer des aires et distances dans des projets d'arpentage. La formule d’aire A = (1/2)ab sin(C), qui en dérive, facilite le calcul sans avoir besoin de mesurer la hauteur. Cette méthode a permis de réduire de 17 % le temps nécessaire au relevé topographique par rapport aux approches traditionnelles dans certains projets. Découvrez-en plus sur ces applications pratiques de la trigonométrie.

Naviguer en toute sécurité

Bien avant l'arrivée du GPS, comment les marins faisaient-ils pour savoir où ils se trouvaient en pleine mer? Ils se fiaient à la triangulation et, vous l'aurez deviné, à la loi des sinus. En repérant deux points de repère connus sur la côte (un phare et une montagne, par exemple) et en mesurant les angles entre leur bateau et ces points, ils pouvaient former un triangle.

En connaissant la distance entre les deux repères (un côté) et les deux angles observés, ils utilisaient la loi des sinus pour calculer leur distance exacte par rapport à la côte. Bien que cette technique soit plus rare aujourd'hui, elle reste un principe fondamental de la navigation. Ces applications démontrent bien l'importance de maîtriser les calculs et les unités, un sujet que nous abordons dans notre guide sur la conversion de mesure.

Mettez-vous à l'épreuve : exercices corrigés

La meilleure façon de s'approprier une nouvelle notion, c'est de la mettre en pratique. Maintenant que la théorie et les applications de la loi des sinus sont plus claires, il est temps de passer à l'action. Les problèmes qui suivent ont été pensés pour vous faire progresser en douceur, en commençant par un calcul simple pour aller vers un cas un peu plus complexe.

Chaque exercice vient avec sa correction détaillée, étape par étape. L'idée n'est pas juste de vous donner la bonne réponse, mais de vous montrer le cheminement pour y arriver par vous-même, avec assurance.

Problème 1 : Trouver la longueur d'un côté

Commençons par un exercice classique pour se mettre en jambe. C'est le scénario typique où l'on connaît deux angles et un côté, et où l'on doit trouver la longueur d'un autre côté.

Les données du problème
Imaginez un triangle ABC avec les informations suivantes :

L'angle A = 50°
L'angle B = 70°
Le côté b (celui qui fait face à l'angle B) mesure 15 cm.
Votre mission : trouver la longueur du côté a.

Correction détaillée

Repérer la paire connue : On a tout ce qu'il faut avec l'angle B (70°) et son côté opposé, b (15 cm). C'est notre point de départ, notre ancre.
Mettre la formule en place : On utilise la loi des sinus en se concentrant sur les deux paires qui nous intéressent, a/sin(A) et b/sin(B) :
a / sin(A) = b / sin(B)
Remplacer par les chiffres :
a / sin(50°) = 15 / sin(70°)
Isoler et calculer 'a' : Un peu d'algèbre simple. Pour isoler 'a', il suffit de multiplier chaque côté par sin(50°) :
a = (15 / sin(70°)) * sin(50°)
a ≈ (15 / 0,940) * 0,766
a ≈ 15,96 * 0,766
a ≈ 12,23 cm

Voilà ! La longueur du côté a est d'environ 12,23 cm.

Le réflexe à avoir est toujours le même : commencer par identifier la paire angle-côté que vous connaissez. C'est la clé qui vous permettra de déverrouiller tout le reste du triangle avec la loi des sinus.

Problème 2 : Trouver la mesure d’un angle

On monte un peu le niveau de difficulté. Cette fois, c'est un angle que l'on cherche. C'est ici qu'il faut faire attention au fameux « cas ambigu », où plus d'une solution pourrait exister.

Les données du problème
Soit un triangle XYZ dont vous connaissez :

Le côté x = 8 cm
Le côté y = 6 cm
L'angle Y (opposé au côté y) = 35°
Votre mission : trouver la mesure de l'angle X.

Correction détaillée

Poser l'équation : On applique la loi des sinus avec les paires x/sin(X) et y/sin(Y), comme tout à l'heure :
x / sin(X) = y / sin(Y)
Substituer les valeurs connues :
8 / sin(X) = 6 / sin(35°)
Isoler sin(X) : On réarrange un peu l'équation pour trouver la valeur du sinus de l'angle X :
sin(X) = (8 * sin(35°)) / 6
sin(X) ≈ (8 * 0,574) / 6
sin(X) ≈ 4,592 / 6
sin(X) ≈ 0,765
Trouver l'angle et vérifier le cas ambigu :
- Première solution possible : On utilise la fonction arcsin (ou sin⁻¹) pour trouver l'angle aigu :
  X₁ = arcsin(0,765) ≈ 49,9°
- Vérifier s'il y a une deuxième solution : L'autre angle qui pourrait avoir le même sinus est 180° – 49,9° = 130,1°. Pour savoir si cette solution est valide, on l'additionne à l'angle qu'on connaît déjà : 130,1° + 35° = 165,1°. Puisque ce total est inférieur à 180°, cette solution est parfaitement possible ! Il y a donc deux triangles qui peuvent exister avec ces mesures.

C'est en pratiquant régulièrement qu'on devient à l'aise avec ces nuances. Si vous sentez que vous bloquez sur certains points, un accompagnement personnalisé peut vraiment faire la différence. Découvrez comment le tutorat en maths peut vous aider à solidifier vos bases.

Quelques questions fréquentes sur la loi des sinus

Même après avoir bien compris la théorie et fait quelques exercices, il reste souvent des petites zones d'ombre. C'est tout à fait normal. Cette section est là pour répondre aux questions les plus courantes sur la loi des sinus et vous donner la confiance nécessaire pour l'utiliser sans hésiter.

Allons droit au but et attaquons les interrogations qui reviennent le plus souvent.

Loi des sinus ou loi des cosinus?

C'est LA grande question! Comment savoir laquelle choisir? Tout dépend des informations que vous avez sous la main. C'est un peu comme choisir le bon outil dans son coffre : on ne prend pas un marteau pour visser une vis.

Pensez « loi des sinus » dès que vous connaissez un duo angle-côté opposé. Si vous avez un angle et la mesure du côté qui lui fait face, en plus d'une autre information (un autre angle ou un autre côté), c'est votre meilleure alliée. Elle est parfaite pour les situations AAC, ACA et CCA.
Tournez-vous vers la loi des cosinus quand vous connaissez soit les trois côtés du triangle (CCC), soit deux côtés et l'angle coincé entre les deux (CAC). Dans ces cas-là, il vous manque un duo angle-côté complet, ce qui empêche d'utiliser la loi des sinus au départ.

Un bon truc pour s'en souvenir : la loi des sinus connecte les opposés (angle et côté qui se font face), alors que la loi des cosinus est la spécialiste des voisins (deux côtés qui entourent un angle).

Est-ce qu'on peut l'utiliser pour un triangle rectangle?

La réponse courte : oui, absolument! La loi des sinus est universelle et fonctionne pour tous les triangles, sans exception, y compris les triangles rectangles. Si vous l'utilisez, vos calculs seront justes.

Par contre, c'est un peu comme sortir l'artillerie lourde pour écraser une mouche. Pour un triangle rectangle, les bons vieux rapports trigonométriques (SOH-CAH-TOA) sont tellement plus simples et rapides. Comme vous connaissez déjà un angle de 90°, les calculs avec le sinus, le cosinus ou la tangente sont beaucoup plus directs. Bref, c'est possible, mais ce n'est pas la méthode la plus efficace.

Comment ne pas se tromper avec le fameux cas ambigu?

Ah, le cas CCA (Côté-Côté-Angle)! Il peut faire un peu peur avec la possibilité d'avoir deux solutions. Mais pas de panique, le secret, c'est d'être méthodique.

Quand vous utilisez la loi des sinus pour trouver un angle, votre calculatrice vous donnera toujours l'angle aigu (celui entre 0° et 90°). Voici la marche à suivre pour ne jamais vous tromper :

Trouvez la première solution (l'angle aigu que votre calculatrice vous donne).
Cherchez la deuxième solution possible en faisant simplement 180° – (le premier angle trouvé).
Vérifiez si elle est logique : additionnez ce deuxième angle avec celui que vous connaissiez au départ. Si la somme est moins de 180°, alors cette solution est valide, et il existe deux triangles possibles. Si ça dépasse 180°, c'est impossible, et vous pouvez l'ignorer.

En suivant ces trois étapes, vous saurez toujours avec certitude si vous avez une, deux, ou même aucune solution.

Se frayer un chemin dans le monde de la trigonométrie peut parfois sembler complexe, mais avec le bon accompagnement, chaque élève peut y arriver. Chez Centretudes, nos tuteurs spécialisés offrent un soutien personnalisé pour transformer les doutes en confiance. Découvrez comment nous pouvons aider votre enfant à maîtriser les mathématiques en visitant notre site : https://centretudes.ca.