La formule du volume est un outil mathématique essentiel pour mesurer l'espace qu'un objet occupe en trois dimensions. C'est ce qui nous permet de savoir combien de jus contient un carton, quelle quantité d'eau il faut pour remplir une piscine ou même combien d'air se trouve dans un ballon.
Comprendre le volume et son importance au quotidien

Avez-vous déjà suivi une recette de cuisine à la lettre ou tenté de faire entrer tous vos vêtements dans une valise? Si oui, vous avez déjà une excellente idée de ce qu'est le volume. C'est tout simplement la mesure de l'espace qu'un objet peut contenir ou occuper.
Pensez à un château de sable sur la plage. L'aire, c'est la surface que votre château couvre au sol. Le volume, quant à lui, c'est la quantité totale de sable dont vous avez besoin pour le construire en hauteur. C'est une notion bien plus concrète qu'il n'y paraît et qui va bien au-delà des salles de classe.
Le volume dans le monde réel
Savoir utiliser la formule du volume est une compétence très pratique. Elle nous aide à répondre à des questions que l'on se pose tous les jours.
- En cuisine : Mesurer des litres de lait ou des millilitres d'huile, c'est se servir du volume pour que la recette soit une réussite.
- Au jardin : Calculer la quantité de terre nécessaire pour un nouveau pot de fleurs, c'est un calcul de volume tout simple.
- Pour un déménagement : Estimer si tous vos meubles et boîtes tiendront dans le camion, c'est résoudre un grand problème de volume!
Le volume n'est pas qu'un concept abstrait; c'est un langage universel pour décrire l'espace qui nous entoure. Le comprendre, c'est mieux interagir avec le monde physique, de la plus petite tasse de café à la plus grande piscine.
Ce guide est là pour démystifier le calcul du volume. Nous allons décortiquer les formules pour les formes les plus courantes — cubes, cylindres, sphères — à l'aide d'exemples faciles à suivre et d'explications limpides. Notre but est de rendre cette notion, parfois intimidante, accessible et utile pour tout le monde.
Pour les jeunes qui apprennent ces concepts, les maîtriser peut vraiment faire une différence dans leur parcours scolaire. Un service d'aide aux devoirs et de soutien scolaire peut d'ailleurs offrir l'accompagnement personnalisé nécessaire pour bâtir une confiance solide et durable en mathématiques.
Calculer le volume des prismes et du cylindre

Maintenant qu'on a fait le tour du concept de volume, attaquons-nous à une famille de solides que l'on côtoie tous les jours : les prismes et le cylindre. Pensez à votre boîte de céréales, à un carton de lait ou même à une simple conserve. Tous ces objets du quotidien partagent un secret mathématique aussi puissant que simple.
Leur volume se calcule toujours avec la même idée de base. Que ce soit un petit cube ou un grand cylindre, le principe ne change pas d'un poil.
Formule générale du volume : V = Aire de la base × Hauteur
Cette formule est la clé de tout. Imaginez simplement que vous empilez des tranches identiques de la base, les unes sur les autres, jusqu'à atteindre le sommet. Le volume, c'est tout cet espace que vous venez de remplir.
Décortiquer la formule pour chaque forme
Même si le principe général est le même pour tous, la façon de calculer l'« Aire de la base » va dépendre de la forme du solide. C'est la seule petite subtilité à maîtriser pour devenir un pro du volume.
1. Le pavé droit (ou la boîte rectangulaire)
C'est la forme qu'on voit le plus souvent, comme une boîte à chaussures ou une brique. Sa base est tout simplement un rectangle.
- Aire de la base : Longueur × largeur
- Formule du volume : V = (Longueur × largeur) × Hauteur
Exemple : Une boîte de céréales mesure 20 cm de long, 8 cm de large et 30 cm de haut. Son volume est donc de 20 × 8 × 30 = 4800 cm³.
2. Le cube
Le cube est un cas particulier de prisme où toutes les arêtes sont de la même longueur. Ça rend le calcul encore plus rapide!
- Aire de la base : côté × côté (ou côté²)
- Formule du volume : V = côté × côté × côté (ou côté³)
Exemple : Un dé à jouer de 6 cm de côté a un volume de 6 × 6 × 6 = 216 cm³.
3. Le cylindre
Un cylindre, comme une conserve de soupe, a une base en forme de cercle. C'est ici que notre bon vieil ami Pi (π ≈ 3,14159) fait son entrée.
- Aire de la base : π × rayon² (ou πr²)
- Formule du volume : V = (π × rayon²) × Hauteur
Exemple : Une conserve de 5 cm de rayon et 10 cm de hauteur a un volume de π × 5² × 10 ≈ 3,14159 × 25 × 10 = 785,4 cm³.
Attention aux unités et aux erreurs fréquentes
La justesse de votre résultat dépend beaucoup de la bonne utilisation des unités. Si vos mesures sont en centimètres (cm), alors votre volume sera en centimètres cubes (cm³). Si vous mesurez en mètres (m), le résultat sera en mètres cubes (m³).
Une erreur très commune est de mélanger les unités, par exemple multiplier des centimètres avec des mètres sans les avoir convertis avant. Assurez-vous que toutes vos mesures sont dans la même unité avant de vous lancer dans les calculs pour éviter les mauvaises surprises.
Bien comprendre et appliquer ces formules est une compétence essentielle en mathématiques. Si votre enfant trouve ces notions un peu abstraites, un coup de pouce personnalisé peut faire toute la différence. Découvrez comment le tutorat en mathématiques peut l'aider à bâtir sa confiance et à maîtriser ces concepts fondamentaux.
La formule du volume pour une sphère et ses applications
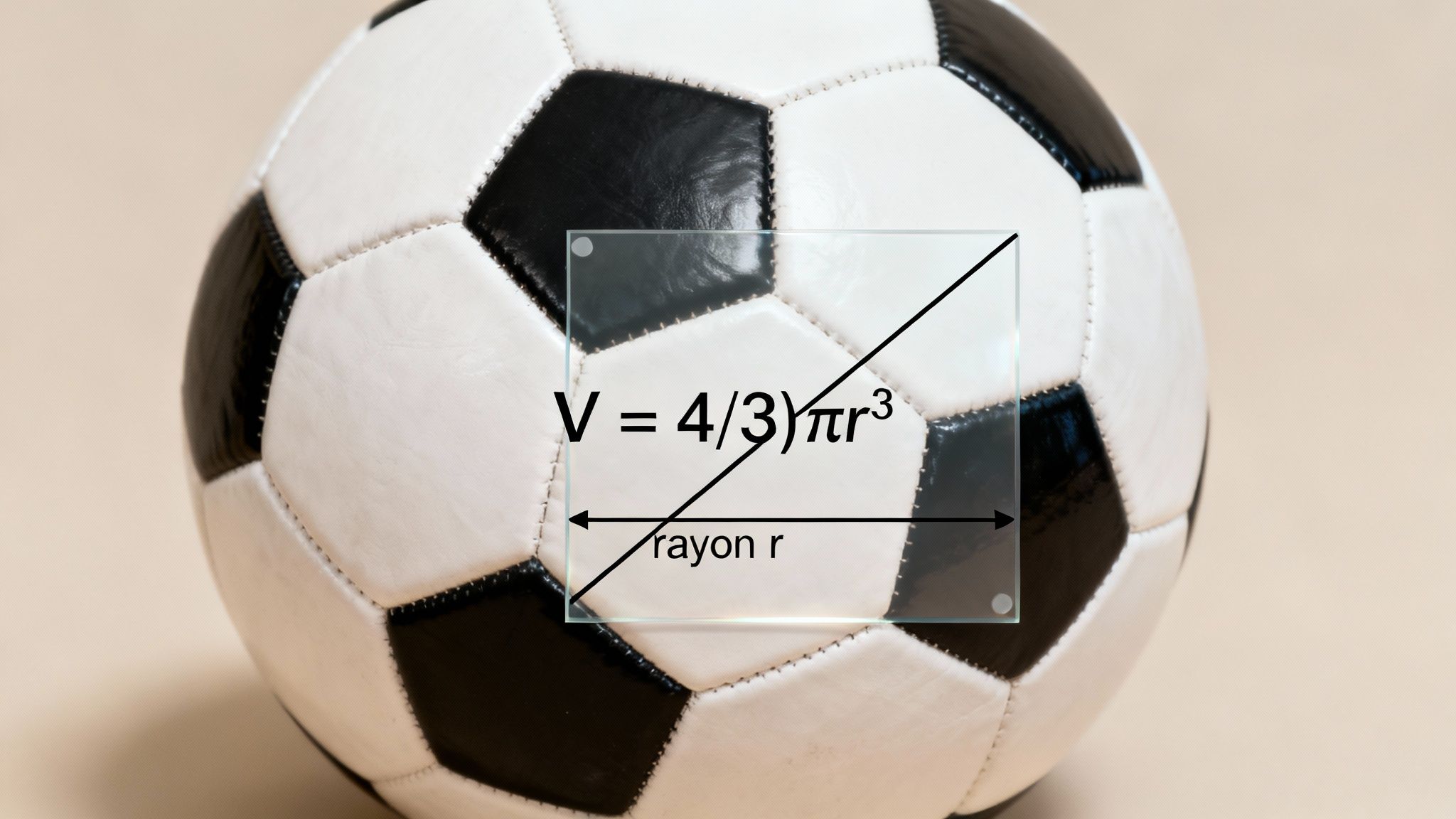
Contrairement aux prismes et aux cylindres, une sphère est une forme parfaitement ronde, sans aucune base plate ni arête. Pensez à une bille, une planète ou un ballon de soccer; voilà des exemples parfaits. On ne peut donc pas calculer leur volume en empilant simplement des surfaces.
Pour percer le secret de l'espace contenu dans une sphère, les mathématiciens ont mis au point une formule aussi spécifique qu'élégante.
Formule du volume de la sphère : V = (4/3)πr³
Elle peut sembler un peu intimidante au premier coup d'œil, mais chaque élément a un rôle bien précis. Une fois qu'on la décompose, elle devient beaucoup plus simple à utiliser.
Comprendre les composantes de la formule
Chaque partie de cette formule est indispensable pour obtenir un résultat juste. Voyons ce que chaque symbole signifie et comment il contribue au calcul final.
- (4/3) : Il s'agit d'une fraction constante. C'est un rapport fixe qui reste le même pour toutes les sphères, peu importe leur taille. Elle représente la relation mathématique unique entre le volume d'une sphère et son rayon.
- π (Pi) : C'est notre fameuse constante, avec une valeur approximative de 3,14159. Elle est essentielle dans tous les calculs qui impliquent des cercles ou des sphères.
- r³ (rayon au cube) : Voici la mesure la plus importante. Le rayon (r) est la distance qui sépare le centre de la sphère de n'importe quel point sur sa surface. On le multiplie par lui-même trois fois (r × r × r) parce que le volume est une mesure en trois dimensions.
Mettre la formule en pratique
Le calcul du volume d'une sphère est une compétence étonnamment utile dans de nombreux domaines, de l'ingénierie à l'agriculture. Au Québec, la formule du volume d'une sphère est cruciale. En 2023, par exemple, la capacité totale des cuves sphériques dans l'industrie pétrochimique atteignait 2,5 millions de m³. De plus, les tests PISA 2022 montrent que 82 % des Québécois de 15 ans résolvent correctement les problèmes de volume sphérique, surpassant ainsi la moyenne de 71 % de l'OCDE. Pour en savoir plus, n'hésitez pas à consulter des calculateurs de volume sphérique en ligne qui détaillent ces applications.
Exemple concret : Calculer le volume d'un ballon de soccer
Imaginons que vous voulez savoir combien d'air peut contenir un ballon de soccer réglementaire.
- Trouver le rayon : Un ballon de taille 5 a un diamètre d'environ 22 cm. Le rayon correspond à la moitié du diamètre, donc r = 11 cm.
- Mettre le rayon au cube : On calcule r³, ce qui donne 11 × 11 × 11 = 1331 cm³.
- Appliquer la formule complète : V = (4/3) × π × 1331.
- Calculer le résultat final : V ≈ (4/3) × 3,14159 × 1331 ≈ 5575 cm³.
Le ballon contient donc environ 5575 centimètres cubes d'air. Cette même logique s'applique pour calculer le volume d'un réservoir de propane ou même la capacité d'un silo sphérique.
La maîtrise de ces concepts géométriques est un atout majeur dans le parcours scolaire. Pour un soutien adapté, le tutorat en sciences peut offrir les outils nécessaires pour transformer des formules abstraites en compétences concrètes et utiles.
Comment maîtriser le volume des pyramides et du cône

Après avoir exploré les formes bien droites comme les prismes et les cylindres, il est temps de se pencher sur les solides qui se terminent en pointe. Les pyramides et les cônes ont une élégance mathématique qui leur est propre, et leur formule de volume cache une astuce plutôt fascinante.
Pour bien comprendre, imaginez un cylindre et un cône qui partagent exactement la même base circulaire et la même hauteur. Si vous remplissiez le cône d'eau pour le verser dans le cylindre, vous remarqueriez qu'il faudrait le faire trois fois pour remplir complètement le cylindre. Cette simple relation d'un tiers est la clé de tout.
Formule générale du volume : V = (1/3) × Aire de la base × Hauteur
Cette formule fonctionne pour tous les solides pointus, que ce soit une grande pyramide égyptienne ou un simple cornet de crème glacée. Le principe reste toujours le même : on calcule d'abord l'aire de sa base, on la multiplie par sa hauteur, puis on divise le résultat par trois.
La formule du volume pour le cône
Le cône est une forme que l'on croise partout, des cônes de signalisation aux volcans. Comme sa base est un cercle, on revient à une formule bien connue pour calculer son aire.
- Aire de la base (un cercle) : π × rayon² (ou πr²)
- Formule du volume du cône : V = (1/3) × (π × rayon²) × Hauteur
Au Québec, cette formule est particulièrement utile. En 2022, elle a été utilisée dans le secteur forestier pour mieux estimer les tas de bois coniques, ce qui a permis une optimisation de 14 % et une réduction des pertes de 8,2 %. Les données scolaires montrent d'ailleurs que 89 % des élèves de 4e secondaire la maîtrisent bien.
Exemple : Calculer le volume d'un cornet de crème glacée
Imaginons un cornet avec un rayon de 3 cm et une hauteur de 10 cm. Quel est son volume?
- Calculer l'aire de la base : π × 3² ≈ 3,14159 × 9 = 28,27 cm²
- Multiplier par la hauteur : 28,27 cm² × 10 cm = 282,7 cm³
- Diviser par trois : 282,7 cm³ ÷ 3 ≈ 94,23 cm³
Le cornet peut donc contenir environ 94,23 cm³ de crème glacée. C'est simple comme bonjour!
La formule pour la pyramide
Pour une pyramide, la logique est exactement la même. La seule chose qui change, c'est la forme de sa base, qui peut être un carré, un rectangle ou même un triangle. Il suffit donc d'adapter le calcul de l'aire de la base.
- Pour une pyramide à base carrée : V = (1/3) × (côté × côté) × Hauteur
- Pour une pyramide à base rectangulaire : V = (1/3) × (Longueur × largeur) × Hauteur
Exemple : La pyramide du Louvre
La célèbre pyramide du Louvre à Paris a une base carrée d'environ 35 mètres de côté et une hauteur de 22 mètres.
- Calculer l'aire de la base : 35 m × 35 m = 1225 m²
- Multiplier par la hauteur : 1225 m² × 22 m = 26 950 m³
- Diviser par trois : 26 950 m³ ÷ 3 ≈ 8983 m³
Son volume intérieur est donc de près de 9000 mètres cubes. Impressionnant, non?
Maîtriser ces concepts peut sembler difficile au début, mais avec un peu de pratique, ça devient vite une seconde nature. Si votre enfant a besoin d'un coup de pouce pour transformer la théorie en compréhension durable, le tutorat en mathématiques est une excellente solution pour renforcer ces compétences.
Éviter les erreurs courantes dans vos calculs de volume
Connaître la bonne formule de volume, c’est un excellent point de départ. Mais c’est en l’appliquant correctement qu’on s’assure d’un résultat juste. Même les élèves les plus attentifs peuvent tomber dans des pièges qui faussent complètement un calcul. Heureusement, ces erreurs sont faciles à éviter une fois qu’on les a repérées.
Considérez cette section comme votre guide de sécurité pour des calculs fiables. En prenant conscience des erreurs les plus fréquentes, vous développerez de bons réflexes pour vérifier votre travail. Résultat? Plus de confiance et de précision dans vos réponses.
Le piège du rayon et du diamètre
L'une des erreurs les plus classiques survient dès qu'un cercle entre en jeu, que ce soit pour un cylindre, un cône ou une sphère. La confusion entre le rayon (r) et le diamètre (d) est très, très fréquente.
- Le rayon (r), c'est la distance entre le centre du cercle et son contour. C'est la valeur qu'on retrouve dans la plupart des formules de volume, comme V = πr²h pour le cylindre.
- Le diamètre (d), lui, traverse le cercle d'un bord à l'autre en passant par le centre. Il est toujours le double du rayon (d = 2r).
Si un problème vous donne le diamètre, le premier réflexe doit toujours être de le diviser par deux avant de commencer le calcul. Utiliser le diamètre à la place du rayon dans la formule du cylindre, par exemple, peut quadrupler le résultat final! C'est une erreur qui coûte cher.
L'astuce toute simple pour ne pas se tromper? Avant chaque calcul, demandez-vous : « Est-ce que j'utilise bien le rayon? ». Cette simple vérification peut vous sauver bien des maux de tête.
L'oubli des unités au cube
Le volume, c'est une mesure en trois dimensions : on parle de longueur, de largeur et de hauteur. Logiquement, son unité doit refléter ces trois dimensions en étant "au cube".
- Si vos mesures sont en centimètres (cm), le volume sera en centimètres cubes (cm³).
- Si vous mesurez en mètres (m), le volume s'exprimera en mètres cubes (m³).
Oublier l'exposant "3" est une erreur d'inattention très courante sur une copie d'examen. Pensez aussi à vérifier que toutes vos mesures sont dans la même unité avant de les multiplier. On ne mélange jamais des centimètres avec des mètres sans d'abord faire une conversion.
Les erreurs de conversion les plus fréquentes
Savoir jongler avec les unités de volume est une compétence essentielle. Une petite erreur de conversion, et votre résultat devient complètement irréaliste.
Voici les conversions à maîtriser sur le bout des doigts et les pièges à éviter :
- De cm³ à m³ : Attention, on ne divise pas par 100! On divise par 1 000 000 (parce que c'est 100 × 100 × 100). C'est probablement l'erreur la plus courante.
- De cm³ à Litres (L) : La conversion est simple, mais parfois oubliée : 1000 cm³ = 1 L. Imaginez un petit cube de 10 cm de côté; il contient exactement un litre.
- De m³ à Litres (L) : C'est la conversion la plus pratique pour les grands volumes, comme une piscine. 1 m³ = 1000 L. Ne la confondez pas avec la conversion des centimètres cubes!
Une bonne technique pour vous vérifier est de faire une petite estimation. Si vous calculez le volume d'une piscine et que vous obtenez 50 litres, votre bon sens devrait vous alerter. Il y a probablement une erreur de conversion quelque part. Cette logique simple est votre meilleure alliée pour repérer vos propres erreurs.
Questions fréquentes sur la formule du volume
Même après avoir exploré les différentes formes et leurs calculs, il est tout à fait normal que certaines questions subsistent. Cette section est justement là pour dissiper les derniers doutes et consolider votre compréhension de la formule du volume.
Nous avons rassemblé ici les interrogations les plus courantes pour y apporter des réponses claires, directes et faciles à retenir. L'objectif est simple : vous donner la confiance nécessaire pour aborder n'importe quel problème de volume sans la moindre hésitation.
Quelle est la différence entre le volume et l'aire?
C'est une confusion très fréquente, mais la distinction devient limpide une fois qu'on la visualise. En fait, l'aire et le volume ne mesurent pas du tout la même chose.
L'aire mesure une surface plane, en deux dimensions (2D). Imaginez que vous peignez un mur ou que vous déroulez du gazon sur un terrain. On la calcule souvent en multipliant une longueur par une largeur, et son unité est toujours « au carré » (comme les mètres carrés, m²).
Le volume, de son côté, mesure l'espace qu'un objet occupe en trois dimensions (3D). Pensez à la quantité d'eau nécessaire pour remplir une piscine. Il fait intervenir la longueur, la largeur et la hauteur. Son unité est donc « au cube » (comme les mètres cubes, m³).
Pour faire simple, l'aire est une surface, le volume est un espace. L'un recouvre, l'autre remplit.
Pourquoi y a-t-il un « 1/3 » dans la formule du cône?
Cette fameuse fraction de « 1/3 » dans la formule du volume d'un cône ou d'une pyramide n'est pas là par hasard. Elle illustre une relation géométrique à la fois fascinante et très élégante.
Imaginez un cône et un cylindre qui partagent exactement la même base circulaire et la même hauteur. Si vous remplissiez le cône de sable et que vous le versiez dans le cylindre, vous remarqueriez qu'il faudrait le faire trois fois pour remplir complètement le cylindre.
Le volume du cône est donc précisément un tiers de celui du cylindre équivalent. C'est un principe fondamental démontré il y a des siècles qui simplifie énormément nos calculs aujourd'hui.
Comment convertir facilement des mètres cubes en litres?
Savoir passer des mètres cubes (m³) aux litres (L) est une compétence très pratique au quotidien, que ce soit pour un aquarium, une piscine ou une recette. Heureusement, la conversion est l'une des plus simples à mémoriser.
La règle d'or est la suivante :
- 1 mètre cube (m³) = 1000 litres (L)
Pour convertir des mètres cubes en litres, il suffit donc de multiplier le nombre par 1000. Par exemple, un réservoir d'eau de pluie de 2 m³ peut contenir exactement 2 × 1000 = 2000 litres.
Inversement, pour passer des litres aux mètres cubes, on divise par 1000. Une piscine de 50 000 litres a donc un volume de 50 000 ÷ 1000 = 50 m³. C'est une conversion essentielle dans bien des situations pratiques.
La maîtrise de ces concepts est un excellent atout. Mais si vous ou votre enfant avez besoin d'un accompagnement plus personnalisé, n'hésitez pas à demander de l'aide. Pour discuter de vos besoins spécifiques avec des experts, vous pouvez toujours nous contacter pour trouver le bon tuteur.
Un tuteur qualifié peut transformer des difficultés en réussites durables. Chez Centretudes, nous proposons un soutien scolaire personnalisé qui s'adapte au rythme de chaque élève pour renforcer sa confiance et ses compétences. Visitez notre site pour en savoir plus.


