Additionner des fractions, c'est tout simplement combiner des morceaux d'un même tout. Pour y arriver, il y a une règle d'or : s'assurer que toutes les fractions ont le même dénominateur. Autrement dit, il faut que les parts qu’on assemble soient de la même taille. Une fois que c’est fait, le reste est un jeu d'enfant : on additionne les numérateurs, et c’est réglé.
Pourquoi additionner des fractions semble compliqué
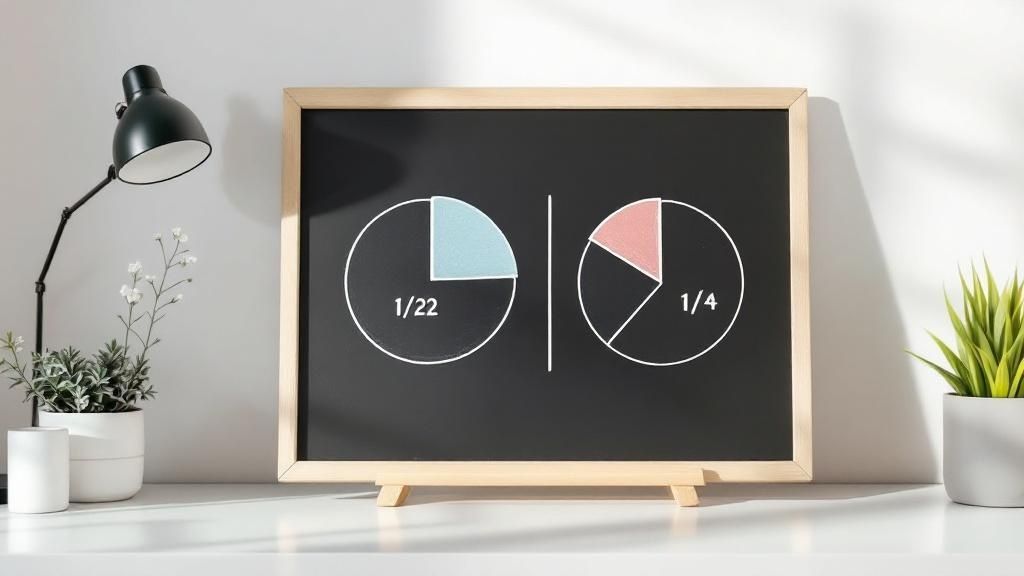
Au premier abord, l'addition de fractions peut paraître intimidante. Elle ne suit pas la même logique que celle des nombres entiers. On ne peut pas juste faire 1/2 + 1/4 et obtenir 2/6. Mais pourquoi? La réponse se cache dans la signification même d'une fraction.
Imaginez une pizza. Le chiffre du bas, qu’on appelle le dénominateur, vous dit en combien de parts égales la pizza est coupée. Le chiffre du haut, le numérateur, indique combien de ces parts vous appartiennent.
Additionner 1/2 pizza et 1/4 de pizza, c'est comme essayer de mettre ensemble des pointes de tailles complètement différentes. Pour savoir ce que vous avez au total, il faut d’abord trouver un moyen de les comparer.
Le concept clé du dénominateur commun
La solution est de trouver une « taille de part commune ». C'est exactement ça, le fameux dénominateur commun. Dans notre exemple, on peut simplement couper la moitié de la pizza (1/2) en deux parts plus petites pour obtenir 2/4. Et voilà, vos parts sont maintenant de la même taille! Vous pouvez alors additionner vos 2/4 avec l'autre 1/4 pour un total de 3/4 de la pizza.
La règle de base est simple : pour additionner des choses, elles doivent être de même nature. Que ce soit des pommes, des dollars ou des parts de gâteau, le principe ne change pas. Trouver un dénominateur commun, c’est simplement s’assurer qu’on additionne des morceaux de taille identique.
D'ailleurs, cette compétence est solidement acquise dès le primaire. Au Québec, par exemple, les données montrent qu'entre 2015 et 2022, plus de 80 % des élèves de 5e année réussissaient à additionner des fractions avec des dénominateurs différents. Si vous voulez en savoir plus sur les approches pédagogiques québécoises, vous pouvez consulter cette ressource éducative d'Alloprof.
En maîtrisant cette idée fondamentale, tout le processus technique devient beaucoup plus logique. Vous n'appliquez plus une formule à l'aveugle; vous comprenez vraiment ce qui se passe derrière les chiffres.
L'addition facile : quand les dénominateurs sont identiques

Pour bien maîtriser l’addition des fractions, commençons par le scénario le plus simple : celui où les dénominateurs sont les mêmes. C'est le point de départ idéal, car la logique est très intuitive et vous donnera la confiance nécessaire pour aborder des cas plus complexes.
Imaginez une tablette de chocolat coupée en 8 carrés. Si vous en avez déjà 2/8 et qu’un ami vous offre 3/8 de plus, vous savez instinctivement que vous avez maintenant 5 carrés sur les 8 au total, soit 5/8. C'est aussi simple que ça!
La règle d’or à retenir est donc très directe. Lorsque les dénominateurs sont identiques, on se concentre uniquement sur les numérateurs.
- On additionne les numérateurs (les chiffres du haut).
- On garde le même dénominateur (le chiffre du bas).
La règle appliquée à un exemple
Mettons cette règle en pratique. Disons que nous voulons calculer 2/9 + 5/9. Ici, le dénominateur commun est 9, ce qui veut dire que toutes nos « parts » sont de la même taille.
On additionne simplement les numérateurs : 2 + 5 = 7. Le dénominateur, lui, reste inchangé. Le résultat final est donc 7/9. C'est une étape cruciale pour comprendre comment additionner des fractions en général, car elle pose les bases.
Pour vous aider à visualiser, voici un tableau récapitulatif de la marche à suivre.
Résumé pour l'addition avec dénominateurs identiques
| Étape | Action | Exemple pour 2/9 + 5/9 |
|---|---|---|
| 1. Vérifier | Confirmer que les dénominateurs sont identiques. | Les deux fractions ont un dénominateur de 9. |
| 2. Additionner | Additionner uniquement les numérateurs. | 2 + 5 = 7 |
| 3. Conserver | Garder le dénominateur commun sans le modifier. | Le dénominateur reste 9. |
| 4. Résultat | Combiner le nouveau numérateur et le dénominateur. | Le résultat final est 7/9. |
Ce tableau illustre bien que le processus est direct et logique lorsque les parts sont de même taille.
Le dénominateur nous dit en combien de parts l'entier est divisé; il ne représente pas une quantité à additionner. L'une des erreurs les plus fréquentes est d'additionner aussi les dénominateurs. Garder ce chiffre intact est la clé!
Enfin, prenez l'excellente habitude de toujours vérifier si votre fraction peut être simplifiée. Après chaque calcul, posez-vous la question. Par exemple, si vous obtenez 4/8, vous remarquerez que le numérateur et le dénominateur peuvent tous deux être divisés par 4. La réponse simplifiée, plus propre, serait 1/2. Cette petite vérification finale assure que votre réponse est toujours sous sa forme la plus simple.
Trouver le dénominateur commun pour tout additionner
On arrive maintenant au cœur du sujet : comment additionner des fractions qui n'ont pas le même dénominateur? C'est souvent là que les choses se corsent un peu, mais rassurez-vous, une fois que la logique est comprise, ça devient un vrai jeu d'enfant. Essayer d'additionner 1/2 et 1/3 directement, c'est comme essayer de comparer des pommes et des oranges; les parts ne sont tout simplement pas de la même taille.
La clé, c'est de trouver un terrain d'entente pour nos fractions. Ce terrain d'entente, c'est ce qu'on appelle le dénominateur commun. Pour le dénicher, la méthode la plus sûre est de trouver le Plus Petit Commun Multiple (PPCM) des dénominateurs.
Cette image illustre parfaitement comment on peut transformer des fractions pour les faire « parler le même langage ». Par exemple, 1/3 et 2/5 deviennent 11/15 une fois qu'on les a mises sur le même dénominateur.
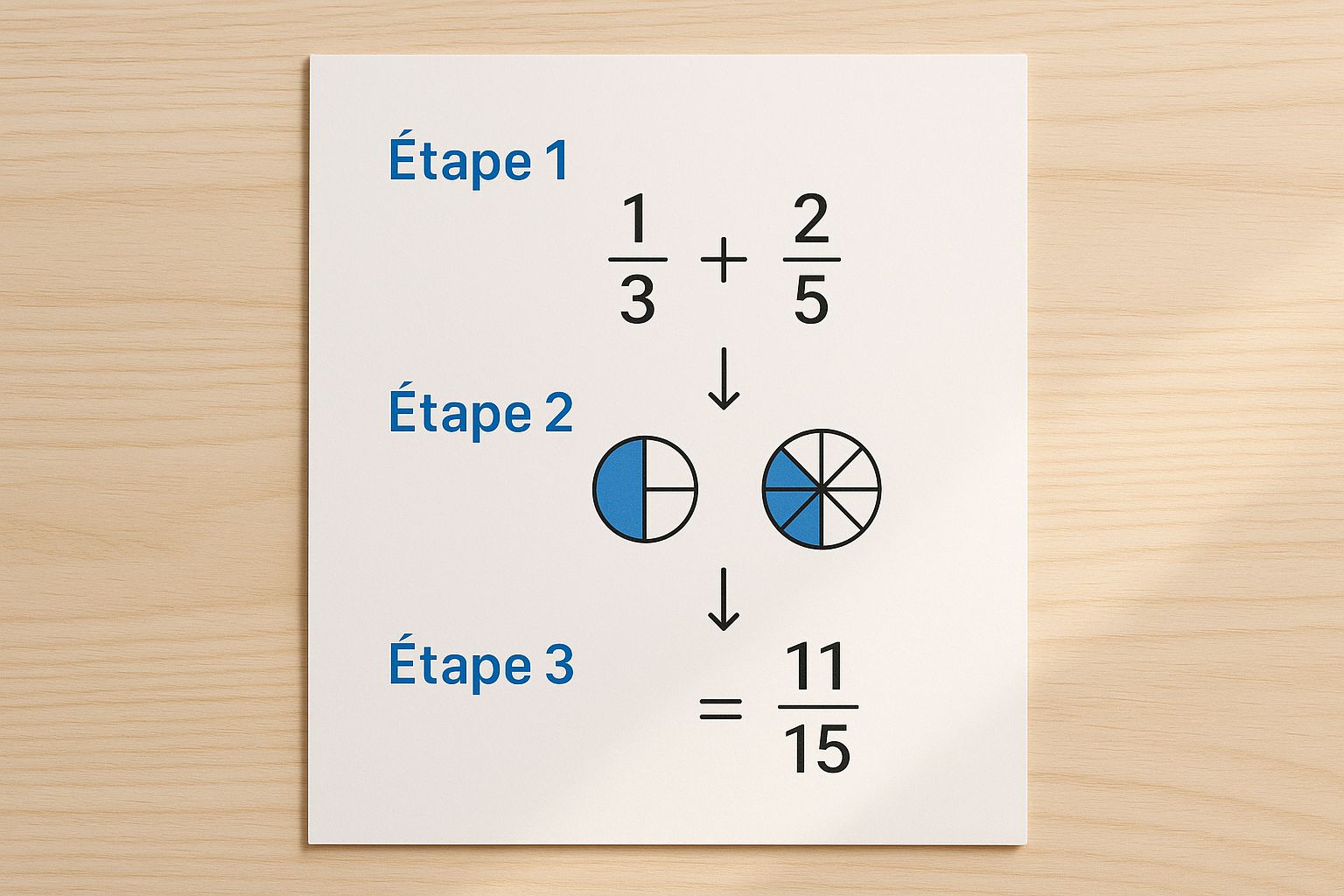
En trouvant ce fameux dénominateur commun (15, dans ce cas), on peut convertir chaque fraction en une version équivalente et l'addition devient un jeu d'enfant.
Identifier le plus petit commun multiple
Le PPCM, c'est tout simplement le plus petit nombre qui est un multiple de tous vos dénominateurs. Prenons un exemple concret avec l'opération 2/3 + 1/4. Ici, nos dénominateurs sont 3 et 4. Pour trouver leur PPCM, on peut lister leurs multiples :
- Multiples de 3 : 3, 6, 9, 12, 15, 18…
- Multiples de 4 : 4, 8, 12, 16, 20…
Le premier nombre qui apparaît dans les deux listes est 12. C'est notre PPCM, notre dénominateur commun magique! Pour aller plus vite, une bonne maîtrise des critères de divisibilité peut vraiment vous donner une longueur d'avance.
Une fois ce chiffre en poche, il ne reste plus qu'à transformer chaque fraction pour qu'elle ait ce nouveau dénominateur, sans bien sûr changer sa valeur.
Transformer les fractions en versions équivalentes
Pour transformer 2/3 en une fraction sur 12, la question à se poser est : « Par quoi dois-je multiplier 3 pour obtenir 12? » La réponse est 4. Pour que la fraction garde la même valeur, on doit multiplier le numérateur ET le dénominateur par ce même nombre.
- Pour la première fraction : (2 × 4) / (3 × 4) = 8/12
On applique le même raisonnement pour la deuxième fraction, 1/4. Pour passer de 4 à 12, on multiplie par 3.
- Pour la seconde fraction : (1 × 3) / (4 × 3) = 3/12
L'astuce, c'est de réaliser que multiplier par 4/4 ou 3/3 revient à multiplier par 1. Vous ne changez donc jamais la valeur de la fraction, juste son apparence. C'est le secret pour réussir toutes vos additions de fractions!
Et voilà! Notre problème de départ, 2/3 + 1/4, s'est transformé en 8/12 + 3/12. On est revenu à une simple addition de fractions avec le même dénominateur.
Il suffit maintenant d'additionner les numérateurs : 8 + 3 = 11. Le résultat final est donc 11/12. C'est aussi simple que ça.
Gérer les nombres fractionnaires et autres cas pratiques
Une fois qu’on maîtrise les dénominateurs communs, l’addition des fractions devient beaucoup plus intéressante. On rencontre rapidement des cas un peu plus complexes, comme les nombres fractionnaires, qui mélangent un nombre entier et une fraction. Imaginez une recette qui demande 2 ½ tasses de farine, puis un ajout de 1 ¾ tasse. Comment on fait pour savoir le total?
La bonne nouvelle, c’est que les techniques que vous connaissez déjà s’appliquent toujours. Ces scénarios plus avancés ne sont que des variations des mêmes principes de base.
Additionner des nombres fractionnaires
Pour additionner des nombres comme 2 ½ + 1 ¾, il y a deux approches principales. Chacune a ses avantages, tout dépend de la situation et de ce que vous préférez.
Approche 1 : Séparer les entiers et les fractions
Cette méthode est souvent la plus facile à visualiser. Ça se passe en deux temps :
- On additionne d’abord les nombres entiers : Dans notre exemple, c’est simple, 2 + 1 = 3.
- Ensuite, on s’occupe des fractions : Il faut calculer ½ + ¾. Le dénominateur commun est 4, donc on transforme ½ en 2/4. L’opération devient 2/4 + 3/4 = 5/4.
- On combine les deux résultats : On a donc 3 et 5/4. Puisque 5/4 est une fraction impropre (qui vaut 1 et ¼), on doit l’ajouter au total des entiers. Le calcul final est donc 3 + 1 ¼ = 4 ¼.
C'est une excellente façon de voir les quantités, mais ça demande une étape de plus si la somme des fractions dépasse 1.
Approche 2 : Convertir en fractions impropres
Cette seconde technique est souvent plus directe et limite les risques d'oubli. L'idée est de tout transformer en fractions impropres avant même de commencer à additionner.
Un nombre fractionnaire, c’est simplement un entier et une fraction collés ensemble. Pour le convertir, on multiplie l’entier par le dénominateur, on ajoute le numérateur, et ce résultat devient le nouveau numérateur.
Appliquons ça à notre exemple :
- Pour 2 ½ : (2 × 2) + 1 = 5. La fraction impropre est 5/2.
- Pour 1 ¾ : (1 × 4) + 3 = 7. La fraction impropre est 7/4.
Le problème devient alors une simple addition de fractions : 5/2 + 7/4. Avec un dénominateur commun de 4, ça se transforme en 10/4 + 7/4 = 17/4. Si on reconvertit ce résultat en nombre fractionnaire (17 divisé par 4), on obtient bien 4 avec un reste de 1, c’est-à-dire 4 ¼.
Autres situations courantes
La beauté de l’addition des fractions, c’est que c’est très polyvalent. On peut aussi bien additionner plus de deux fractions en même temps. La méthode ne change pas : on trouve un dénominateur commun (le PPCM) pour toutes les fractions, on les convertit, puis on additionne tous les numérateurs. Facile!
Et si vous devez additionner une fraction avec un nombre entier, comme 3 + 2/5? C’est encore plus simple que ça en a l’air. Il suffit de se rappeler que n’importe quel nombre entier peut s’écrire comme une fraction sur 1.
- Le nombre 3 devient donc la fraction 3/1.
Votre opération est maintenant 3/1 + 2/5. En utilisant 5 comme dénominateur commun, vous obtenez 15/5 + 2/5, ce qui donne un résultat de 17/5. Ces principes de base s’appliquent aussi à d’autres opérations; pour aller plus loin, jetez un œil à notre guide sur comment diviser des fractions, qui s'appuie sur des concepts très similaires.
Astuces et erreurs courantes à éviter
Maîtriser l’addition de fractions est une chose, mais connaître les pièges courants vous fera gagner un temps précieux. C’est souvent dans les détails que les erreurs se glissent, transformant un calcul simple en un véritable casse-tête.
L’erreur la plus fréquente, et de loin, est d’additionner les dénominateurs entre eux. Si vous devez calculer 1/4 + 2/4, il est très tentant de répondre 3/8. Mais rappelez-vous que le dénominateur indique la taille des parts, pas leur nombre. Vous combinez des quarts de gâteau, vous n'obtenez pas soudainement des huitièmes!
Ne jamais additionner les dénominateurs! C'est la règle d'or qui permet d’éviter 90 % des erreurs classiques. Pensez au dénominateur comme à une unité de mesure; il doit rester le même quand vous additionnez les quantités (les numérateurs).
Simplifier systématiquement le résultat
Une autre bonne habitude à prendre est de toujours vérifier si votre résultat final peut être simplifié. Présenter une fraction comme 6/8 est techniquement correct, mais 3/4 est plus propre et souvent exigé. C'est un peu comme faire le ménage dans ses calculs.
Les études montrent que les difficultés persistent souvent à cause d’une mauvaise compréhension des fractions équivalentes et de l'oubli de simplifier. C'est pourquoi les approches pédagogiques plus visuelles et interactives sont si efficaces pour renforcer ces compétences. Pour mieux comprendre ces méthodes, vous pouvez découvrir les stratégies d’apprentissage sur Alloprof.
Raccourcis utiles et quand les utiliser
Certaines astuces peuvent vraiment accélérer vos calculs. Par exemple, pour additionner 1/3 + 5/6, un coup d'œil rapide suffit pour voir que 6 est un multiple de 3. Pas besoin de chercher plus loin, votre dénominateur commun est 6.
- Vérification rapide : Avant de vous lancer dans la recherche d'un PPCM, vérifiez toujours si l'un des dénominateurs est un multiple de l'autre.
- Multiplication croisée : Pratique pour des petits dénominateurs (par exemple, 2/3 + 4/5), mais attention. Cette technique peut générer de très grands nombres, ce qui compliquera la simplification à la fin.
Éviter ces erreurs communes demande de la pratique et de l'attention. Si ces concepts vous semblent encore un peu flous, un accompagnement personnalisé peut tout changer. Le tutorat en mathématiques permet de cibler précisément ces difficultés pour bâtir une confiance solide.
Vos questions fréquentes sur l'addition des fractions
Même avec de la pratique, il est tout à fait normal que certaines questions persistent. C'est le signe que vous cherchez vraiment à comprendre! Nous avons rassemblé ici les interrogations les plus courantes pour vous donner des réponses claires et directes, de quoi consolider vos nouvelles compétences.
Doit-on absolument trouver le plus petit dénominateur commun?
Non, ce n'est pas une obligation, mais c'est fortement recommandé. En réalité, n'importe quel dénominateur commun fera l'affaire. Une astuce rapide, par exemple, est de simplement multiplier les deux dénominateurs ensemble. Ça fonctionne à tous les coups.
Cependant, prendre le temps de trouver le plus petit commun multiple (le fameux PPCM) vous simplifiera grandement la vie. Vous jonglerez avec des nombres plus petits, ce qui diminue les risques d'erreurs de calcul et rend la simplification de la fraction finale beaucoup plus facile.
C'est un peu comme choisir le bon outil. On peut toujours se débrouiller avec une clé ajustable, mais une clé à la bonne taille est tellement plus efficace et sécuritaire. Le PPCM, c'est la clé parfaitement ajustée pour vos fractions.
Comment faire pour additionner une fraction avec un nombre entier?
Cette situation peut sembler intimidante, mais elle est plus simple qu'il n'y paraît. L'astuce consiste à transformer le nombre entier en une fraction. Comment? En lui donnant tout simplement un dénominateur de 1.
Par exemple, le nombre 3 devient la fraction 3/1. Votre calcul, disons 3 + 2/5, se transforme alors en 3/1 + 2/5. À partir de là, vous êtes en terrain connu! Il suffit d'appliquer la méthode habituelle pour les fractions avec des dénominateurs différents.
Mon résultat est une fraction impropre. Est-ce un problème?
Pas du tout! Une fraction impropre, où le numérateur est plus grand que le dénominateur (comme 7/4), est une réponse tout à fait correcte d'un point de vue mathématique.
Toutefois, pour mieux se représenter la quantité, il est souvent plus parlant de la convertir en nombre fractionnaire (ici, ça donnerait 1 ¾). Pour y arriver, il suffit de diviser le numérateur par le dénominateur. Le résultat de la division (le quotient) est votre nombre entier, et le reste devient le nouveau numérateur, tout en gardant le même dénominateur.
Pour rendre l'apprentissage plus léger et interactif, n'hésitez pas à utiliser des questions brise-glace sur les maths. C'est une excellente façon de lancer la discussion et de dédramatiser les difficultés.
Pourquoi est-ce qu'on n'additionne jamais les dénominateurs?
C'est une excellente question qui touche au cœur même de ce que sont les fractions. Le dénominateur, c'est la taille des parts, pas leur nombre. Si vous additionnez une demi-pizza (1/2) et une pointe de pizza (1/4), vous n'obtenez pas 2/6 de pizza. Les parts n'ont tout simplement pas la même grosseur! On doit d'abord les « couper » en parts de taille égale (le dénominateur commun) avant de pouvoir les compter ensemble.
Si l'addition de fractions demeure un défi, un coup de pouce personnalisé peut faire toute la différence. Chez Centretudes, nos tuteurs certifiés aident votre enfant à bâtir sa confiance et à vraiment maîtriser ces concepts essentiels.
Découvrez nos services de tutorat en mathématiques sur centretudes.ca


