L'aire d'un rectangle, c'est tout simplement l'espace qu'il occupe sur une surface plane. Pour la calculer, la formule est d'une simplicité désarmante : il suffit de multiplier sa longueur par sa largeur. Que ce soit pour planifier des rénovations ou pour réussir un exercice de géométrie, maîtriser ce calcul est un atout indispensable.
Visualiser et comprendre le calcul de l'aire

Calculer l’aire d’un rectangle, c'est un peu comme compter les carreaux de céramique nécessaires pour couvrir un plancher. Imaginez que chaque carreau mesure un mètre carré. L'aire vous dira exactement combien de carreaux il vous faut pour remplir tout l'espace sans laisser le moindre vide. C'est aussi simple que ça!
Cette notion est l'une des pierres angulaires de la géométrie, enseignée depuis des siècles. Ce n'est pas pour rien que la grande majorité des élèves maîtrise ce calcul à la fin du primaire; c'est une compétence de base fondamentale.
La formule clé à retenir est : Aire = Longueur × Largeur. C'est l'unique outil dont vous aurez besoin pour commencer.
Cette approche visuelle rend la formule beaucoup moins abstraite et la transforme en une application concrète et facile à saisir. Pour les élèves qui trouvent les concepts mathématiques un peu plus ardus, un coup de pouce peut faire toute la différence. Des services de tutorat en mathématiques peuvent aider à solidifier ces bases de manière personnalisée et efficace.
Que ce soit pour un projet de bricolage, de jardinage ou simplement pour aider aux devoirs, comprendre comment calculer l'aire d'un rectangle est une compétence pratique et accessible à tous.
Comment appliquer la formule de l'aire étape par étape
Calculer l'aire d'un rectangle peut sembler simple, mais comme souvent en maths, la rigueur est la clé. Le processus est logique et se déroule en quelques étapes faciles à suivre. Le point de départ, bien sûr, est d'identifier les deux mesures dont on a besoin : la longueur et la largeur du rectangle.
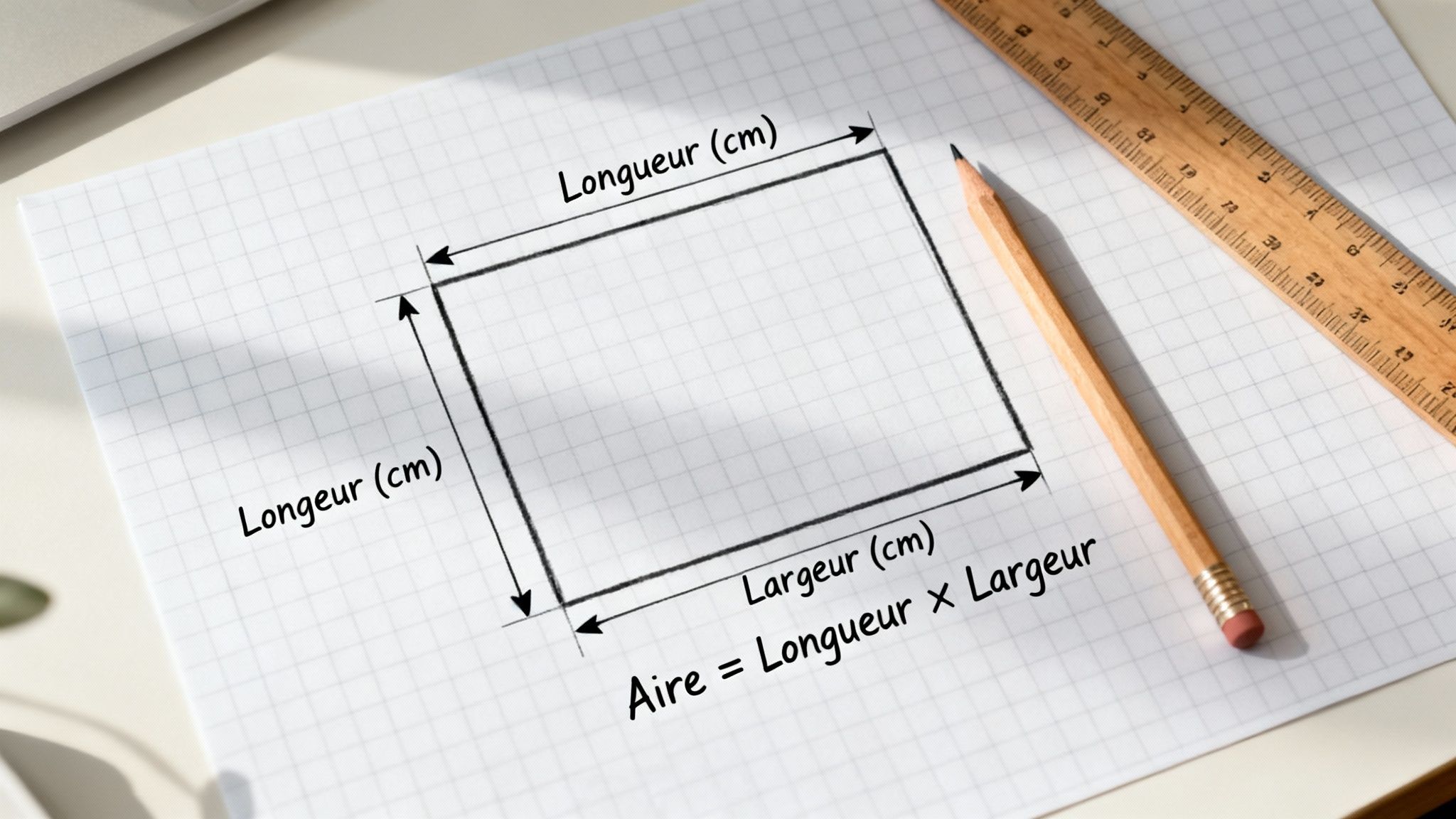
Mais attention, avant de se lancer dans la multiplication, il y a une vérification super importante à faire. Les unités de mesure doivent être les mêmes! Si la longueur est en mètres (m) et la largeur en centimètres (cm), on ne peut pas les multiplier directement. Il faut d'abord tout convertir dans la même unité pour éviter les erreurs.
Une fois que tout est dans la même unité, le plus dur est fait. Il ne reste plus qu'à appliquer la fameuse formule : Aire = Longueur × Largeur.
Un exemple concret pour bien comprendre
Prenons un rectangle tout simple pour illustrer le calcul. Suivez le guide :
- On mesure les côtés : Disons qu'on a un rectangle avec une longueur de 8 cm et une largeur de 5 cm.
- On vérifie les unités : Les deux sont en centimètres. C'est parfait, on peut continuer.
- On applique la formule : On multiplie la longueur par la largeur. Le calcul est donc 8 cm × 5 cm.
- On trouve le résultat : Le produit de 8 par 5, c'est 40.
Le chiffre 40 est correct, mais il manque quelque chose d'essentiel : l'unité. Quand on multiplie des centimètres par des centimètres, le résultat s'exprime en centimètres carrés (cm²).
L'aire de notre rectangle est donc de 40 cm². Le petit exposant "²" est là pour nous rappeler qu'on mesure une surface, et non une simple ligne droite.
Cette notation en unités carrées est fondamentale. Elle nous aide à visualiser que la surface de notre rectangle pourrait être recouverte par exactement 40 petits carrés de 1 cm de côté. C'est ça, l'aire : l'espace à l'intérieur de la figure.
Si ces notions semblent encore un peu floues pour votre enfant, un accompagnement personnalisé peut faire toute la différence. Le tutorat et l'aide aux devoirs en mathématiques sont des outils puissants pour transformer les difficultés en confiance et en réussite. En suivant une méthode claire et structurée, le calcul d'aire deviendra un jeu d'enfant.
Calculer l'aire avec des exemples concrets
La théorie, c’est bien beau, mais rien ne vaut la pratique pour vraiment comprendre. Mettre la formule de l'aire d'un rectangle en application avec des chiffres réels est le meilleur moyen de solidifier ses connaissances.
Voyons ensemble quelques scénarios, du plus simple au plus complexe, pour voir comment tout ça fonctionne.

Exemple 1 : La surface d'un jardin
Imaginez que vous voulez installer une nouvelle pelouse dans votre jardin. La parcelle à couvrir mesure 10 mètres de long par 5 mètres de large. Le calcul est très simple.
- Longueur = 10 m
- Largeur = 5 m
- Calcul : 10 m × 5 m = 50 m²
Vous aurez donc besoin de 50 mètres carrés de gazon pour recouvrir toute la surface. Facile, non?
Exemple 2 : L'aire d'un livre de lecture
Maintenant, ajoutons un petit défi avec des nombres à virgule. Prenons un livre qui mesure 21,5 centimètres de longueur et 15,2 centimètres de largeur. La formule ne change pas, il faut juste être un peu plus vigilant avec la multiplication.
- Longueur = 21,5 cm
- Largeur = 15,2 cm
- Calcul : 21,5 cm × 15,2 cm = 326,8 cm²
La surface de la couverture du livre est donc de 326,8 cm². C'est le genre de problème typique qu'on retrouve à l'école, où la précision est essentielle. Pour les jeunes qui se préparent à des évaluations importantes, maîtriser ce type de calcul est un atout majeur. D'ailleurs, une bonne préparation aux examens ministériels de 6e année aide souvent à bâtir cette confiance.
Le plus grand défi avec les décimales n'est pas la formule, mais l'exactitude du calcul. Il est toujours bon de vérifier son résultat une seconde fois.
Exemple 3 : Gérer la conversion des unités
Voici une situation qui peut causer des maux de tête : quand les unités de mesure ne sont pas les mêmes. Disons que vous avez une table de 150 centimètres de long et 0,8 mètre de large. Attention, on ne peut pas multiplier 150 par 0,8 directement!
Il faut d'abord tout mettre dans la même unité. Le plus simple est souvent de tout convertir en mètres, en se rappelant que 100 cm = 1 m.
- Conversion de la longueur : 150 cm ÷ 100 = 1,5 m.
- Application de la formule : 1,5 m × 0,8 m = 1,2 m².
L'aire de la table est donc de 1,2 mètre carré. Cette petite étape de conversion est cruciale; sans elle, le résultat serait complètement faux.
L’utilité du calcul de l'aire dans la vie de tous les jours
Loin d'être une simple formule mathématique perdue dans un cahier d'école, le calcul de l'aire d'un rectangle est un outil que vous utilisez probablement bien plus souvent que vous ne le pensez. C'est une compétence vraiment pratique qui transforme des idées de projets en plans d'action concrets, avec un budget et des quantités précises.
Que vous soyez en train de planifier des rénovations ou de simplement réaménager votre jardin, ce calcul est partout. Il vous aide à prendre des décisions éclairées et à éviter de gaspiller du temps ou de l'argent.
Des applications concrètes à la maison
Les exemples les plus parlants se trouvent directement chez vous. Pensez à toutes ces fois où vous avez eu besoin d'estimer une surface :
- Peinturer un mur : En calculant l'aire du mur, vous saurez exactement combien de pots de peinture acheter. Fini les allers-retours inutiles à la quincaillerie!
- Poser un nouveau plancher : Connaître la superficie de la pièce est indispensable pour commander la bonne quantité de bois franc, de céramique ou de tapis.
- Aménager le jardin : Pour acheter la bonne quantité de gazon en rouleaux ou de paillis, le calcul de l'aire de la zone à couvrir est la toute première étape.
- Visiter un appartement : Calculer rapidement la superficie d'une pièce vous donne une idée beaucoup plus réaliste de l'espace, bien au-delà de ce que l'annonce prétend.
Cette compétence devient vite un réflexe pour mieux gérer les projets du quotidien. Si ces applications semblent un peu complexes à expliquer à votre enfant, un service d'aide aux devoirs et de soutien scolaire peut les rendre plus concrètes et amusantes.
Le calcul de l'aire n'est pas seulement utile pour les particuliers. Il est au cœur de nombreux métiers comme l'architecture, l'urbanisme et l'immobilier, où la précision des surfaces est absolument primordiale.
Même à plus grande échelle, ce concept est essentiel. En France, l’INSEE utilise un système de quadrillage basé sur des rectangles pour uniformiser la collecte de données démographiques et géographiques. Pour les curieux, tous les détails sur cette méthode de carroyage statistique se trouvent sur insee.fr.
Éviter les erreurs de calcul les plus courantes
Même avec une formule aussi simple que celle de l'aire d'un rectangle, quelques pièges classiques peuvent facilement fausser le résultat. Le meilleur moyen de ne pas tomber dedans, c'est de bien les connaître pour les anticiper.
Le premier obstacle, et de loin le plus fréquent, est le mélange des unités de mesure. Multiplier des centimètres avec des mètres, par exemple, est une erreur qui garantit un résultat complètement à côté de la plaque. La règle d'or est simple : avant de commencer le moindre calcul, on s'assure que la longueur et la largeur sont bien exprimées dans la même unité.
Une autre confusion qui revient souvent est de mélanger l'aire et le périmètre. Ce sont deux concepts très différents! Le périmètre, c'est la mesure du contour de la figure (on additionne les côtés), alors que l'aire mesure la surface à l'intérieur (on multiplie la longueur par la largeur).
Les trois pièges à déjouer
Pour vous aider à ne plus vous tromper, voici les trois erreurs les plus fréquentes et comment les corriger une bonne fois pour toutes :
- L’oubli de la conversion : Si une mesure est en centimètres (cm) et l'autre en mètres (m), il faut absolument en convertir une avant de multiplier. Pas le choix!
- La confusion aire/périmètre : Pour s'en souvenir, pensez : Aire = multiplication, Périmètre = addition. Deux opérations, deux résultats différents.
- L'oubli de l'unité carrée : Le résultat d'un calcul d'aire doit toujours, toujours être en unités carrées (cm², m², etc.). Écrire "50 m" au lieu de "50 m²" n'est pas qu'un détail, ça change complètement le sens de la réponse.
Une petite astuce pour y penser : imaginez que vous posez du carrelage sur le sol. Vous ne calculez pas une simple ligne, mais bien des rangées de carreaux qui couvrent toute la surface. C'est pour ça que le résultat est "carré".
Cette infographie illustre bien à quel point l'aire est utile dans des situations bien réelles, que ce soit pour la peinture, le jardinage ou même l'immobilier.
En visualisant ces applications, on comprend mieux que l'aire est une mesure de surface, ce qui aide énormément à ne plus la confondre avec une simple longueur comme le périmètre.
Questions fréquentes sur le calcul de l'aire
Même avec la formule et les exemples bien en tête, certaines questions pratiques peuvent encore surgir. C'est tout à fait normal. Passons en revue les interrogations les plus courantes pour lever les derniers doutes et vous permettre d'aborder le calcul de l'aire d'un rectangle avec une confiance totale.
Que faire si les unités sont différentes?
Voilà une excellente question, car c'est probablement l'une des sources d'erreurs les plus fréquentes! Si la longueur est en mètres et la largeur en centimètres, par exemple, il est obligatoire de tout convertir dans la même unité avant de faire la multiplication.
Vous avez le choix : soit vous convertissez tout en mètres, soit tout en centimètres. Une fois que c'est fait, vous pouvez appliquer la formule sans risque de vous tromper.
Quelle est la différence entre l'aire et le périmètre?
Il est primordial de ne pas mélanger ces deux notions. L'aire mesure toute la surface qui se trouve à l'intérieur du rectangle, alors que le périmètre ne mesure que la longueur de son contour.
- Aire : On multiplie la longueur par la largeur (L × l). C'est la mesure de l'espace plat.
- Périmètre : On additionne la longueur de tous les côtés (2L + 2l). C'est la mesure du trait qui délimite la forme.
Pour visualiser, pensez à un tapis qui couvre le sol : c'est l'aire. La bordure ou la clôture autour du jardin, c'est le périmètre.
Comment trouver un côté si on connaît l'aire?
Oui, il est tout à fait possible de faire le calcul à l'envers! Si vous connaissez déjà l'aire et la mesure d'un des deux côtés (disons, la largeur), il suffit de faire une simple division. Vous divisez l'aire par la mesure du côté que vous connaissez pour trouver la longueur de l'autre.
La formule s'inverse et devient : Longueur = Aire ÷ Largeur.
Cette petite astuce est très pratique dans bien des problèmes de géométrie. Si d'autres questions plus pointues vous viennent à l'esprit ou si votre enfant a besoin d'un coup de pouce personnalisé, n'hésitez pas à nous contacter pour discuter de ses besoins.
Chez Centrétudes, nous transformons les doutes en confiance grâce à un accompagnement sur mesure. Découvrez comment nos tuteurs peuvent aider votre enfant à réussir en mathématiques. Visitez https://centretudes.ca pour en savoir plus.


