Découvrir l'aire d'un cylindre comme un ami vous l'expliquerait

Imaginez que vous décollez l'étiquette d'une canette de soda. Vous obtenez un rectangle. C'est ce qu'on appelle l'aire latérale du cylindre. Mais pour connaître l'aire totale, il faut aussi penser aux deux cercles qui ferment la canette, en haut et en bas : les bases.
L'aire totale d'un cylindre, c'est donc la somme de ces trois surfaces. Imaginez que vous voulez peindre entièrement cette canette : vous devez connaître son aire totale pour acheter la bonne quantité de peinture. Même chose si vous emballez un cadeau cylindrique : l'aire totale vous dira combien de papier cadeau il vous faut.
Les trois composantes de l'aire d'un cylindre
Pour calculer l'aire d'un cylindre, il faut bien comprendre qu'elle est composée de trois parties : les deux bases circulaires et l'aire latérale (notre étiquette de canette !).
La formule magique
Pour un cylindre droit, on utilise la formule suivante : ( A_{totale} = 2 \times \pi \times r^2 + 2 \times \pi \times r \times h ). Ici, ( r ) représente le rayon des cercles (la moitié du diamètre) et ( h ) la hauteur du cylindre.
Un exemple concret
Prenons un cylindre dont le rayon ( r ) est de 5 cm et la hauteur ( h ) de 10 cm. En appliquant la formule, l'aire totale est d'environ 471,24 cm². Ce genre de calcul est très utile dans plein de domaines, par exemple pour déterminer la surface d'un réservoir cylindrique.
Vous voulez en savoir plus sur les cylindres ? Jetez un coup d'œil à cette page Wikipédia. Et si vous avez besoin d'un coup de pouce en maths, n'hésitez pas à consulter les services de tutorat du Centre Études. Avec une bonne explication et des exemples concrets, l'aire d'un cylindre n'aura plus de secrets pour vous !
Les trois visages cachés de votre cylindre
Imaginez un cylindre. Une boîte de conserve, un rouleau de papier essuie-tout, une colonne grecque… Pour calculer l'aire d'un cylindre, il faut le voir non pas comme un bloc, mais comme l'assemblage de trois surfaces distinctes. Déconstruisez mentalement cette boîte de conserve : vous obtenez deux disques (les bases) et un rectangle (la surface latérale, une fois déroulée).
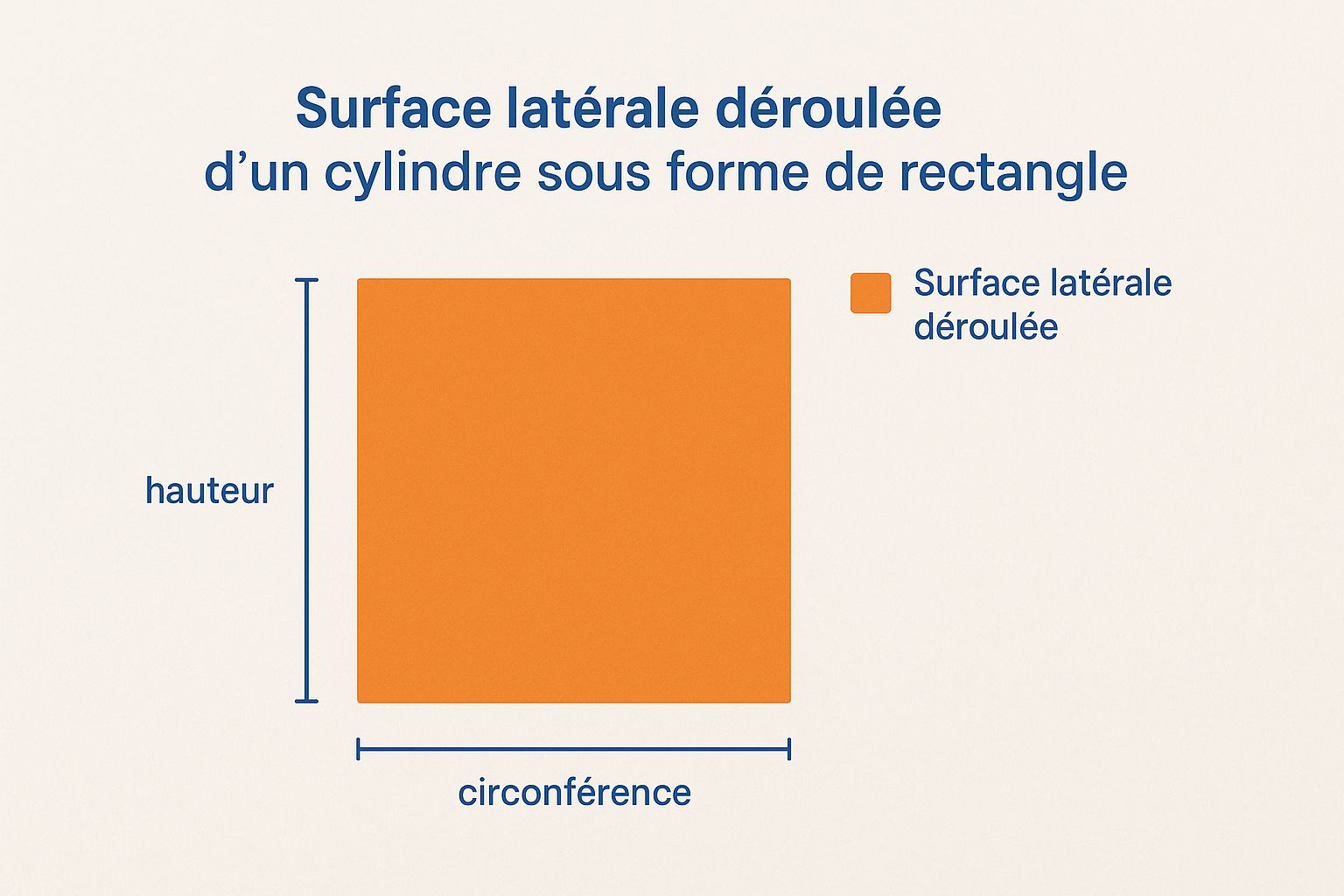
Ce schéma nous montre la surface latérale à plat, révélant sa forme rectangulaire. Remarquez comme la longueur de ce rectangle correspond au périmètre du cercle de base, et sa largeur à la hauteur du cylindre. C'est une image clé pour comprendre la formule de l'aire.
Calcul de l'aire : une addition de trois surfaces
Calculer l’aire totale d’un cylindre revient à additionner l’aire de ces trois surfaces. Commençons par les deux bases circulaires. Leur aire est simple à calculer : πr², où r représente le rayon du cercle.
La surface latérale, quant à elle, est un peu plus subtile. Dépliée, elle forme un rectangle. Sa largeur correspond à la hauteur h du cylindre. Sa longueur, c'est le périmètre du cercle de base, soit 2πr. L'aire de ce rectangle est donc 2πr * h.
La formule magique : 2πr² + 2πrh
L'aire totale du cylindre s'obtient en additionnant l'aire des deux bases et de la surface latérale. On arrive donc à la formule : 2πr² + 2πrh. Gardez cette formule précieusement, c'est la clé pour maîtriser ce calcul.
Pour mieux visualiser, prenons un exemple concret. Imaginons un rouleau de papier essuie-tout. Vous pouvez maintenant calculer son aire en mesurant son rayon et sa hauteur !
Afin de clarifier les différentes composantes de l'aire d'un cylindre, voici un tableau récapitulatif :
Comparaison des trois surfaces du cylindre
Tableau comparant les caractéristiques, formules et exemples de calcul pour chaque surface composant l'aire totale
| Surface | Forme géométrique | Formule | Nombre requis |
|---|---|---|---|
| Base 1 | Cercle | πr² | Rayon (r) |
| Base 2 | Cercle | πr² | Rayon (r) |
| Surface latérale | Rectangle | 2πrh | Rayon (r) et Hauteur (h) |
Ce tableau synthétise les informations essentielles pour calculer l'aire de chaque surface. N'oubliez pas : l'aire totale est la somme de ces trois aires.
Avec ces explications et ce tableau, vous pouvez maintenant aborder le calcul de l'aire d'un cylindre avec confiance. Des tuyaux de plomberie aux colonnes antiques, le monde cylindrique n'a plus de secrets pour vous !
Construire la formule comme un détective résout une énigme

Oublions les formules mathématiques qui semblent parfois sortir de nulle part. Au lieu de les apprendre par cœur, découvrons ensemble, étape par étape, comment construire la formule de l'aire d'un cylindre. Imaginez-vous en Sherlock Holmes des mathématiques, face à un cylindre, avec pour seules armes vos connaissances sur les cercles et les rectangles.
L'aire des bases : parlons cercle
Commençons par les deux bases circulaires de notre cylindre. Rappelez-vous la formule de l'aire d'un cercle : πr², où r représente le rayon. Nos deux bases étant identiques, leur aire totale est simplement le double, soit 2πr². Voilà une première pièce du puzzle !
L'aire latérale : un rectangle caché
Passons maintenant à la surface latérale. Si on l'imagine déroulée, comme une étiquette de conserve, on obtient un rectangle. La largeur de ce rectangle correspond à la hauteur h du cylindre. Et sa longueur ? C'est tout simplement le périmètre du cercle de base, c'est-à-dire 2πr. L'aire de ce rectangle est donc 2πr * h. Nous avons notre deuxième indice !
Assembler les pièces du puzzle : la formule finale
Il ne reste plus qu'à assembler les pièces. L'aire totale du cylindre est la somme de l'aire des deux bases et de l'aire latérale. On obtient donc : Aire d'un cylindre = 2πr² + 2πrh. Vous l'avez construite vous-même, plus besoin de mémorisation arbitraire ! Pour approfondir vos méthodes de travail et d'apprentissage, jetez un coup d'œil à cet article sur l'importance des devoirs.
Visualiser la formule en action
Prenons un exemple concret. Imaginez un rouleau d'essuie-tout. Mesurez son rayon et sa hauteur. Grâce à la formule que nous venons de voir, vous pouvez calculer son aire totale. Et cela fonctionne avec n'importe quel cylindre, d'une canette de soda à un pilier d'architecture. Vous avez maintenant les outils pour décoder les surfaces cylindriques autour de vous.
Maîtriser par la pratique : du café du matin au silo agricole
Imaginez-vous en train d'emballer votre tasse de café du matin avec du papier cadeau. Pour simplifier, on va la considérer comme un cylindre parfait. Vous avez besoin de connaître sa surface pour ne pas gaspiller de papier, n'est-ce pas ? C'est là qu'intervient l'aire du cylindre. Prenez le rayon de l'ouverture (la moitié du diamètre) et la hauteur de votre tasse. La formule magique est 2πr² + 2πrh. Et voilà, vous avez l'aire totale à couvrir !
Maintenant, imaginons quelque chose de plus grand : le réservoir d'eau cylindrique sur le toit de votre immeuble. Si vous devez le repeindre, connaître son aire est essentiel pour estimer la quantité de peinture nécessaire. Même chose pour une colonne décorative : l'aire du cylindre vous indique la surface à recouvrir de stuc, de mosaïque, ou tout autre matériau.
Applications concrètes : des silos aux canettes
Prenons un exemple plus imposant : un silo à grains. Ces structures cylindriques géantes nécessitent un calcul précis de leur aire pour déterminer la quantité de métal à utiliser lors de la construction. Une erreur de calcul, et les coûts supplémentaires peuvent vite grimper ! Une fois la surface connue, il est important de comprendre comment des taxes comme la TVA s'appliquent. Pour en savoir plus, consultez ce lien : calcul de TVA.
Même les objets du quotidien, comme une simple canette de soda, illustrent l'importance de cette notion. Les fabricants optimisent les dimensions des canettes pour utiliser le moins de métal possible et réduire les coûts de production. Chaque millimètre carré compte !
Développer son intuition mathématique
En manipulant ces exemples concrets, vous développerez une intuition mathématique précieuse. Si vous calculez l'aire d'une tasse à café et que vous obtenez un résultat en mètres carrés, votre bon sens vous dira qu'il y a une erreur quelque part ! C'est comme apprendre à "dialoguer" avec les nombres et à comprendre leur signification dans le monde réel.
Si vous avez besoin d'un coup de pouce pour consolider vos connaissances, n'hésitez pas à explorer les ressources disponibles. Des plateformes comme le Centre Études proposent du tutorat en sciences qui peut vous être très utile. L'objectif est de dépasser la simple application de formules et de transformer chaque calcul en une réflexion logique.
Quand les cylindres font partie de notre quotidien
L’aire d’un cylindre, loin d’être une notion abstraite réservée aux cours de mathématiques, est omniprésente dans notre vie de tous les jours. Imaginez une simple canette de soda. Sa forme cylindrique n’est pas un hasard. Les fabricants, comme Coca-Cola, utilisent le calcul de l’aire d’un cylindre pour déterminer la quantité de métal nécessaire à sa fabrication, optimisant ainsi les coûts de production et réalisant des économies substantielles.
Pensez maintenant à l’architecture. Les colonnes, éléments structuraux et esthétiques, sont souvent cylindriques. L’architecte doit connaître leur aire pour estimer la quantité de peinture nécessaire. De même, un agriculteur qui construit un silo à grains doit calculer son aire pour déterminer sa capacité de stockage. Ces exemples illustrent l'importance pratique de ce concept mathématique dans des domaines variés et son impact sur les décisions économiques. D’ailleurs, cette notion est enseignée dès le secondaire, permettant aux élèves d'acquérir des compétences utiles pour résoudre des problèmes concrets. Envie d'en savoir plus ?
Des exemples surprenants
Mais l’influence de l’aire du cylindre ne s’arrête pas là. En design industriel, elle est essentielle pour concevoir des emballages optimisés, des réservoirs performants et des outils ergonomiques. Imaginez la conception d'un nouveau flacon de parfum ou la fabrication d'un piston de moteur : l'aire du cylindre est au cœur du processus. L’architecture moderne, avec ses structures complexes et audacieuses, repose également sur ce calcul précis pour la construction de bâtiments et d'infrastructures. Même l'art contemporain s'en inspire, jouant avec les formes cylindriques pour créer des œuvres originales et captivantes. Et comme pour toute compétence, une bonne communication est essentielle pour bien expliquer et comprendre ces concepts, comme l’explique cet article.
L'accompagnement scolaire : un atout précieux
Le calcul de l’aire d’un cylindre, comme de nombreux concepts mathématiques, peut parfois sembler complexe pour certains élèves. Un accompagnement personnalisé, comme le tutorat, peut s’avérer très bénéfique. Un tuteur peut aider l'élève à visualiser la formule, à la comprendre dans des situations concrètes et à développer son intuition mathématique. Découvrez pourquoi le tutorat peut être une solution intéressante. Il permet de construire une base solide et d’aborder les mathématiques avec plus de confiance.
Éviter les pièges classiques qui piègent tout le monde
Imaginez : vous êtes en plein examen, face à un problème sur l'aire d'un cylindre. Vous avez révisé, vous connaissez la formule… et pourtant, quelque chose cloche. Le résultat semble improbable. C'est le moment où les pièges classiques peuvent vous surprendre. Heureusement, en les connaissant, on peut facilement les éviter.
Les erreurs fréquentes et comment les déjouer
Un oubli fréquent ? Les bases ! On se concentre tellement sur la surface latérale, ce rectangle enroulé, qu'on oublie les deux cercles qui ferment le cylindre. Pensez à une boîte de conserve : on doit prendre en compte le métal du côté et celui des deux couvercles. Visualiser le cylindre comme un objet en 3D, et non juste un tube, est la clé.
Rayon ou diamètre ? Voilà une autre source de confusion. La formule de l'aire latérale utilise le rayon (la moitié du diamètre). Un simple schéma avec les dimensions clairement indiquées peut vous éviter ce piège. En cas de doute, relisez attentivement l'énoncé. Besoin d'un coup de pouce ? Des ressources comme le Centre Études proposent du tutorat et de l'aide aux devoirs en ligne.
Enfin, ne confondez pas aire et volume. L'aire, c'est la surface extérieure, comme la quantité de papier cadeau nécessaire pour emballer le cylindre. Le volume, c'est l'espace à l'intérieur, comme la quantité d'eau qu'il peut contenir. Deux notions distinctes, deux formules différentes.
Voici un tableau récapitulatif pour vous aider à identifier et corriger les erreurs courantes :
Guide de vérification des calculs d'aire de cylindre
Checklist des erreurs communes avec leurs causes, conséquences et méthodes de détection
| Erreur courante | Cause principale | Impact sur le résultat | Méthode de vérification |
|---|---|---|---|
| Oubli de l'aire des bases | Concentration excessive sur l'aire latérale | Aire totale sous-estimée | Visualiser le cylindre en 3D, se rappeler des deux cercles |
| Confusion rayon/diamètre | Inattention à la formule | Aire latérale erronée (trop grande ou trop petite) | Schéma clair avec les dimensions, relecture de l'énoncé |
| Confusion aire/volume | Méconnaissance des concepts | Calcul d'une grandeur inappropriée | Se remémorer la définition de l'aire et du volume |
Ce tableau met en lumière les erreurs fréquentes, leurs causes et surtout, comment les repérer. Gardez-le à portée de main lors de vos exercices !
Adopter les bonnes pratiques
Pour des calculs sans accroc, adoptez ces quelques réflexes :
- Schématisez : Un dessin rapide du cylindre avec ses dimensions annotées clarifie la situation.
- Notez la formule : Avant de remplacer les variables, écrivez la formule complète de l'aire totale.
- Vérifiez l'unité et l'ordre de grandeur : Le résultat est en cm² ou m² ? Semble-t-il cohérent avec les dimensions du cylindre ?
Ces vérifications, comme celles d'un pilote avant le décollage, vous assurent un vol sans turbulences ! Envie d'aller plus loin et de consolider vos acquis ? Centrétudes offre des services de tutorat personnalisés pour vous aider à atteindre vos objectifs. Découvrez leurs services dès maintenant !


