Le cours de calcul différentiel au Cégep est une étape incontournable si vous visez des études en sciences, en génie ou en informatique. C'est bien plus qu'une simple série d'équations; c'est un outil puissant qui vous apprend à décortiquer le changement et le mouvement, posant ainsi les fondations de concepts mathématiques beaucoup plus complexes. Pour réussir, il faut l'aborder avec le bon état d'esprit et de bonnes stratégies.
Pourquoi ce cours est bien plus qu'une simple exigence

Affronter le calcul différentiel, souvent sous des sigles comme 201-NYA-05, peut sembler intimidant. Beaucoup d'étudiants le voient comme un obstacle majeur, mais c'est en réalité une occasion en or de développer le raisonnement logique et analytique qui vous sera essentiel tout au long de votre parcours, tant académique que professionnel.
Imaginez un instant : l'algèbre vous apprend à résoudre des situations figées, statiques. Le calcul, lui, vous donne les outils pour comprendre un monde en perpétuel mouvement. C'est la différence entre prendre une photo et analyser une vidéo, image par image, pour en comprendre la dynamique.
Comprendre la structure du cours
Un cours typique de calcul différentiel au Cégep n'est pas qu'une liste de formules à apprendre par cœur. Il est conçu pour bâtir votre compréhension étape par étape. Voici les piliers sur lesquels repose généralement le cours :
- Les limites et la continuité : C'est le socle sur lequel tout le reste est construit. Ces concepts vous permettent d'explorer comment les fonctions se comportent à une échelle infiniment petite.
- La dérivée : Voilà le cœur du sujet. La dérivée est un outil qui mesure un taux de changement instantané. Pensez à la vitesse exacte d'une voiture à un moment précis, et non sa vitesse moyenne sur un trajet.
- Les applications de la dérivée : C'est ici que la théorie prend tout son sens. Vous apprendrez à optimiser des scénarios, comme maximiser des profits, et à analyser des fonctions pour tracer leurs graphiques avec une précision redoutable.
Chaque année, près de 15 000 étudiants au Québec s'attaquent à ce cours. La structure habituelle, avec ses trois heures de théorie et deux heures de travaux pratiques par semaine, est pensée pour bien assimiler la matière.
Des études ont même montré que des approches comme les tests diagnostiques en début de session permettent d'augmenter le taux de réussite de 5 à 10 % en identifiant rapidement les besoins de chacun.
La réussite en calcul différentiel ne dépend pas d'un supposé "don" pour les maths, mais plutôt de la maîtrise des concepts de base et d'une pratique régulière. Chaque nouvelle idée s'appuie sur la précédente, formant une chaîne logique que vous pouvez tout à fait maîtriser.
Le tableau suivant vous donne une idée plus claire de ce qui vous attend.
Structure typique du cours de calcul différentiel au Cégep
Ce tableau résume les composantes clés et les attentes d'un cours standard de calcul différentiel, comme le 201-SN2-RE ou équivalent.
| Composante | Description | Temps alloué (approx.) |
|---|---|---|
| Limites et continuité | Introduction aux concepts fondamentaux qui sous-tendent la dérivée. | 3 semaines |
| La dérivée | Définition, règles de dérivation (produit, quotient, chaîne) et dérivation implicite. | 5 semaines |
| Applications de la dérivée | Taux liés, problèmes d'optimisation, étude de fonctions et traçage de courbes. | 4 semaines |
| Révision et examens | Périodes dédiées à la consolidation des acquis et aux évaluations. | 3 semaines |
Comme vous pouvez le voir, le cours est progressif. Chaque bloc de matière est une nouvelle brique ajoutée à votre édifice de connaissances.
Adopter la bonne approche dès le départ
Le secret pour non seulement passer ce cours, mais aussi y prendre goût, est d'adopter une approche active. Ne soyez pas un simple spectateur en classe; impliquez-vous. Posez des questions, refaites les exemples du prof et, surtout, ne laissez jamais les difficultés s'accumuler.
Si un concept vous échappe, chercher de l'aide rapidement est la meilleure stratégie possible. Un coup de pouce ciblé peut transformer une notion qui vous semble obscure en un concept parfaitement clair et logique.
Pour solidifier vos compétences, le tutorat en mathématiques est une excellente ressource. Il vous offre un accompagnement personnalisé pour surmonter les défis spécifiques au calcul différentiel au Cégep.
Construire vos fondations sur les limites et la continuité

Avant même de rêver aux dérivées et aux intégrales, il faut s’assurer que les fondations sont solides. En calcul différentiel au Cégep, tout commence avec deux idées maîtresses : les limites et la continuité. Sans bien saisir ces deux concepts, le reste du cours risque de ressembler à un empilement de formules abstraites sans grand sens.
Pensez à une fonction comme à un chemin tracé sur une carte. La limite, c'est un peu comme deviner votre destination exacte en vous approchant infiniment d'un point, sans jamais tout à fait y arriver. On étudie ce qui se passe tout près d’une valeur, pas nécessairement à cette valeur précise.
C’est cette petite nuance qui change tout. Elle nous permet d’analyser des points qui semblent à première vue « impossibles », comme une division par zéro, simplement en regardant comment le chemin se comporte juste à côté.
Visualiser le concept de limite
Imaginez que vous avez une loupe et que vous zoomez sur un point x de votre chemin. La limite, c’est la hauteur y vers laquelle le chemin semble se diriger sans le moindre doute, que le point existe réellement ou pas.
Prenons un exemple concret : la fonction f(x) = (x² – 4) / (x – 2). Si on essaie de voir ce qui se passe quand x s’approche de 2, on frappe un mur. Remplacer x par 2 crée une division par zéro, un interdit en maths. Mais si on triche un peu et qu'on regarde à x = 1,999 ou à x = 2,001, on voit que la valeur de f(x) se rapproche drôlement de 4. La limite est donc 4.
Une limite n'est pas ce que la fonction est à un point, mais ce vers quoi elle tend. C'est une prédiction basée sur son comportement à une échelle infiniment petite.
Le calcul des limites est donc la toute première compétence technique à développer. Heureusement, il existe plusieurs trucs pour déjouer les pièges mathématiques.
Techniques essentielles pour calculer les limites
Au Cégep, vous allez remplir votre coffre à outils avec différentes techniques pour évaluer les limites. Voici les plus importantes :
- La substitution directe : C’est la première chose à essayer, toujours. Si la fonction est bien définie au point qui vous intéresse, il suffit de remplacer la variable par sa valeur. C’est simple et direct.
- La factorisation et la simplification : Quand la substitution vous mène à une forme bizarre comme 0/0, c'est souvent un signe qu'il faut simplifier. Factoriser les polynômes au numérateur et au dénominateur permet très souvent de faire disparaître le problème.
- La rationalisation : Votre meilleure amie quand il y a des racines carrées. On multiplie le haut et le bas par le « conjugué » pour se débarrasser de la racine et simplifier l'expression.
Ces méthodes demandent de la pratique, c’est certain, mais elles sont absolument cruciales. Si vous avez de la difficulté, n’attendez pas. Une aide aux devoirs en mathématiques peut vraiment faire la différence pour bien ancrer ces bases.
Comprendre la continuité, un chemin sans interruption
Après le concept un peu étrange de la limite, celui de la continuité est beaucoup plus facile à visualiser. Une fonction est continue si vous pouvez dessiner son graphique sans jamais avoir à lever votre crayon. Pas de trou, pas de saut, pas de ligne verticale infinie.
De façon plus formelle, une fonction f est continue en un point c si ces trois conditions sont respectées :
- f(c) est défini (le point existe sur le graphique).
- La limite de f(x) quand x tend vers c existe.
- La limite est égale à la valeur réelle : lim f(x) = f(c).
En gros, la continuité, c'est quand la prédiction (la limite) correspond parfaitement à la réalité (la valeur du point). C'est une propriété indispensable, car on ne peut dériver une fonction que là où elle est continue. C'est la garantie que le chemin est « lisse » et prévisible, ce qui nous permettra ensuite de mesurer sa pente à n'importe quel endroit.
Comprendre le pouvoir de la dérivée
La dérivée, c'est le véritable cœur du calcul différentiel au Cégep. Pour vraiment saisir sa puissance, il faut mettre de côté les formules compliquées un instant et la voir pour ce qu'elle est : un outil incroyable pour mesurer un changement à un moment précis.
Pensez au compteur de vitesse de votre voiture. Il n'indique pas votre vitesse moyenne depuis le début de votre trajet, mais bien votre vitesse maintenant. La dérivée fait exactement ça. Elle capture une dynamique instantanée, là où l'algèbre se limite souvent à décrire des situations fixes.
Dans cette section, on va passer de l'intuition à la pratique. On explorera d'abord sa signification géométrique, puis on décortiquera les règles de dérivation qui deviendront vos meilleurs alliés pour analyser n'importe quelle fonction.
La dérivée comme pente de la tangente
Sur un graphique, la dérivée d'une fonction à un point précis, c'est tout simplement la pente de la droite tangente à la courbe à cet endroit. Une droite tangente, c'est une ligne qui vient « frôler » la courbe en un seul point, en suivant exactement sa direction à ce moment-là.
Imaginez que vous marchez le long de la courbe d'une fonction. Si vous vous arrêtez et que vous regardez droit devant, l'inclinaison de votre regard correspond à la valeur de la dérivée.
- Si la pente est positive, la fonction monte à cet endroit.
- Si la pente est négative, la fonction descend.
- Si la pente est nulle, vous êtes sur un sommet ou dans un creux (un extrémum).
Cette idée toute simple est au cœur de plein d'applications, comme trouver les points maximums et minimums d'une fonction, ce qui est super important en optimisation.
La dérivée transforme un problème visuel un peu flou (quelle est l'inclinaison de ma courbe ?) en un calcul bien concret. Elle nous donne un chiffre qui décrit parfaitement comment la fonction se comporte localement.
Cette infographie montre bien la différence entre le taux de changement moyen, qui calcule la pente sur un intervalle, et la dérivée, qui mesure la pente instantanée en un point unique.
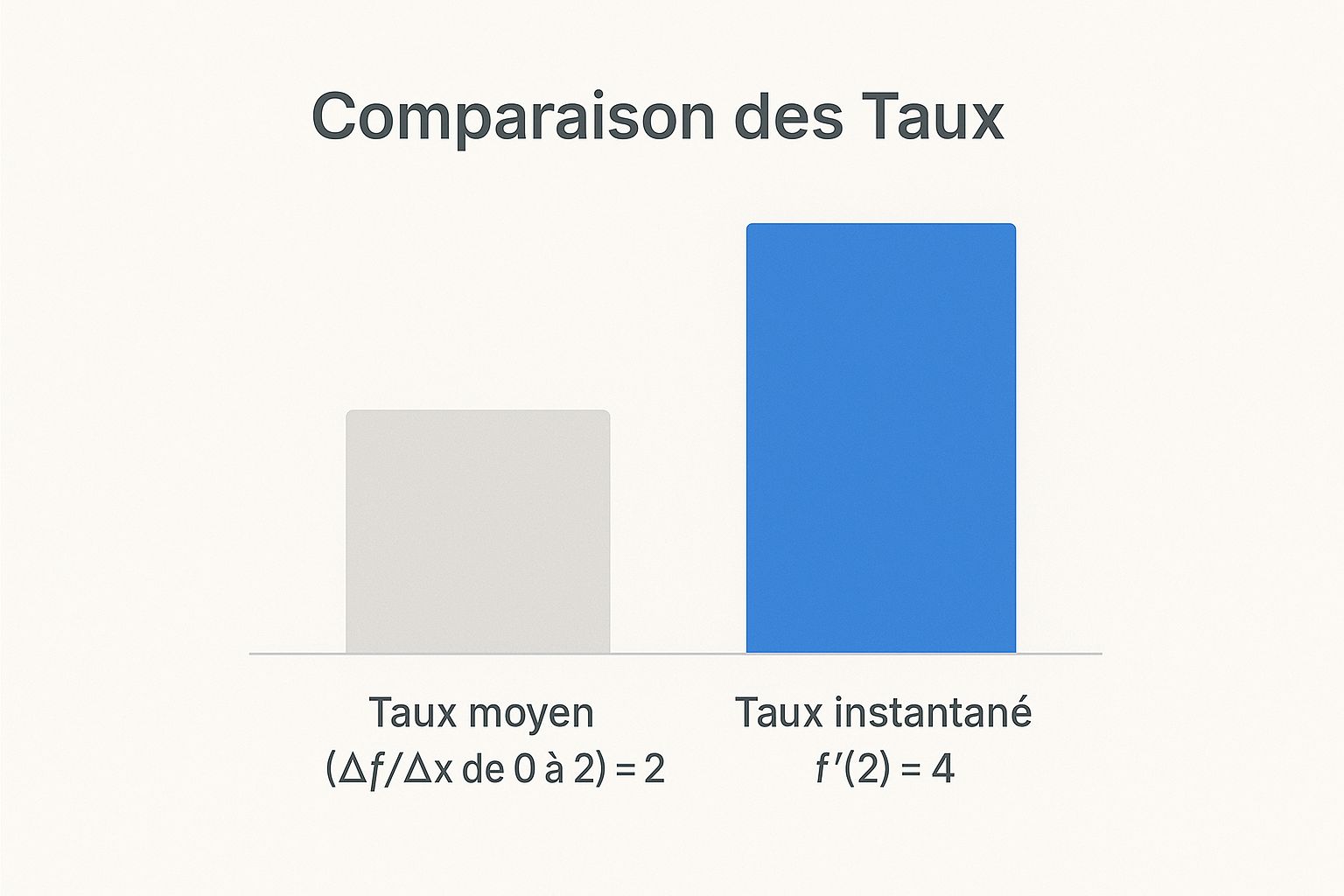
On voit bien que le taux instantané (la dérivée), qui est la pente exacte au point x=2, est beaucoup plus prononcé que le taux moyen calculé sur un intervalle plus grand.
Les règles de dérivation : vos raccourcis mathématiques
Calculer la dérivée en revenant toujours à la définition formelle avec les limites, c'est long et ça peut devenir pénible. Heureusement, il existe des règles qui agissent comme de puissants raccourcis pour dériver presque n'importe quelle fonction. Votre but, ce n'est pas de les apprendre par cœur sans réfléchir, mais de comprendre quand et comment les utiliser.
Voici les règles incontournables que vous verrez en calcul différentiel au Cégep :
- Règle de la puissance : La plus simple et la plus utilisée. Pour dériver xⁿ, on descend l'exposant en avant et on le diminue de 1. Par exemple, la dérivée de x³ devient 3x².
- Règle du produit : On l'utilise pour dériver une multiplication de deux fonctions, comme f(x)g(x). La formule, c'est (la dérivée de la première) × (la deuxième) + (la première) × (la dérivée de la deuxième).
- Règle du quotient : Essentielle quand on dérive une fraction, du type f(x)/g(x). La formule est un peu plus complexe, mais elle suit une logique qui ressemble à celle du produit.
- Règle en chaîne : C'est probablement la règle la plus puissante, mais c'est aussi celle qui demande le plus de pratique. Elle sert à dériver des fonctions qui sont « imbriquées » l'une dans l'autre, comme sin(x²). On dérive la fonction « extérieure », puis on multiplie par la dérivée de ce qui est à « l'intérieur ».
Maîtriser ces règles est un passage obligé. Une étude menée auprès de 500 étudiants en sciences au Collège Dawson a montré que 65 % d'entre eux avaient des difficultés au début, souvent à cause d'une compréhension fragile de l'algèbre et des limites. L'introduction de nouvelles approches pédagogiques a toutefois permis de faire grimper le taux de réussite de 68 % à 78 %. Pour en apprendre davantage, vous pouvez consulter les détails des cours de mathématiques de Dawson.
Exemple concret de dérivation
Prenons une fonction simple pour voir comment ça marche : f(x) = 5x³ + 2x. Pour la dériver, on va s'occuper de chaque morceau séparément en utilisant la règle de la puissance.
- Dériver 5x³ : L'exposant, c'est 3. On le multiplie par le coefficient 5, ce qui donne 15. Ensuite, on réduit l'exposant de 1, ce qui donne x². Le résultat est 15x².
- Dériver 2x : C'est la même chose que 2x¹. L'exposant est 1. On multiplie 2 par 1, ce qui donne 2. On réduit l'exposant de 1, ce qui donne x⁰, et on sait que n'importe quoi à la puissance 0 vaut 1. Le résultat est donc 2.
La dérivée de la fonction au complet, qu'on note f'(x), est simplement la somme de ces deux résultats : f'(x) = 15x² + 2.
Cette nouvelle fonction, f'(x), est super pratique. Si on veut connaître la pente de la courbe de notre fonction de départ au point x = 1, il suffit de calculer f'(1). Ça nous donne 15(1)² + 2 = 17. La pente à cet endroit est de 17.
La clé, c'est vraiment la pratique. Plus vous ferez d'exercices, plus l'application de ces règles deviendra un réflexe. L'objectif, c'est de regarder une fonction et de savoir presque instantanément quelle(s) règle(s) utiliser pour la décomposer et la dériver sans hésiter.
Appliquer le calcul différentiel à des problèmes réels
Après avoir jonglé avec les limites et les dérivées, une question brûle les lèvres : à quoi ça sert, concrètement? Le calcul différentiel au Cégep n'est pas qu'un simple exercice de style pour matheux. C'est une véritable boîte à outils qui permet de décortiquer et de résoudre une foule de problèmes du monde réel.
C'est ici que la magie opère et que les concepts abstraits prennent enfin vie. Vous allez voir comment l'idée toute simple de la pente d'une tangente peut aider une entreprise à maximiser ses profits, un ingénieur à concevoir une structure plus solide, ou un physicien à prédire le mouvement d'un projectile.
On va se concentrer sur trois applications incontournables de votre parcours : les problèmes d’optimisation, l'analyse de fonctions et les fameux taux liés. Chacune de ces applications transforme la théorie en une compétence pratique et vraiment utile.
Trouver le meilleur scénario avec l’optimisation
L'optimisation, c'est sans doute l'une des applications les plus parlantes et puissantes de la dérivée. Le principe est d'une simplicité désarmante : on cherche à trouver le maximum ou le minimum d'une situation, en respectant certaines règles du jeu.
Pensez à une entreprise qui veut fabriquer une canette de boisson gazeuse. Son but? Utiliser le moins d'aluminium possible pour un volume fixe, disons 355 ml. Moins de métal, ça veut dire moins de coûts et plus de profits. C'est un problème d'optimisation pur et dur.
La bonne nouvelle, c'est qu'il existe une recette quasi infaillible pour y arriver. Tout repose sur une idée centrale : les sommets et les creux d'une courbe se trouvent toujours là où la pente est nulle, c'est-à-dire là où la dérivée est égale à zéro.
Voici la marche à suivre, étape par étape :
- Identifier les variables : Qu'est-ce qui peut changer? Dans notre exemple, ce sont le rayon et la hauteur de la canette.
- Définir la fonction à optimiser : Qu'est-ce qu'on veut rendre maximal ou minimal? Ici, c'est la surface totale de l'aluminium.
- Trouver la contrainte : Quelle est la condition qu'on ne peut pas changer? Le volume doit absolument être de 355 ml.
- Simplifier la fonction : On utilise la contrainte pour réécrire la fonction de surface avec une seule variable.
- Calculer la dérivée et trouver les points critiques : On dérive, on pose le résultat égal à zéro, et on isole la variable pour trouver les dimensions potentiellement optimales.
- Valider le résultat : On vérifie si on a bien trouvé un minimum (et non un maximum), souvent avec le test de la dérivée seconde.
Cette méthode est un vrai couteau suisse. Elle s'applique autant en économie pour maximiser un revenu qu'en ingénierie pour minimiser une perte d'énergie. Si ces problèmes vous semblent corsés, un soutien scolaire spécialisé en sciences peut vous aider à démystifier la logique derrière chaque étape.
Dessiner le portrait complet d'une fonction
L'analyse de fonction, c'est un peu l'épreuve finale du calcul différentiel au Cégep. L'objectif? Tracer le graphique le plus précis possible d'une fonction, sans avoir à calculer des milliers de points au hasard. Pour y arriver, la dérivée première et la dérivée seconde deviennent vos meilleurs alliés.
La dérivée première, f'(x), vous indique le sens de la marche.
- Si f'(x) > 0, la fonction est en train de monter (croissante).
- Si f'(x) < 0, la fonction est en train de descendre (décroissante).
- Si f'(x) = 0, vous êtes sur un sommet ou dans un creux.
La dérivée seconde, f''(x), vous informe sur la courbure du graphique, ce qu'on appelle la concavité.
- Si f''(x) > 0, la courbe est creusée vers le haut (comme un sourire ou un bol).
- Si f''(x) < 0, la courbe est tournée vers le bas (comme un froncement de sourcils ou un bol à l'envers).
- Si f''(x) = 0, vous avez peut-être trouvé un point d'inflexion, là où la courbure change de direction.
En combinant toutes ces informations, vous pouvez dessiner un portrait-robot incroyablement fidèle de la fonction. Vous révélez tous ses secrets : ses hauts, ses bas, ses changements de cap et sa forme générale. C'est comme obtenir la carte topographique complète de son comportement.
Comprendre les taux de variation liés
Les problèmes de taux liés sont souvent la bête noire des étudiants, mais ils sont aussi parmi les plus intéressants. Ils permettent de comprendre comment la vitesse de changement d'une chose influence la vitesse de changement d'une autre.
L'exemple classique, c'est celui de l'échelle appuyée contre un mur. Si le bas de l'échelle glisse et s'éloigne du mur à une certaine vitesse, à quelle vitesse le haut de l'échelle descend-il?
La clé pour résoudre ces énigmes est la dérivation implicite par rapport au temps. On commence par trouver une relation géométrique (souvent le théorème de Pythagore) qui lie les variables. Ensuite, on dérive chaque morceau de l'équation par rapport au temps (t). Cela fait apparaître comme par magie les taux de variation (les fameux dx/dt et dy/dt) qu'on cherche à trouver.
Cette compétence est cruciale en physique et en génie pour analyser des systèmes où tout bouge en même temps. En maîtrisant ces applications, le calcul différentiel passe du statut de matière abstraite à celui d'outil d'analyse puissant, un atout indispensable pour la suite de votre parcours.
Maîtriser les théorèmes clés du calcul
Pour vraiment réussir en calcul différentiel au Cégep, il ne suffit pas de mémoriser des formules. Le secret, c’est de comprendre les grandes « règles du jeu » qui expliquent pourquoi tout ça fonctionne. On va explorer ensemble les théorèmes qui sont la véritable colonne vertébrale du calcul, mais sans le jargon compliqué.
Loin d'être de la théorie abstraite pour les profs, ces théorèmes sont les gardiens de la logique. Ils nous donnent des certitudes sur le comportement des fonctions, une étape essentielle avant de plonger dans des problèmes plus complexes.
Le théorème des accroissements finis : une garantie de vitesse
Le théorème des accroissements finis est l'un des plus puissants, mais aussi des plus faciles à visualiser. Imaginez que vous faites un trajet en voiture de 120 km en exactement deux heures. Simple calcul, votre vitesse moyenne est de 60 km/h.
Ce que ce théorème garantit est tout simple : à au moins un moment durant votre voyage, votre compteur de vitesse a affiché exactement 60 km/h. Vous avez peut-être accéléré ou ralenti, mais il y a eu au moins un instant précis où votre vitesse instantanée (la dérivée) a égalé votre vitesse moyenne. C’est une certitude.
Graphiquement, ça veut dire que pour n'importe quelle courbe lisse entre deux points, il existe au moins un endroit où la pente de la tangente est parfaitement identique à la pente de la ligne droite qui relie le point de départ au point d'arrivée.
Ce principe est fondamental. Il est à la base de nombreuses démonstrations et nous prouve qu'on peut faire confiance aux dérivées pour analyser une fonction dans son ensemble.
Le théorème de Rolle : un cas particulier très utile
Le théorème de Rolle est en fait une version spécifique du théorème des accroissements finis. Il s'applique quand une fonction commence et finit son parcours exactement à la même hauteur.
Pensez à une balle que vous lancez en l'air et que vous rattrapez à la même hauteur. Le théorème de Rolle nous confirme qu'au sommet de sa trajectoire, il y a eu un instant où sa vitesse verticale était nulle. C'est logique, non? Pour commencer à redescendre, la balle a bien dû arrêter de monter.
C'est exactement ce que dit le théorème :
- Si f(a) = f(b), alors il existe au moins un point c entre a et b.
- À ce point, la dérivée est zéro : f'(c) = 0.
- Ce point correspond à un sommet ou un creux, là où la tangente est parfaitement à l'horizontale.
La règle de l'Hôpital : la solution pour les limites difficiles
Parfois, en calculant une limite, on se heurte à des formes frustrantes comme 0/0 ou ∞/∞, qu'on appelle des formes indéterminées. La règle de l'Hôpital est l'outil parfait pour sortir de cette impasse.
Elle nous dit que si la limite du ratio de deux fonctions f(x)/g(x) donne une de ces formes, on peut simplement dériver le haut et le bas séparément, puis réessayer de calculer la limite. La plupart du temps, cette nouvelle limite est beaucoup plus simple à trouver. C'est une technique à garder précieusement dans sa boîte à outils pour les examens.
Le programme de calcul différentiel au Cégep, avec ses théorèmes et ses méthodes, s'est solidifié depuis les années 1970. Déjà en 1972, la majorité des cégeps offraient un cours de 75 heures. Dans les années 80, le taux de réussite en sciences tournait autour de 70 %, une statistique qui est demeurée stable grâce à des efforts pédagogiques constants. Pour en savoir plus sur l'évolution de ces cours, vous pouvez explorer les programmes de mathématiques universitaires.
Comprendre ces théorèmes peut demander un petit coup de pouce. Si vous trouvez ces concepts abstraits, discuter avec des tuteurs qualifiés peut vous aider à mieux visualiser ces règles et à les maîtriser pour de bon.
Des questions? On a les réponses.
Le calcul différentiel au Cégep peut sembler intimidant et c'est tout à fait normal d'avoir des questions. Cette section est là pour démystifier le sujet et vous donner des pistes de solution concrètes pour aborder la matière avec plus de confiance.
Quelles sont les erreurs les plus communes à éviter en calcul?
L'une des plus grosses erreurs, et de loin, c'est de négliger les bases. Le calcul différentiel est construit sur l'algèbre. Si vous n'êtes pas à l'aise avec la factorisation, la simplification d'expressions ou la résolution d'équations, c'est un peu comme vouloir construire un gratte-ciel sur des fondations en sable. Ça ne tiendra pas longtemps.
Un autre piège classique est de mélanger la valeur d'une fonction en un point précis, soit f(c), et sa limite quand x s'approche de ce point. La limite, c'est le comportement de la fonction autour du point, pas nécessairement sa valeur exacte sur le point. C'est une nuance cruciale qui est à la base de toute la matière.
Finalement, la gestion du temps pendant un examen est souvent ce qui fait la différence. Sous la pression, il est facile de se précipiter et de faire des erreurs d'inattention, comme oublier un signe négatif ou appliquer la mauvaise règle de dérivation.
Le meilleur moyen d'éviter ces pièges? Soyez proactif. Prenez le temps chaque semaine de rafraîchir vos notions d'algèbre. Pour vous assurer d'avoir bien compris un nouveau concept, essayez de l'expliquer à un ami. Si vos explications ne sont pas claires, c'est le signe qu'il faut y revenir.
Comment se préparer efficacement pour les examens?
Oubliez le bachotage de dernière minute. La clé du succès en calcul différentiel, c'est la régularité. Mieux vaut faire quelques exercices chaque jour que de s'enfermer pendant 8 heures la veille d'un examen. C'est en pratiquant constamment que les concepts s'ancrent réellement.
Considérez les anciens examens comme vos meilleurs alliés. Ne faites pas que les résoudre; analysez chacune de vos erreurs. Était-ce une simple faute de calcul? Une mauvaise compréhension d'un théorème? Une règle que vous aviez oubliée? Identifier la source de vos erreurs est la seule façon de ne pas les répéter.
Former un groupe d'étude peut aussi changer la donne. Expliquer un concept à quelqu'un d'autre est l'une des techniques d'apprentissage les plus puissantes. Et parfois, un camarade aura une façon d'expliquer un point qui vous semblait obscur, et tout deviendra clair.
Voici une petite routine qui a fait ses preuves :
- Pratique quotidienne : Visez 3 à 5 exercices par jour. Juste assez pour que la matière reste fraîche.
- Simulation d'examen : Une semaine avant le jour J, faites un vieil examen dans les conditions réelles (temps limité, sans aide).
- Journal d'erreurs : Notez vos erreurs récurrentes. Elles vous indiquent exactement sur quoi concentrer vos efforts.
- Enseignement mutuel : Organisez une séance avec votre groupe pour décortiquer les problèmes les plus coriaces.
Où trouver les meilleures ressources pour obtenir de l'aide?
Personne ne s'attend à ce que vous affrontiez ce défi seul. La première ressource, la plus évidente, est votre professeur. Ses heures de disponibilité sont une occasion en or de poser des questions précises. N'hésitez jamais à les utiliser.
La plupart des cégeps ont aussi des centres d'aide en mathématiques, souvent animés par des tuteurs ou d'autres professeurs. C'est gratuit et incroyablement utile pour débloquer un problème ponctuel.
Bien sûr, il y a une tonne de ressources en ligne. Des plateformes comme Allô Prof ou Khan Academy sont excellentes pour revoir une notion avec une vidéo. Par contre, si vous avez besoin d'un soutien plus constant et personnalisé, le tutorat et l'aide aux devoirs en ligne peuvent s'adapter à votre rythme et cibler directement vos faiblesses.
Le plus important : n'attendez pas d'être complètement perdu. Dès qu'un concept vous semble flou, allez chercher de l'aide. Le calcul est cumulatif, et une petite incompréhension aujourd'hui peut devenir un énorme blocage demain.
Le calcul différentiel est-il vraiment utile pour mon avenir?
La réponse est un oui retentissant. Considérer ce cours comme une simple étape obligée est une vision à court terme. Le calcul différentiel au Cégep est bien plus qu'une matière; c'est l'apprentissage d'une nouvelle façon de penser. La rigueur, la logique et la capacité à modéliser des phénomènes en changement sont des compétences qui vous suivront partout.
- En ingénierie, c'est la base pour tout, de la conception d'un pont à l'analyse d'un circuit électrique.
- En économie, des concepts comme le coût marginal ou le revenu marginal, essentiels à la prise de décision, découlent directement de la dérivée.
- En informatique, l'intelligence artificielle et l'apprentissage automatique reposent sur des principes de calcul, notamment pour optimiser les algorithmes.
- En physique, c'est simple : pas de calcul, pas de description du mouvement, de la vitesse ou de l'accélération.
Ce cours n'est donc pas qu'un prérequis, c'est un véritable investissement dans votre coffre à outils intellectuel et professionnel.


