Pour calculer le volume d'un cylindre, il y a une formule incontournable à maîtriser : V = πr²h. Cette simple équation permet de déterminer l'espace qu'occupe n'importe quel objet de forme cylindrique. C'est une compétence de base en géométrie, mais qui se révèle étonnamment pratique dans plein de situations du quotidien.
Comprendre la formule du volume d'un cylindre
Plongeons un peu dans cette formule pour voir ce qu'elle cache. Chaque symbole a un rôle bien précis et, une fois qu'on a saisi la fonction de chacun, le calcul devient beaucoup plus intuitif.

Pour bien visualiser le concept, imaginez que vous empilez des pièces de monnaie, l'une sur l'autre. L'aire d'une seule pièce (un disque) se calcule avec la formule πr², où 'r' est le rayon. Si vous continuez à empiler ces pièces jusqu'à atteindre une hauteur 'h', vous obtenez le volume total du cylindre. C'est aussi simple que ça!
Les composantes de la formule expliquées
La formule V = πr²h peut sembler un peu intimidante au premier abord, mais elle ne combine en réalité que trois éléments simples :
- V représente le Volume, c'est-à-dire l'espace que l'on cherche à mesurer.
- π (pi) est une constante mathématique célèbre. Sa valeur est d'environ 3,14159. C'est un nombre essentiel dès qu'on travaille avec des cercles.
- r est le rayon de la base circulaire du cylindre.
- h désigne la hauteur du cylindre, c'est-à-dire la distance entre les deux bases.
Voici un petit tableau récapitulatif pour y voir plus clair.
Les composantes de la formule du volume
Un résumé des variables nécessaires pour le calcul du volume d'un cylindre.
| Symbole | Signification | Rôle dans le calcul |
|---|---|---|
| V | Volume | Le résultat final que l'on cherche à obtenir. |
| π | Pi (≈ 3,14159) | Une constante qui relie la circonférence d'un cercle à son diamètre. |
| r | Rayon | Détermine la taille de la base circulaire. Doit être mis au carré. |
| h | Hauteur | Détermine la "longueur" du cylindre. |
En résumé, chaque partie de la formule a un rôle bien défini pour arriver au résultat final.
L'astuce, c'est de voir le volume comme la surface de la base qui est "étirée" sur toute la hauteur. Une fois que vous avez l'aire du cercle de base (πr²), il ne reste plus qu'à multiplier par la hauteur. Pour en savoir plus, n'hésitez pas à consulter notre guide complet sur les différentes méthodes pour calculer le volume d’un cylindre.
Cette notion est fondamentale dans des domaines comme l'ingénierie et l'architecture au Canada. Prenez un réservoir d'eau de 2 mètres de rayon et de 5 mètres de hauteur. Son volume serait : V = 3,14159 × 2² × 5, ce qui nous donne 62,83 mètres cubes.
Fait intéressant : en Ontario, où l'on construit plus de 1500 réservoirs de ce type chaque année, 68 % des structures de stockage sont cylindriques. Pourquoi? Simplement parce que cette forme permet d'optimiser l'espace de stockage tout en utilisant un minimum de matériaux. C'est l'efficacité à son meilleur!
Avec cette compréhension de base, l'application de la formule dans des exemples concrets devient tout de suite beaucoup plus facile.
Mettre la formule en application
Maintenant qu'on a vu la formule V = πr²h, passons à la pratique. Pour réussir son calcul de volume de cylindre, tout se joue sur deux points : avoir des mesures précises et bien respecter l’ordre des opérations. Une petite erreur au début, et c'est tout le résultat final qui est faussé.
La première chose à faire, c’est d’obtenir les bonnes mesures. Souvent, il est plus simple de mesurer le diamètre (la largeur complète du cercle) que le rayon lui-même. Il suffit de se rappeler que le rayon (r) est toujours la moitié du diamètre. Par exemple, si votre piscine hors terre fait 4 mètres de large, son rayon est de 2 mètres.
Ensuite, on mesure la hauteur (h) du cylindre. Prenez bien soin de mesurer droit, de la base jusqu'au sommet, pour ne pas fausser la donnée.
L'ordre des opérations à suivre
Une fois que vous avez vos mesures, l'ordre de calcul est vraiment important pour ne pas se tromper. Il faut toujours commencer par mettre le rayon au carré avant de faire les autres multiplications.
Voici la séquence à respecter :
- Mettre le rayon au carré (r²) : Multipliez le rayon par lui-même.
- Multiplier par Pi (π) : Prenez la valeur de π sur votre calculatrice (elle est souvent plus précise que 3,14) et multipliez-la par le résultat que vous venez d'obtenir.
- Multiplier par la hauteur (h) : Finalement, multipliez ce nouveau chiffre par la hauteur. Vous avez maintenant le volume!
Cette infographie vous montre le processus de façon simple et visuelle.
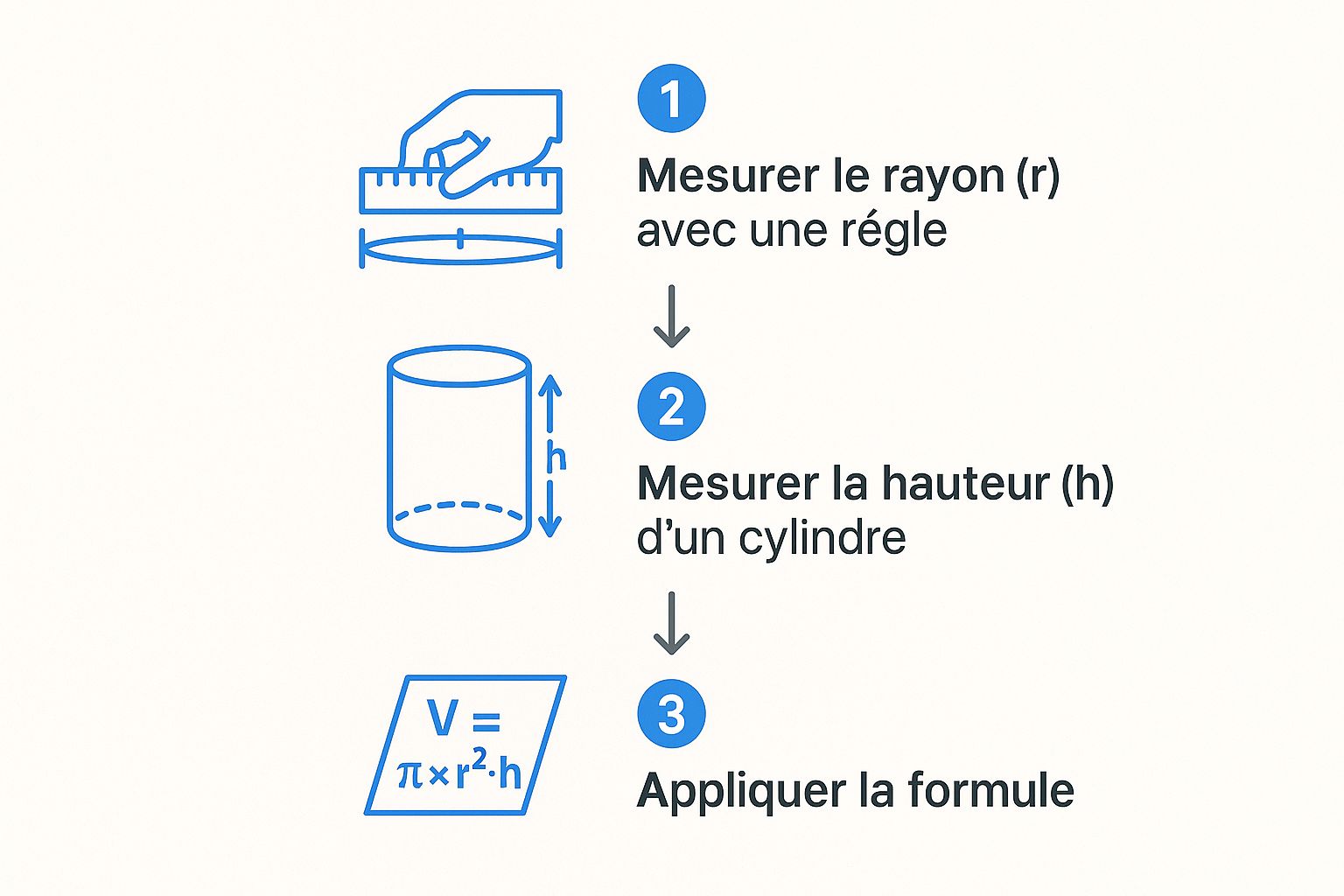
Comme vous le voyez, ça se résume à trois gestes clairs : mesurer le rayon, mesurer la hauteur, puis appliquer la formule en suivant bien les étapes.
Exemple concret avec une piscine
Imaginons que vous vouliez savoir combien d'eau mettre dans votre piscine cylindrique. Son diamètre est de 4 mètres et vous voulez une hauteur d'eau de 1,2 mètre.
- Le rayon (r), c'est la moitié du diamètre : 4 m / 2 = 2 m.
- Le rayon au carré (r²) est donc : 2 m × 2 m = 4 m².
- On multiplie par Pi : 4 m² × 3,14159 ≈ 12,57 m².
- On finit en multipliant par la hauteur (h) : 12,57 m² × 1,2 m = 15,08 m³.
Le volume d'eau nécessaire est donc d'environ 15,08 mètres cubes.
Maîtriser cette méthode, c'est un peu comme apprendre une recette de cuisine : si on suit bien l'ordre des étapes, le résultat est garanti. Une bonne méthode est la clé du succès.
Cette approche logique est d'ailleurs une compétence qui sert partout. Si vous cherchez des trucs pour mieux vous organiser dans vos études, jetez un œil à nos conseils sur comment étudier efficacement. En mathématiques comme dans le reste, une bonne méthode fait toute la différence.
Le calcul du volume dans des situations du quotidien
Le calcul du volume d’un cylindre n’est pas qu’un simple exercice scolaire; c’est une compétence pratique qui s’invite dans une foule de situations bien réelles. Savoir comment l'appliquer peut vous faire économiser du temps, de l'argent et vous éviter bien des maux de tête, que vous soyez en train de jardiner, de cuisiner ou même en pleins travaux de rénovation.

Pensez à votre jardin, par exemple. Vous venez de vous procurer une nouvelle jardinière cylindrique et vous devez savoir quelle quantité de terreau acheter. Si vous estimez mal la quantité, vous risquez de multiplier les allers-retours à la pépinière. C’est précisément ici que la formule V = πr²h devient votre meilleure alliée.
Estimer la terre pour une jardinière
Imaginons que votre nouvelle jardinière mesure 40 cm de diamètre et a une hauteur de 50 cm. Comment s’y prendre?
- On commence par trouver le rayon (r), qui est la moitié du diamètre : 40 cm / 2 = 20 cm.
- Ensuite, on calcule l'aire de la base (πr²) : π × (20 cm)² ≈ 3,14159 × 400 cm² ≈ 1256,64 cm².
- Finalement, on multiplie cette aire par la hauteur (h) : 1256,64 cm² × 50 cm = 62 832 cm³.
Ce résultat en centimètres cubes n'est pas très pratique. Heureusement, la conversion est simple : sachant que 1000 cm³ équivalent à 1 litre, on divise notre résultat par 1000. On obtient donc 62,8 litres. Vous savez maintenant qu’un sac de 60 litres de terreau ne sera pas tout à fait suffisant.
Savoir calculer le volume vous donne une autonomie précieuse. Cela transforme une simple estimation en une donnée précise, applicable à une multitude de projets, du calcul de la quantité de peinture pour un poteau à la capacité d'une cuve de récupération d'eau.
Calculer la capacité d'une casserole
Même en cuisine, cette formule se révèle étonnamment utile. Vous suivez une recette qui demande de faire mijoter 4 litres de soupe et vous vous demandez si votre plus grande casserole fera l’affaire.
Mesurons-la : elle a un diamètre de 24 cm et une hauteur de 14 cm.
- Le rayon (r) est donc de : 24 cm / 2 = 12 cm.
- Le volume (V) se calcule ainsi : π × (12 cm)² × 14 cm ≈ 3,14159 × 144 cm² × 14 cm ≈ 6333,4 cm³.
En convertissant en litres, on obtient environ 6,3 litres. Votre casserole est donc largement assez grande pour votre recette de 4 litres. Fini le stress du débordement!
Ces exemples montrent bien que le volume est une mesure clé, mais ce n'est pas toujours la seule à considérer. Pour des objets comme des tuyaux ou des rouleaux, il est aussi pertinent de connaître la surface extérieure. Pour approfondir ce sujet, n'hésitez pas à consulter notre article qui explique en détail comment calculer l'aire d'un cylindre.
Gérez bien les unités de mesure pour un résultat précis
L’une des erreurs les plus fréquentes dans le calcul du volume d’un cylindre ne vient pas de la formule elle-même, mais d’une simple distraction : le mélange des unités de mesure. C'est un piège classique qui peut fausser complètement votre résultat, même si votre raisonnement est parfait.

La règle d’or est simple. Avant de faire le moindre calcul, assurez-vous que toutes vos mesures (rayon, hauteur) sont exprimées dans la même unité. Si le rayon est en centimètres, la hauteur doit l'être aussi. Si vous mesurez une grande cuve en mètres, toutes les dimensions doivent être en mètres. C'est non négociable.
La cohérence des unités, une étape cruciale
Imaginons que vous devez calculer le volume d’un tuyau avec un rayon de 50 millimètres et une longueur de 2 mètres. Si vous multipliez ces chiffres tels quels, le résultat n'aura aucun sens. La bonne approche est de tout convertir dans une seule et même unité avant de commencer.
Vous pourriez, par exemple, tout ramener en millimètres :
- Rayon (r) : 50 mm
- Hauteur (h) : 2 mètres = 2000 mm
Ou, à l'inverse, tout passer en mètres :
- Rayon (r) : 50 millimètres = 0,05 m
- Hauteur (h) : 2 m
Le choix de l'unité dépend souvent du contexte et de ce qui vous semble le plus simple. L'important, c’est de ne jamais mélanger les deux. Pour vous aider à jongler avec ces conversions, n'hésitez pas à consulter des ressources fiables. Vous pouvez d’ailleurs explorer notre guide sur la conversion de mesures pour vous familiariser avec ces manipulations essentielles.
Un calcul juste commence toujours par des données cohérentes. Prenez ce réflexe de vérifier et de convertir vos unités avant même de toucher à la calculatrice. C'est une habitude qui vous évitera bien des erreurs, en maths comme en sciences.
Pensez à convertir le volume final
Une fois le calcul terminé, il reste souvent une dernière étape : rendre le résultat plus parlant. Par exemple, un volume en centimètres cubes (cm³) est rarement utilisé dans la vie de tous les jours. Il est beaucoup plus pratique de le convertir en litres pour se faire une idée concrète.
Voici quelques conversions clés à mémoriser pour y arriver :
Tableau de conversion des unités courantes
Pour convertir les unités de longueur et de volume et ainsi garantir des calculs précis, ce tableau est un excellent aide-mémoire.
| Unité initiale | Conversion | Unité finale | Exemple |
|---|---|---|---|
| centimètres cubes (cm³) | Diviser par 1000 | litres (L) | 50 000 cm³ = 50 L |
| mètres cubes (m³) | Multiplier par 1000 | litres (L) | 1 m³ = 1000 L |
Grâce à ces équivalences, si vous calculez que votre aquarium cylindrique a un volume de 50 000 cm³, vous saurez immédiatement qu'il vous faudra 50 litres d'eau pour le remplir. Cette étape finale rend votre résultat concret et applicable à des situations bien réelles.
Mettez vos connaissances à l'épreuve avec des exercices
Rien de tel que la pratique pour vraiment maîtriser une nouvelle notion. Maintenant que la formule du volume d'un cylindre n'a plus de secrets pour vous, il est temps de voir ce que vous avez dans le ventre avec quelques défis concrets. Ces exercices sont pensés pour vous pousser un peu plus loin que les exemples de base.
On va commencer en douceur avec un problème assez direct pour s'échauffer, puis on augmentera la difficulté d'un cran. Le but, ce n'est pas juste de trouver la bonne réponse, mais de solidifier votre raisonnement et de vous donner confiance.
Exercice 1 : La cannette de boisson gazeuse
C'est un grand classique, mais c'est parfait pour commencer. Une cannette de format standard mesure 12,2 cm de hauteur et a un diamètre de 6,6 cm. Quel est son volume en centimètres cubes (cm³), puis en millilitres (ml) ? Petit rappel : 1 cm³ équivaut à 1 ml.
- Les données du problème
- Hauteur (h) = 12,2 cm
- Diamètre = 6,6 cm (ce qui nous donne un rayon (r) de 3,3 cm)
- Votre mission
- Utiliser la fameuse formule V = πr²h pour trouver le volume.
- Donner le résultat en cm³ avant de le convertir en ml.
Ce premier exercice est idéal pour valider que vous êtes à l'aise avec l'application directe de la formule.
Exercice 2 : Le réservoir d'eau de pluie
Passons maintenant à un scénario un peu plus corsé qui demande de jouer un peu avec la formule. Imaginez un grand réservoir cylindrique pouvant contenir exactement 5000 litres d'eau. Vous savez que son rayon est de 0,8 mètre. Quelle est donc la hauteur de ce réservoir ?
Cette fois, on vous donne le volume, mais c'est la hauteur qui manque à l'appel. C'est un excellent exercice pour s'habituer à isoler une variable dans une équation.
L'astuce ici est de réarranger la formule V = πr²h pour trouver h. En divisant simplement les deux côtés par πr², on obtient la formule pour la hauteur : h = V / (πr²). N'oubliez pas de convertir les litres en mètres cubes pour que tout fonctionne (1000 litres = 1 m³).
Exercice 3 : Le tuyau en acier
Voilà un défi qui demande un peu plus de jus de cerveau. Vous devez calculer le volume d'acier nécessaire pour fabriquer un tuyau de 3 mètres de long. Le diamètre extérieur du tuyau est de 20 cm et son épaisseur est de 1 cm.
Pour y arriver, il faut voir le tuyau comme un cylindre creux. La méthode se décompose comme suit :
- Calculez le volume du grand cylindre (l'extérieur).
- Calculez le volume du "trou" à l'intérieur (le cylindre vide).
- Soustraire le volume intérieur du volume extérieur. Le résultat est le volume de métal utilisé.
C'est typiquement le genre de problème qui teste vraiment votre compréhension de la géométrie des volumes. Si vous trouvez ces défis stimulants mais que certains concepts vous donnent encore du fil à retordre, un accompagnement personnalisé peut tout changer. Pour aller plus loin et solidifier vos acquis, le tutorat en maths est une ressource fantastique pour obtenir des explications claires, à votre rythme.
Chez Centrétudes, nous sommes convaincus que la pratique est la clé du succès. Nos tuteurs certifiés sont là pour vous aider à transformer les défis mathématiques en réussites. Découvrez comment nous pouvons vous accompagner sur https://centretudes.ca.


