Le calcul de la pente se résume à une formule étonnamment simple : on divise la variation verticale (la « montée ») par la variation horizontale (la « course ») entre deux points. Cette formule, m = (y2 – y1) / (x2 – x1), est l'outil de base pour mesurer l'inclinaison d'une ligne, que ce soit sur un graphique ou dans une situation bien réelle.
Comprendre le calcul de la pente au quotidien
La notion de pente peut sembler tout droit sortie d'un cours de maths, mais elle est en fait partout autour de nous. C'est un concept qu'on évalue intuitivement chaque jour.
On y pense en grimpant une côte à vélo, en regardant un avion décoller ou même en analysant un graphique de ventes. Savoir comment la calculer, c'est simplement mettre un chiffre précis sur cette inclinaison.
Le calcul de la pente est essentiel dans une foule de domaines pratiques :
- Construction et génie civil : Pour s'assurer que l'eau s'écoule bien dans les tuyaux ou pour construire des routes et des rampes d'accès sécuritaires.
- Architecture : Pour concevoir des toits avec la bonne inclinaison, afin d'éviter que la pluie ou la neige ne s'accumule.
- Finance : Pour analyser la tendance d'une action en bourse; une pente positive, c'est un signe de croissance!
- Géographie : Pour décrire le relief d'un terrain et créer des cartes topographiques précises.
Les deux composantes clés de la pente
Pour calculer la pente, il faut juste maîtriser deux idées très simples : la variation verticale et la variation horizontale.
La variation verticale, qu'on appelle souvent la « montée » (rise en anglais), représente le changement de hauteur entre deux points. C'est la distance qu'on monte ou qu'on descend. Dans la formule, ça correspond à (y2 – y1).
La variation horizontale, ou la « course » (run en anglais), c'est le déplacement à l'horizontale entre ces deux mêmes points. Dans la formule, c'est (x2 – x1).
En résumé, la pente, c'est tout simplement le rapport entre la montée et la course. Une pente de 2, par exemple, veut dire que pour chaque pas que vous faites à l'horizontale, vous montez de deux pas à la verticale. C'est une mesure directe de l'inclinaison.
Imaginons que vous partez du point (2, 3) et que vous arrivez au point (4, 7). La montée est de 7 – 3 = 4 et la course est de 4 – 2 = 2. La pente est donc de 4 / 2 = 2. C'est aussi simple que ça!
La formule de la pente en un coup d'œil
Pour visualiser encore plus clairement, ce tableau décompose la formule de la pente pour une compréhension instantanée de chaque composant et de sa fonction.
| Symbole | Nom | Rôle dans la formule |
|---|---|---|
| m | Pente | C'est le résultat final, la valeur qui représente l'inclinaison de la droite. |
| (x1, y1) | Premier point | Les coordonnées du point de départ. |
| (x2, y2) | Deuxième point | Les coordonnées du point d'arrivée. |
| y2 – y1 | Variation verticale | Mesure le déplacement vertical (la montée ou la descente). |
| x2 – x1 | Variation horizontale | Mesure le déplacement horizontal (la course). |
Ce tableau aide à se souvenir que la pente n'est rien de plus qu'un ratio, une comparaison entre le déplacement vertical et horizontal.
Maîtriser ce calcul de base ouvre la porte à des analyses bien plus poussées et à une meilleure compréhension du monde qui nous entoure. Pour les élèves qui trouvent ce concept un peu difficile, un soutien ciblé peut vraiment faire toute la différence. Vous pouvez en apprendre davantage sur les approches pédagogiques en consultant les services de tutorat en mathématiques qui aident à solidifier ces notions fondamentales.
Maîtriser la formule de la pente avec des exemples
La fameuse formule de la pente, m = (y2 – y1) / (x2 – x1), est le cœur de tout calcul d'inclinaison. Pour vraiment la maîtriser, il ne suffit pas de l'apprendre par cœur; il faut la mettre en pratique, jongler avec les chiffres jusqu'à ce que sa logique devienne une seconde nature.
L'idée de base est simple : on mesure le rapport entre le déplacement vertical (« la montée ») et le déplacement horizontal (« l’avancée »). Peu importe que les chiffres soient positifs, négatifs ou même nuls, la formule s'applique toujours de la même façon.
Ce visuel illustre parfaitement le principe. On y décompose le calcul en ses deux composantes clés : la variation verticale, divisée par la variation horizontale.
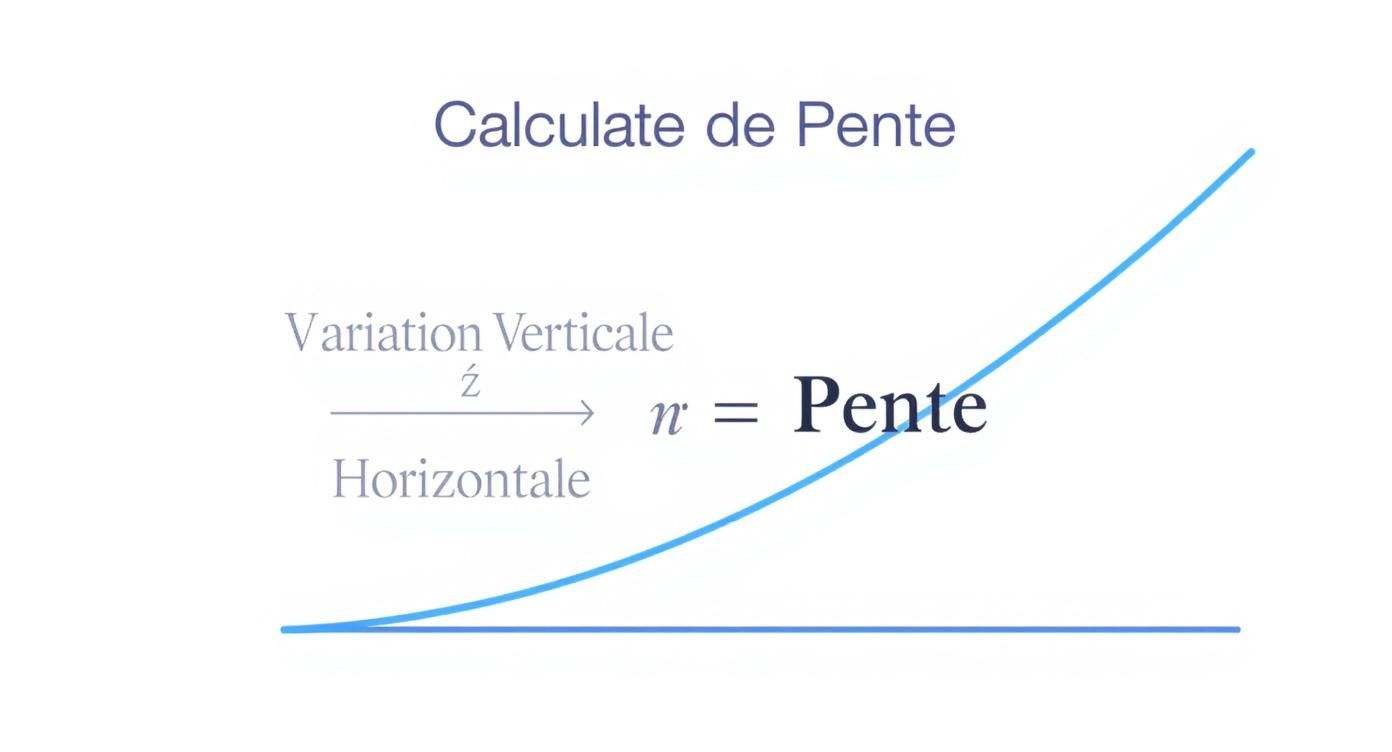
On voit bien qu'une pente positive, c'est tout simplement une ligne qui grimpe de gauche à droite, parce que la « montée » et « l'avancée » vont dans la même direction positive.
Application avec des coordonnées variées
Passons de la théorie à la pratique. Imaginons qu'on suive la trajectoire d'un drone. Il décolle d'un point A (-4, -2) pour atteindre un point B (2, 7). Pour trouver la pente de son vol, on doit d'abord identifier nos coordonnées :
- Point de départ (x1, y1) = (-4, -2)
- Point d'arrivée (x2, y2) = (2, 7)
Maintenant, appliquons la formule :
m = (7 – (-2)) / (2 – (-4))
m = (7 + 2) / (2 + 4)
m = 9 / 6 = 1,5
La pente est de 1,5. Concrètement, ça veut dire que pour chaque mètre que le drone parcourt à l'horizontale, il s'élève de 1,5 mètre. La pente est positive, ce qui confirme bien que le drone est en pleine ascension.
La plus grosse erreur à éviter, c'est de mélanger l'ordre des coordonnées. Si vous commencez par y2 pour le calcul vertical, vous devez absolument commencer par x2 pour le calcul horizontal. La cohérence, c'est la clé. (y2 – y1) / (x2 – x1) est correct, tout comme (y1 – y2) / (x1 – x2), mais un mélange des deux donnera un résultat complètement faux.
Un exemple avec une pente négative
Prenons un autre scénario : un sentier de randonnée qui descend. Vous partez d'un point en altitude C (1, 5) pour arriver à un point plus bas, D (6, -5).
- Point de départ (x1, y1) = (1, 5)
- Point d'arrivée (x2, y2) = (6, -5)
Le calcul de la pente donne ceci :
m = (-5 – 5) / (6 – 1)
m = -10 / 5 = -2
La pente est de -2. Le signe négatif nous confirme qu'il s'agit bien d'une descente. Pour chaque mètre parcouru à plat, le sentier descend de deux mètres. C'est une information cruciale, pas seulement pour les randonneurs, mais aussi pour les ingénieurs civils.
Ces exemples montrent bien à quel point la formule est polyvalente. Positifs ou négatifs, les chiffres ne changent rien au processus. Parfois, même avec des explications claires, les concepts mathématiques peuvent rester un défi. Si votre enfant éprouve des difficultés, un accompagnement personnalisé peut faire toute la différence. C'est pourquoi notre service de tutorat et d’aide aux devoirs en maths est conçu pour redonner confiance et consolider la compréhension.
Trouver la pente à partir de l'équation d'une droite
Parfois, pour calculer la pente, on n'a pas deux points sous la main, mais simplement une équation. Savoir extraire cette information cruciale directement de la formule est une compétence essentielle en algèbre. Ça simplifie énormément l'analyse des graphiques et la résolution de problèmes.
Heureusement, les équations de droites sont souvent écrites d'une manière qui nous facilite la tâche. Il suffit de savoir où regarder et comment lire la structure de l'équation.
Identifier la pente dans la forme y = mx + b
La façon la plus simple et la plus directe de lire une pente, c'est avec l'équation sous sa forme réduite, aussi appelée la forme pente-ordonnée à l'origine : y = mx + b.
Dans cette formule bien connue, chaque lettre a son rôle :
- y représente la coordonnée verticale.
- x représente la coordonnée horizontale.
- m est le coefficient directeur, autrement dit, la pente.
- b est l'ordonnée à l'origine, c'est-à-dire le point où la droite croise l'axe des y.
C'est aussi simple que ça : quand l'équation est sous cette forme, le nombre qui multiplie
xest directement la pente que vous cherchez. Aucun calcul n'est nécessaire.
Par exemple, si on vous donne l'équation y = 3x – 5, la pente (m) est tout simplement 3. Pour y = -0,5x + 2, la pente est -0,5. C'est un raccourci super pratique, surtout pendant les examens où chaque minute compte.
Pour les élèves qui veulent vraiment maîtriser cette compétence, particulièrement en vue des épreuves de fin d'année, il existe des ressources spécialisées. Vous pouvez en apprendre plus sur les stratégies gagnantes avec notre guide sur la préparation à l'examen du ministère de mathématiques SN de secondaire 4.
Extraire la pente de la forme générale Ax + By + C = 0
Toutes les équations ne sont pas présentées de manière aussi claire. On rencontre souvent la forme générale : Ax + By + C = 0.
À première vue, la pente n'est pas visible. L'astuce, c'est de manipuler un peu l'équation pour l'isoler et la ramener à la forme familière y = mx + b. Le but du jeu est de mettre y tout seul d'un côté du signe égal.
Prenons un exemple concret avec l'équation 6x + 2y – 8 = 0.
On commence par déplacer les termes en x et la constante de l'autre côté :2y = -6x + 8
Ensuite, on divise toute l'équation par le coefficient de y (ici, c'est 2) pour que y soit seul :y = (-6/2)x + (8/2)
Il ne reste plus qu'à simplifier :y = -3x + 4
Et voilà! L'équation est maintenant sous la forme y = mx + b. On voit tout de suite que la pente m est -3. Cette technique de réarrangement est une compétence de base pour analyser n'importe quelle équation de droite.
Traduire la pente en pourcentage et en degrés
Une valeur de pente brute, comme 0,75, peut paraître abstraite. Pourtant, quand on la convertit en pourcentage ou en degrés, elle prend un sens concret et devient immédiatement plus parlante, que ce soit pour un projet de construction ou pour analyser le dénivelé d'un sentier de randonnée.
Cette traduction est essentielle pour appliquer le calcul de la pente dans le monde réel. Par exemple, un panneau de signalisation routière n'indiquera jamais « pente de 0,12 ». Il affichera plutôt « 12 % », une convention universelle qui rend l'information accessible à tous.

Convertir la pente en pourcentage
Transformer la valeur numérique d’une pente en pourcentage est sans doute l'opération la plus simple et la plus fréquente. La formule est directe :
Pente (%) = Valeur de la pente × 100
Prenons un exemple concret. Vous construisez une rampe d'accès et votre calcul vous donne une pente de 0,08. Pour la traduire en pourcentage, il suffit de multiplier ce chiffre par 100.
0,08 × 100 = 8 %
Votre rampe a donc une inclinaison de 8 %. Cela veut dire que pour chaque 100 centimètres parcourus à l'horizontale, la rampe s'élève de 8 centimètres. Cette mesure est fondamentale pour respecter les normes d'accessibilité, par exemple.
Ce principe s'applique dans de nombreux domaines. En agriculture, la pente influence directement les techniques de culture et la productivité. Selon des données de l'Université de Californie à Davis, 28 % des terres agricoles de la région se situent sur des pentes variant entre 3 % et 8 %. Une pente de 10 %, représentant 10 mètres de dénivelé pour 100 mètres horizontaux, impose déjà des méthodes spécifiques pour contrer l'érosion du sol. Vous pouvez approfondir l'impact de la topographie en consultant cet article sur le calcul de pente entre deux points.
Un pourcentage de pente supérieur à 15 % est souvent considéré comme « fort » pour une route ou un sentier. Fait intéressant, une pente de 100 % correspond à un angle de 45°, où la montée verticale est égale à l'avancée horizontale.
Transformer la pente en degrés
Pour des applications plus techniques, comme en physique ou en ingénierie, il est souvent nécessaire de connaître l’angle précis de la pente en degrés. Cette conversion fait appel à une fonction trigonométrique bien connue : l'arc tangente (tan⁻¹).
La formule est la suivante :
Angle (en degrés) = tan⁻¹(Valeur de la pente)
Imaginons que vous deviez installer des panneaux solaires sur un toit dont la pente est de 0,47. Pour trouver l'angle d'inclinaison :
- Prenez votre calculatrice scientifique.
- Assurez-vous qu'elle est en mode « degrés » (DEG).
- Calculez l'arc tangente de 0,47 :
tan⁻¹(0,47).
Le résultat est approximativement 25,18°. L'inclinaison de votre toit est donc d'environ 25 degrés, une information cruciale pour optimiser l'exposition des panneaux au soleil. La trigonométrie, souvent étudiée en sciences, est un outil puissant pour ce genre de calculs. Pour les élèves qui souhaitent renforcer leurs compétences dans ce domaine, un service de tutorat en sciences peut offrir un soutien précieux pour maîtriser ces concepts.
Gérer les cas particuliers de pentes
Toutes les droites ne sont pas inclinées. Si la plupart des calculs de pente que vous ferez impliquent une montée ou une descente, deux cas particuliers se démarquent et sont essentiels à maîtriser : les droites parfaitement horizontales et celles qui sont parfaitement verticales.

Ces situations peuvent sembler être des exceptions, mais les comprendre vous donnera une vision complète et solide du concept de pente. On les retrouve plus souvent qu'on ne le pense, du plancher d'une maison jusqu'à un mur parfaitement droit.
Comprendre la pente nulle des droites horizontales
Imaginez-vous en train de marcher sur un sol parfaitement plat. Vous avancez, mais votre altitude ne change jamais. Voilà l'illustration parfaite d'une droite horizontale.
Pour calculer la pente entre deux points sur cette droite, disons (2, 5) et (8, 5), on reprend notre bonne vieille formule :
m = (y2 – y1) / (x2 – x1)
m = (5 – 5) / (8 – 2)
m = 0 / 6 = 0
Ici, la variation verticale (la « montée ») est complètement nulle. Et comme diviser zéro par n'importe quel autre nombre donne toujours zéro, la pente d'une droite horizontale est toujours égale à 0. C'est une règle mathématique simple, mais fondamentale à retenir.
Le cas de la pente indéfinie pour les droites verticales
Maintenant, visualisez un mur parfaitement vertical, comme celui d'une falaise. Pour ce type de droite, la situation s'inverse. C'est la coordonnée x qui ne change jamais, peu importe où l'on se trouve en hauteur.
Prenons deux points sur une telle droite, par exemple (3, 1) et (3, 9).
m = (y2 – y1) / (x2 – x1)
m = (9 – 1) / (3 – 3)
m = 8 / 0
On se heurte ici à une impossibilité mathématique : la fameuse division par zéro. Il est tout simplement impossible de définir le résultat de cette opération. C'est pourquoi la pente d'une droite verticale est qualifiée d'indéfinie ou de non définie. Ce n'est pas un nombre, mais un concept qui indique une inclinaison infinie, tout droit vers le haut.
Pour vous donner une idée concrète, en urbanisme, une pente de 20 % seulement suffit à augmenter les coûts de construction de 25 % et à accroître les risques de glissements de terrain. On est loin de l'infini!
Pour vous aider à visualiser rapidement ces concepts, voici un petit tableau récapitulatif.
| Comparatif des quatre types de pente | |||
|---|---|---|---|
| Type de Pente | Valeur de 'm' | Direction de la Droite | Exemple concret |
| Positive | m > 0 | Monte de gauche à droite | Une colline qui grimpe |
| Négative | m < 0 | Descend de gauche à droite | Une piste de ski en descente |
| Nulle | m = 0 | Horizontale | Un plancher plat |
| Indéfinie | Division par 0 | Verticale | Un mur parfaitement droit |
Ce tableau est un excellent aide-mémoire pour ne plus jamais confondre ces quatre situations.
Comprendre ces deux exceptions est crucial. Une pente nulle n'est pas l'absence de pente; c'est une pente parfaitement horizontale. Une pente indéfinie n'est pas une pente immense; c'est une ligne verticale, ce qui est mathématiquement très différent.
La maîtrise de ces notions est souvent évaluée lors des contrôles scolaires. Pour aider les élèves à solidifier ces bases, rien ne vaut des exercices ciblés. N'hésitez pas à consulter nos ressources pour la préparation aux examens ministériels de mathématiques de 6e année afin d'accéder à des outils pédagogiques adaptés.
On répond à vos questions sur le calcul de pente
Même avec les formules bien en tête, il reste souvent quelques petites zones d'ombre. C'est tout à fait normal! On a rassemblé ici les questions qui reviennent le plus souvent pour vous aider à y voir plus clair.
L'idée, c'est de vous donner des réponses directes et pratiques pour que le calcul de pente n'ait plus de secret pour vous.
Quelle est la différence entre une pente positive et négative?
C'est une excellente question, et la distinction est très visuelle. Une pente positive signifie que la droite « monte » quand on la regarde de gauche à droite. Autrement dit, si x augmente, y augmente aussi. Imaginez que vous gravissez une côte à vélo; c'est exactement ça, une pente positive.
À l'inverse, une pente négative, c'est une droite qui « descend ». Pendant que x avance, y diminue. Pensez cette fois à une descente en ski. Comprendre cette différence est essentiel pour bien interpréter n'importe quel graphique, que ce soit en maths ou pour analyser des données financières.
Peut-on calculer la pente avec un seul point?
La réponse courte est non, c'est mathématiquement impossible. La pente, par définition, mesure l'inclinaison entre deux points. Un point tout seul ne nous dit rien sur la direction d'une droite.
Pensez-y : une infinité de droites, chacune avec sa propre pente, peuvent passer par un seul et même point. Pour définir une pente unique, il vous faut absolument un deuxième point de référence, ou alors l'équation complète de la droite.
Dans quels domaines concrets utilise-t-on le calcul de pente?
Bien plus souvent qu'on ne le pense! Le calcul de pente est une compétence super pratique dans plein de métiers et même au quotidien. Par exemple :
- En ingénierie civile : Pour dessiner des routes sécuritaires ou concevoir des systèmes de drainage où l'eau doit s'écouler naturellement.
- En architecture : Pour calculer l'angle parfait d'un toit afin que la pluie et la neige s'évacuent correctement.
- En finance : Pour analyser si la valeur d'une action ou d'un indice boursier est sur une tendance à la hausse ou à la baisse.
- En géographie : Pour lire des cartes topographiques et évaluer la difficulté d'un sentier de randonnée.
Est-ce que l'unité de mesure de x et y est importante?
Oui, c'est un détail crucial! Pour que votre calcul de pente ait du sens, les unités des axes x (horizontal) et y (vertical) doivent être les mêmes.
Si vous mesurez une élévation en mètres sur une distance en kilomètres, vous devez absolument tout convertir dans la même unité avant d'appliquer la formule. Par exemple, transformez les kilomètres en mètres. Si vous oubliez cette étape, le résultat sera complètement faussé et votre pente, incorrecte.
Chez Centrétudes, nous savons que la confiance en mathématiques se bâtit sur des bases solides. Si votre enfant a besoin d'un coup de pouce pour transformer ses questions en certitudes, nos tuteurs certifiés sont là pour l'accompagner. Découvrez nos services de tutorat personnalisé sur centretudes.ca.


