Pour faire simple, calculer une pente, c’est mesurer à quel point ça monte (ou ça descend) verticalement par rapport à la distance qu’on parcourt à l’horizontale. Il s’agit simplement d'un rapport entre la « montée » et la « course », mais c'est une idée qu'on retrouve bien au-delà des salles de classe.
Comprendre la pente au-delà des mathématiques

La pente n'est pas juste un concept abstrait coincé dans un manuel de géométrie. C'est une mesure très concrète de l'inclinaison que nous croisons tous les jours, souvent sans même y porter attention.
Pensez à la rampe que vous grimpez à vélo, à l'inclinaison du toit de votre maison qui fait couler la pluie, ou à cette route de montagne qui serpente jusqu'au sommet. Tous ces exemples sont des pentes. Savoir comment calculer une pente est donc une compétence beaucoup plus pratique qu'on ne le pense.
Pourquoi ce calcul est-il si important?
Bien maîtriser ce calcul ouvre la porte à plein d'applications concrètes, loin des examens. Dans la vraie vie, une pente bien calculée est une question de sécurité et d'efficacité.
- Construction: Pour un toit, la bonne pente assure que l'eau s'évacue correctement, ce qui évite les infiltrations et les dommages à la structure.
- Aménagement paysager: Elle est essentielle pour créer des allées accessibles et des terrasses qui tiennent bien sur un terrain en relief.
- Sécurité routière: La conception des routes repose entièrement sur le calcul des pentes pour que les véhicules puissent monter et descendre sans danger.
Par exemple, en Californie, la gestion des routes en montagne est un enjeu majeur. Une pente de 10 % signifie qu'on s'élève de 10 mètres pour chaque 100 mètres parcourus horizontalement. Près de 35 % des routes rurales dans ces régions ont des pentes de plus de 8 %, ce qui exige des normes de construction extrêmement strictes pour la sécurité de tous. Pour en savoir plus sur ces applications, il est toujours intéressant de consulter des informations détaillées sur la topographie.
L'idée à retenir : La pente, c’est le lien entre le déplacement vertical (la hauteur qu’on gagne ou perd) et le déplacement horizontal (la distance qu’on parcourt au sol).
En saisissant ce principe tout simple, un problème de maths se transforme en un outil puissant pour observer et même modeler le monde qui nous entoure.
Comment calculer la pente? La formule expliquée
Pour vraiment comprendre comment calculer une pente, il faut d'abord apprivoiser la fameuse formule. Oubliez le jargon mathématique compliqué qui peut faire peur. La formule est en fait assez simple : m = (y2 – y1) / (x2 – x1).
Ici, « m » est le symbole qu'on utilise pour la pente. Les paires (x1, y1) et (x2, y2) ne sont rien de plus que les coordonnées de deux points sur une ligne droite. C'est tout!
Visualiser la formule pour mieux comprendre
Pour que ce soit plus concret, décomposons la formule. La partie (y2 – y1) est ce qu'on appelle la « montée » (ou l'élévation verticale). On la note parfois Δy, qui veut dire « variation en y ». En gros, elle mesure de combien on monte ou on descend quand on passe d'un point à l'autre.
L'autre partie, (x2 – x1), c'est la « course » (la distance horizontale). On la note Δx. Elle mesure la distance qu'on parcourt à plat entre ces deux mêmes points.
La pente, c'est donc simplement le rapport entre la montée (le déplacement vertical) et la course (le déplacement horizontal). C’est une façon de mesurer l'inclinaison d'une droite.
Ce petit schéma aide vraiment à voir comment tout ça fonctionne dans un plan cartésien.
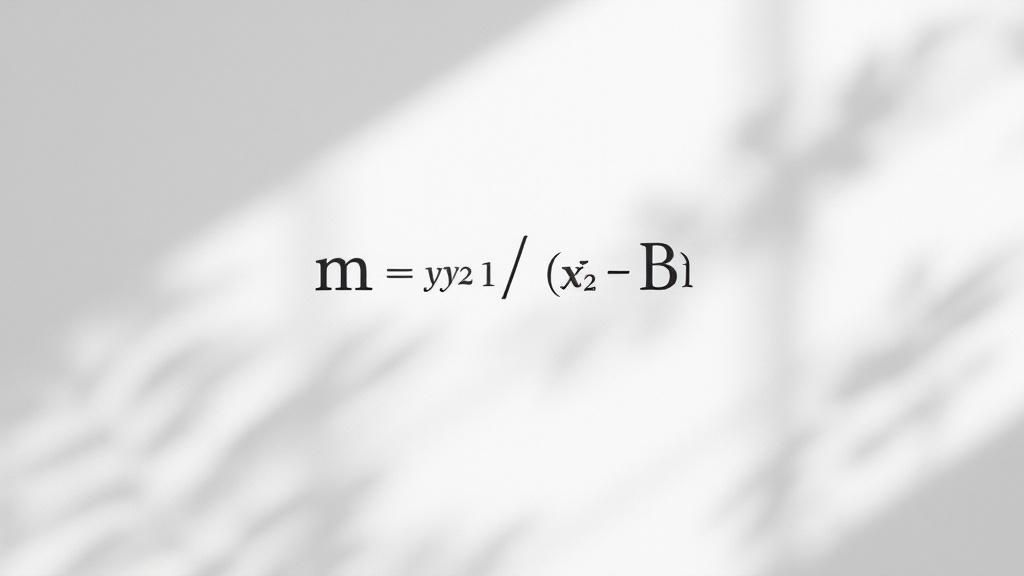
On voit bien que pour chaque déplacement horizontal (Δx), il y a un déplacement vertical (Δy) qui correspond. C'est ce duo qui définit l'inclinaison de la droite.
La formule en action : un exemple simple
Mettons la formule en pratique. Imaginez qu'on a deux points : le point 1 avec les coordonnées (2, 3) et le point 2 avec les coordonnées (6, 11).
- Calculons la montée (Δy) : On fait la différence des « y », soit 11 – 3 = 8.
- Calculons la course (Δx) : On fait la différence des « x », donc 6 – 2 = 4.
- Et enfin, la pente (m) : On divise la montée par la course, 8 / 4 = 2.
La pente est de 2. Ça veut dire que pour chaque pas qu'on fait vers la droite sur le graphique, on monte de deux pas.
Cette formule est un outil de base en mathématiques, mais si certains concepts vous semblent encore un peu flous, un coup de pouce personnalisé peut faire toute la différence. Le tutorat en maths est d'ailleurs une excellente façon de solidifier ces notions. Finalement, cette formule n'est qu'un moyen de mettre un chiffre sur une idée très visuelle.
Calculer une pente avec un exemple du monde réel
Rien de tel que de passer de la théorie aux exemples concrets pour vraiment assimiler une notion. Pour bien maîtriser comment calculer la pente, mettons la formule en pratique avec un scénario simple : déterminer l'inclinaison d'une rampe d'accès pour fauteuil roulant.
Disons que la base de la rampe (le Point A) se trouve aux coordonnées (2, 1) et que son sommet (le Point B) est situé à (8, 4). Dans cet exemple, chaque unité sur notre graphique représente un mètre.
Appliquer la formule étape par étape
La première chose à faire est de trouver ce qu'on appelle la « montée », c'est-à-dire la différence de hauteur sur l'axe vertical. On y arrive en soustrayant la coordonnée y du point de départ de celle du point d'arrivée.
- Calcul de la montée (Δy) : 4 – 1 = 3 mètres.
Ensuite, on fait exactement la même chose pour la « course », qui correspond à la distance horizontale. On soustrait la coordonnée x du premier point de celle du second.
- Calcul de la course (Δx) : 8 – 2 = 6 mètres.
Il ne reste plus qu'à diviser la montée par la course pour obtenir la pente. Le calcul est tout simple : 3 divisé par 6, ce qui nous donne 0,5. Ce chiffre représente le rapport d'inclinaison de notre rampe.
Le conseil du pro : L'ordre dans lequel vous choisissez vos points est crucial. Si vous aviez pris (8, 4) comme point 1 et (2, 1) comme point 2, votre calcul aurait été (-3) / (-6), ce qui donne aussi 0,5. L'important, c'est de garder le même ordre pour les coordonnées x et y. La constance est la clé!
L'infographie ci-dessous illustre parfaitement ce calcul. On y voit clairement comment les coordonnées des points A et B permettent de définir la montée et la course sur un plan quadrillé.
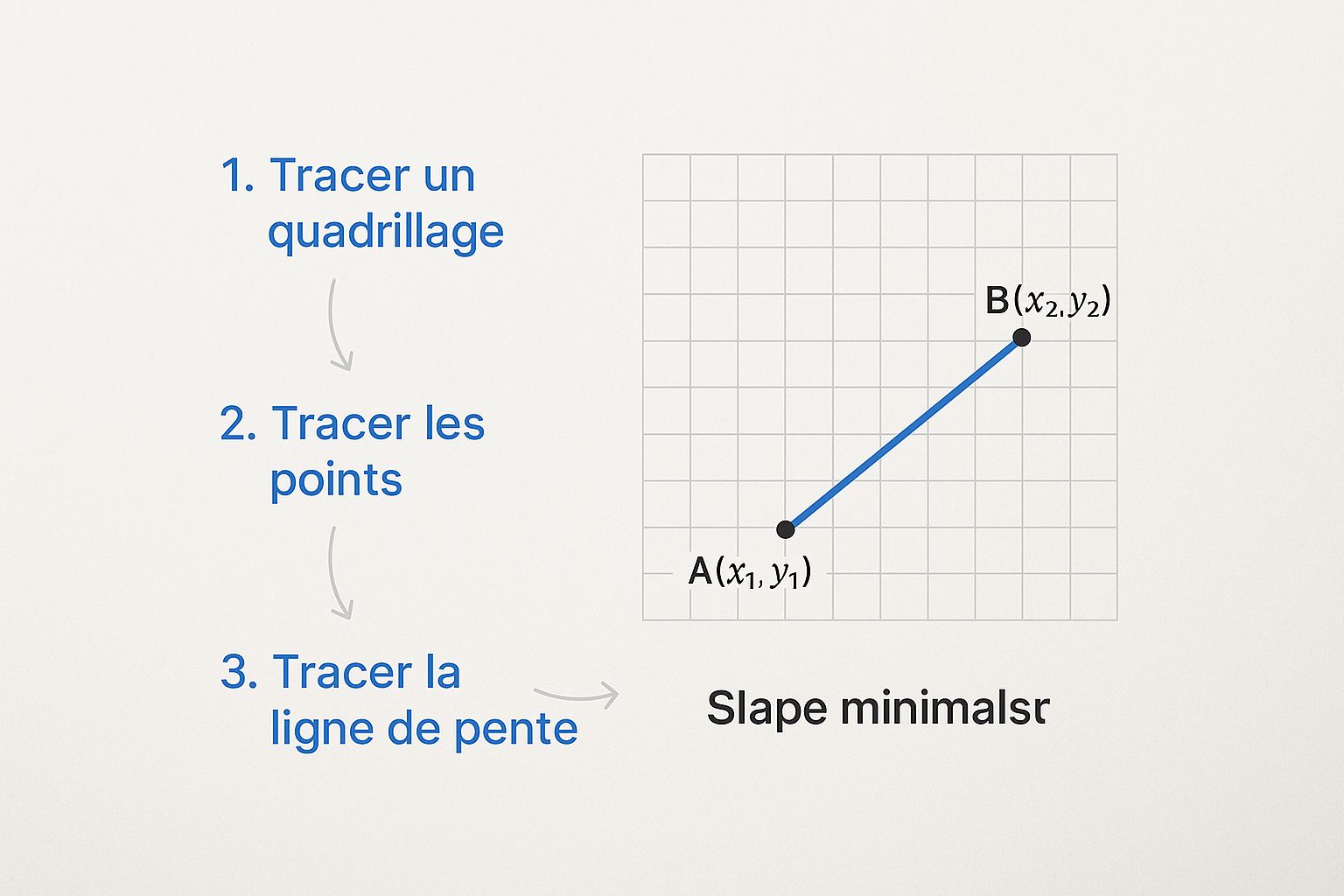
Ce genre de visuel aide à comprendre que la pente n'est finalement que le rapport entre le déplacement vertical et le déplacement horizontal d'un objet.
Transformer le résultat en pourcentage
Un rapport de 0,5, qu'est-ce que ça veut dire concrètement? Pour que ce chiffre soit plus parlant, on a l'habitude de le convertir en pourcentage. C'est facile, il suffit de le multiplier par 100. Dans notre cas : 0,5 x 100 = 50 %. Notre rampe a donc une pente de 50 %.
Cette application pratique du calcul de pente est utile dans une foule de domaines, bien au-delà des rampes d'accès. Par exemple, la pente des toits est un facteur déterminant pour l'efficacité des panneaux solaires. Une toiture avec une pente de 15 % à 30 % est souvent considérée comme idéale pour maximiser l'exposition au soleil. En fait, environ 60 % des installations solaires se font sur des toits avec une pente moyenne de 20 % pour trouver le meilleur équilibre.
Savoir appliquer cette formule à des situations réelles est une compétence tout aussi utile que de calculer le volume d’un cône facilement avec notre guide complet.
Donner un sens à vos résultats de calcul
Obtenir un chiffre après un calcul, c’est bien. Mais comprendre ce que ce résultat signifie vraiment, c'est là que les maths prennent tout leur sens. Une fois que vous maîtrisez comment calculer la pente, l'étape suivante, c'est de savoir l'interpréter correctement.
La valeur que vous obtenez vous raconte une histoire très visuelle sur la direction et l'inclinaison de votre ligne. C'est beaucoup plus simple qu'on ne le pense au premier abord.
Comprendre les différents types de pentes
Chaque résultat possible correspond à un scénario bien précis.
Une pente positive indique que la ligne monte en allant de la gauche vers la droite. Imaginez un sentier de randonnée qui grimpe une colline. Plus le chiffre est grand, plus la montée est raide!
Au contraire, une pente négative signifie que la ligne descend, un peu comme une piste de ski qui dévale la montagne. Un chiffre comme -2 indique une descente deux fois plus abrupte qu'une pente de -1.
Une pente nulle, donc égale à zéro, représente une surface parfaitement plate. Pensez à un plancher, une patinoire ou une route droite en Beauce. Il n'y a ni montée, ni descente.
Il existe aussi un cas particulier : la pente indéfinie. Ça arrive quand la ligne est complètement verticale, comme un mur. Le calcul demanderait de diviser par zéro, ce qui est impossible en mathématiques. C'est pour ça qu'on la qualifie d'« indéfinie ».
Interprétation des valeurs de pente
Pour vous aider à visualiser rapidement, voici un petit tableau qui résume tout. C'est un excellent aide-mémoire pour comprendre en un clin d'œil ce que votre résultat veut dire.
| Valeur de la pente | Signification | Direction de la ligne | Exemple visuel |
|---|---|---|---|
| Positive (ex: 2) | La ligne monte | Croissante (vers le haut) | Une côte à vélo |
| Négative (ex: -0.5) | La ligne descend | Décroissante (vers le bas) | Une rampe de garage |
| Nulle (0) | La ligne est plate | Horizontale | Un terrain de soccer |
| Indéfinie | La ligne est verticale | Verticale | Un mur d'escalade |
Ces concepts sont la base de plusieurs chapitres en mathématiques, mais leur utilité va bien au-delà de la salle de classe.
Ces notions sont fondamentales en mathématiques, mais savoir les appliquer concrètement est encore plus important. Si vous cherchez d'autres astuces pour transformer la théorie en pratique, notre article sur comment aider son enfant à réussir ses devoirs de mathématiques pourrait vous donner d'excellentes pistes.
À quoi sert le calcul de la pente dans la vraie vie?
On pourrait croire que de savoir comment calculer la pente est une notion purement scolaire, mais détrompez-vous! C'est une compétence qui a une valeur bien réelle et qui influence directement notre quotidien. Loin d’être un simple concept mathématique, ce calcul est au cœur de nombreux métiers et décisions qui garantissent notre sécurité et notre confort.
Pensez à la construction d'une maison. Une pente bien calculée est essentielle pour s'assurer que l'eau de pluie s'écoule loin des fondations. C'est ce qui prévient les infiltrations d'eau et les dommages coûteux à la structure du bâtiment.
Un outil crucial en urbanisme et en génie civil
En génie civil, l'importance du calcul de la pente est encore plus évidente. C'est grâce à lui qu'on conçoit des routes sécuritaires, avec des inclinaisons qui conviennent à tous les types de véhicules. Il est aussi fondamental pour la création de réseaux d’égouts qui fonctionnent sans problème.
L'aménagement paysager n'y échappe pas non plus. Le calcul de la pente permet de créer des jardins en terrasses qui sont stables, des allées agréables à emprunter, ou encore des systèmes de drainage efficaces pour protéger les terrains contre l'érosion.
Prenons l'exemple de Los Angeles. Les urbanistes s'appuient constamment sur ce calcul pour la conception des systèmes de drainage. Une pente trop faible (moins de 2 %) peut causer des inondations, alors qu'une inclinaison trop forte (plus de 10 %) augmente les risques d'érosion. Comme environ 40 % des terrains de la ville ont des pentes entre 5 % et 12 %, des solutions d'ingénierie précises, comme des murs de soutènement, sont souvent nécessaires.
Saviez-vous qu'en économie, la pente est aussi utilisée? Elle est fondamentale pour analyser les dynamiques du marché et les facteurs d'augmentation des prix, ce qui permet de visualiser clairement les tendances et leurs causes.
En voyant ces exemples concrets, on comprend vite que le calcul de la pente est bien plus qu'un exercice de maths. C’est une compétence pratique qui nous aide à construire un environnement plus sécuritaire, fonctionnel et durable pour tout le monde.
Cette compétence est d'ailleurs l'une des nombreuses notions où un petit coup de pouce peut faire toute la différence. Si vous souhaitez renforcer ces bases, découvrez les 5 bonnes raisons d'opter pour le tutorat dès le début de l'année scolaire.
Foire aux questions sur le calcul de la pente
Pour éclaircir les derniers points qui pourraient vous trotter dans la tête, voici les réponses aux questions les plus courantes sur le calcul de la pente. Chaque explication est simple, directe et vient compléter ce que nous avons déjà exploré ensemble.
Quelle est la différence entre la pente et l'angle d'inclinaison?
C'est facile de les mélanger, mais la pente et l'angle sont deux concepts bien distincts. La pente est un rapport, souvent exprimé en pourcentage (%), qui met en relation la montée (la hauteur verticale) et la course (la distance horizontale). C'est une mesure très concrète, idéale pour des applications pratiques comme la construction d'une route ou la planification d'un drainage.
L'angle, de son côté, se mesure en degrés (°). Il décrit la même inclinaison, mais d'une autre façon. Même s'il est possible de convertir l'un en l'autre grâce à la trigonométrie, la pente en pourcentage est souvent bien plus facile à visualiser dans la vie de tous les jours, que ce soit pour une rampe d'accès ou l'écoulement de l'eau.
Puis-je calculer la pente sans avoir de coordonnées exactes?
Absolument! La formule qui utilise les coordonnées (x, y) est un excellent outil, mais le principe derrière est encore plus simple. Si vous n'avez pas de coordonnées, vous pouvez toujours calculer la pente en mesurant directement deux choses :
- La hauteur verticale (ce qu'on appelle la « montée »).
- La distance horizontale (la « course »).
Prenons un exemple concret : une rampe s'élève de 1 mètre sur une distance horizontale totale de 10 mètres. Sa pente est simplement 1 divisé par 10, ce qui donne 0,1. On multiplie ce chiffre par 100 pour obtenir une pente de 10 %. C'est aussi simple que ça!
L'essentiel à retenir, c'est que la pente est toujours le rapport entre la variation verticale et la variation horizontale. Peu importe comment vous obtenez ces deux mesures, le principe de base ne change jamais.
Les maths peuvent parfois sembler un peu abstraites, mais elles décrivent des situations bien réelles. D'ailleurs, si vous voulez animer une discussion en classe ou avec des amis, lancer quelques questions brise-glace est une excellente façon de relier les concepts mathématiques au monde qui nous entoure.
Comment savoir si une pente respecte les normes d'accessibilité?
Voilà un point essentiel et non négociable. Les normes d'accessibilité, notamment pour les personnes à mobilité réduite, sont très précises. Une rampe d'accès dans un lieu public, par exemple, ne doit généralement pas avoir une pente supérieure à 5 %. Concrètement, cela veut dire une montée de 5 cm pour chaque mètre de distance horizontale.
Pour les rampes plus longues, la réglementation exige même des paliers de repos à intervalles réguliers. Avant de commencer le moindre projet, il est donc crucial de calculer votre pente et de la comparer aux normes locales. C'est une question de sécurité et de conformité légale.
Chez Centrétudes, nous sommes convaincus que la maîtrise des concepts mathématiques comme le calcul de la pente est fondamentale pour la réussite scolaire et bien plus encore. Nos tuteurs certifiés sont là pour transformer les défis en confiance. Découvrez notre approche personnalisée.


