Vous voulez savoir comment calculer un pourcentage d'augmentation? C'est plus simple qu'il n'y paraît. La formule clé à retenir est la suivante : [(Nouvelle valeur – Ancienne valeur) / Ancienne valeur] x 100.
Cette formule vous permet de mesurer précisément une évolution entre deux nombres. C'est un outil pratique pour tout, que ce soit pour suivre la hausse d'un prix, évaluer une progression dans vos notes ou analyser des données professionnelles.
La formule simple pour calculer une augmentation
Plongeons dans le vif du sujet. Loin d'être complexe, cette formule repose sur une logique assez intuitive. On calcule d'abord l'écart entre le point de départ et le point d'arrivée, puis on rapporte cet écart à la valeur initiale pour voir ce que ça représente en proportion.

Pour que ce soit plus parlant, prenons un cas que tout élève connaît : une note qui grimpe de 12/20 à 15/20. On sent bien qu'il y a une amélioration, mais de combien exactement, en pourcentage? C'est là que la formule entre en jeu.
Calculer un pourcentage d'augmentation en 3 étapes
Pour bien visualiser le processus, rien ne vaut un tableau qui décompose la formule en actions simples. Cette approche étape par étape vous aidera à appliquer le calcul sans vous tromper, peu importe les chiffres.
| Étape | Action à réaliser | Exemple (une note passe de 12 à 15) |
|---|---|---|
| 1. Calculer la différence | Soustraire l’ancienne valeur de la nouvelle valeur. | 15 – 12 = 3 |
| 2. Diviser par la valeur initiale | Diviser le résultat obtenu par la valeur de départ. | 3 / 12 = 0,25 |
| 3. Convertir en pourcentage | Multiplier le résultat final par 100. | 0,25 x 100 = 25 % |
Voilà, le résultat est clair et net : la note a connu une augmentation de 25 %. C'est aussi simple que ça!
Cette méthode en trois temps est universelle. Que vous analysiez la hausse du prix de votre café préféré ou l’amélioration de vos performances sportives, la logique reste la même. L'essentiel est de toujours diviser par la valeur initiale.
Savoir faire ce calcul est une compétence de base, utile bien au-delà des cours de maths. Si vous sentez que vous avez besoin de solidifier vos connaissances, un service de tutorat en mathématiques peut vous offrir un accompagnement personnalisé pour gagner en confiance.
En maîtrisant cette formule, vous vous dotez d'un outil puissant pour mieux comprendre et analyser le monde qui vous entoure.
Mettre la formule en pratique avec des exemples du quotidien
Les mathématiques prennent tout leur sens quand on les applique à la vraie vie. Le calcul de pourcentage n'y échappe pas. Mettre des chiffres sur les augmentations qu'on voit tous les jours, ça aide à vraiment saisir leur impact.

Prenons un exemple que plusieurs connaissent : le prix d’un jeu vidéo neuf qui grimpe de 50 $ à 60 $. On applique la formule. D'abord, on trouve la différence (60 $ – 50 $ = 10 $). Ensuite, on divise cette différence par le prix de départ (10 $ / 50 $ = 0,20). On multiplie par 100, et voilà : une augmentation de 20 %.
Cette logique s'applique partout, autant pour gérer son budget personnel que pour piloter une entreprise. Dans certains domaines, c'est même un outil de travail essentiel. En restauration, par exemple, les gestionnaires doivent savoir comment calculer le food cost pour s'assurer que leurs marges sont bonnes.
Analyser une hausse de forfait mobile
Imaginons que votre forfait de cellulaire mensuel passe de 35 $ à 42 $. De combien est l'augmentation, en pourcentage? On y va étape par étape :
- Calculer l'écart : 42 $ – 35 $ = 7 $
- Diviser par la valeur initiale : 7 $ / 35 $ = 0,20
- Convertir en pourcentage : 0,20 x 100 = 20 %
Votre forfait a donc augmenté de 20 %. Ce chiffre est bien plus parlant qu'une simple augmentation de 7 $ et vous aide à mieux évaluer l'impact sur vos finances.
Mesurer une progression personnelle
Ce calcul ne sert pas qu'à l'argent. C'est aussi un super outil pour mesurer ses propres progrès, que ce soit en lecture, au gym ou dans ses études. Si un élève voit sa note en maths passer de 60 % à 75 % après quelques semaines de soutien, on peut chiffrer cette belle amélioration.
(75 – 60) ÷ 60 x 100 = 25 %
On ne parle pas juste de 15 points de plus, mais bien d'une amélioration de 25 % de sa note. C'est une donnée concrète et vraiment motivante qui prouve que les efforts portent fruit. C'est d'ailleurs ce genre de progrès mesurable qui montre l'efficacité d'un accompagnement personnalisé comme le tutorat et l'aide aux devoirs en maths.
Au Québec, cette compétence nous aide même à décoder des enjeux de société. À Montréal, par exemple, le taux de diplomation au secondaire est passé de 72,3 % en 2009 à 83,9 % en 2022. C'est une progression énorme! Ces exemples montrent bien à quel point savoir comment calculer un pourcentage d'augmentation est une compétence utile dans toutes les sphères de notre vie.
Attention à l’erreur fréquente : pourcentage et points de pourcentage
C'est une confusion classique, mais elle peut complètement fausser vos conclusions. Pour bien interpréter les données, il est essentiel de comprendre la différence entre une augmentation en pourcentage (une mesure relative) et une augmentation en points de pourcentage (une mesure absolue).

Prenons un exemple concret pour bien saisir la nuance. Imaginez que le taux de réussite à un examen important passe de 80 % à 85 % d’une année à l’autre. Comment décrire cette progression?
La différence entre les deux calculs
Intuitivement, on serait tenté de dire qu'il y a eu une augmentation de 5 %. Ce n’est pas tout à fait faux, mais il faut être précis. Il s’agit en fait d’une hausse de 5 points de pourcentage. C'est une simple soustraction : 85 – 80 = 5. C’est la différence directe entre les deux pourcentages.
Maintenant, si on veut connaître le véritable pourcentage d'augmentation de la performance, on doit ressortir notre formule.
- Valeur initiale : 80
- Nouvelle valeur : 85
- Calcul : [(85 – 80) / 80] x 100 = (5 / 80) x 100 = 0,0625 x 100 = 6,25 %
Le taux de réussite a donc augmenté de 6,25 %, même si l'écart n'est que de 5 points de pourcentage. Le résultat n’est pas du tout le même!
La règle d’or à retenir
Les points de pourcentage mesurent la différence arithmétique entre deux pourcentages (une simple soustraction). Le pourcentage d’augmentation, lui, mesure l’évolution relative par rapport à la valeur de départ.
Cette distinction est cruciale pour analyser des statistiques, que ce soit dans les nouvelles ou pour évaluer des progrès scolaires. Ne pas les mélanger permet d'éviter des interprétations erronées et de mieux comprendre la portée réelle d'une évolution. Cette compétence mathématique, applicable dans de nombreux contextes, est un atout précieux, et un tutorat pour toutes les matières peut aider à renforcer ces notions fondamentales.
Appliquer le calcul à des données réelles du Québec
Une formule mathématique, ça prend vraiment vie quand on l'applique à des situations concrètes. Pour bien saisir comment calculer un pourcentage d'augmentation, rien de tel que de se plonger dans des statistiques bien de chez nous. C'est en manipulant des chiffres qui nous parlent que le concept devient limpide.
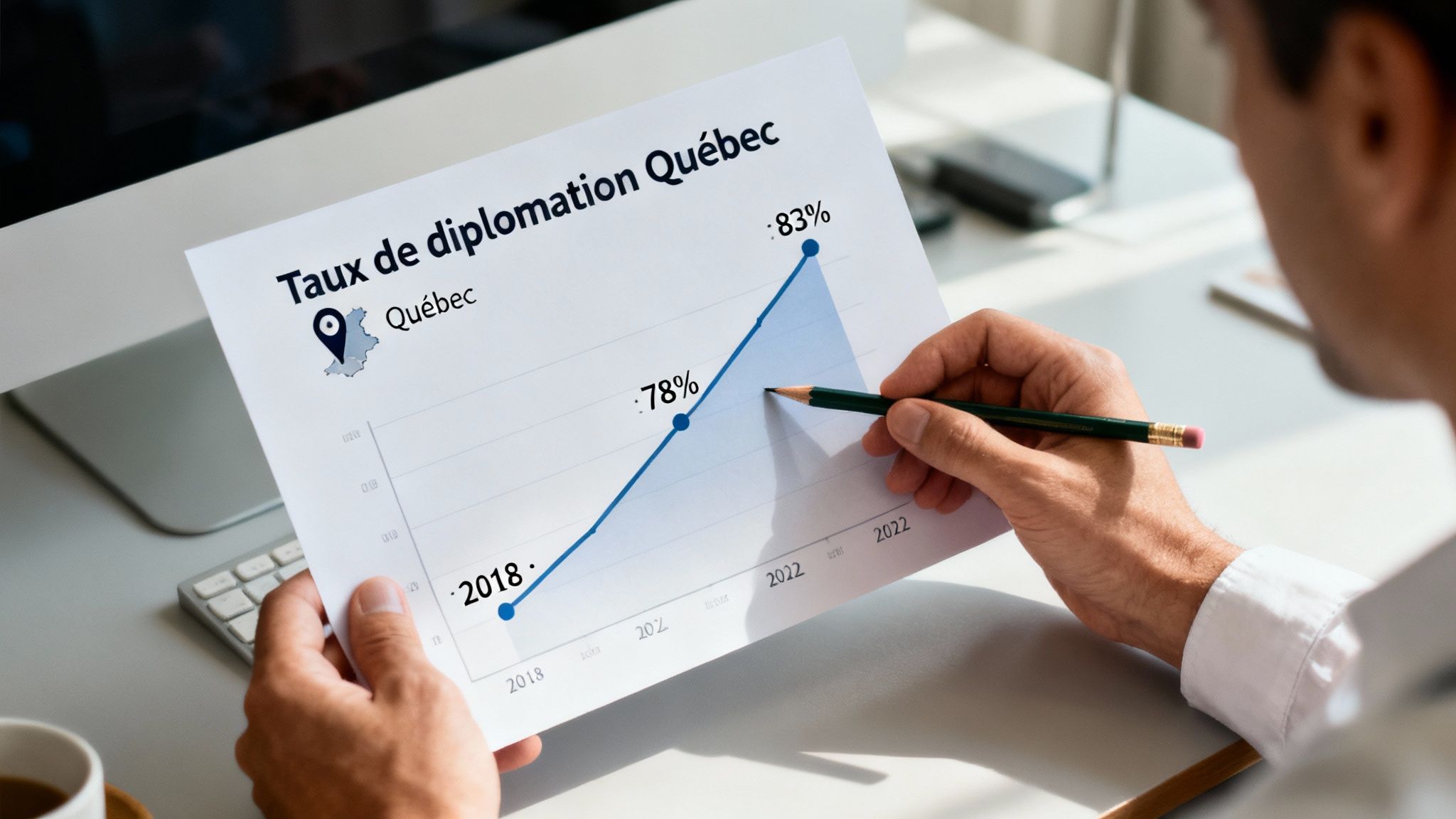
Imaginez devoir suivre l'évolution du taux de réussite scolaire dans votre région. Ces chiffres ne sont pas juste des données abstraites; ils racontent une histoire, celle des tendances en éducation qui nous touchent directement.
Un cas pratique avec les données de Statistique Canada
Prenons un exemple parlant : le taux de diplomation au secondaire. Selon les données officielles, ce taux au Canada est passé de 88 % en 2015-2016 à 89 % l'année suivante. À première vue, on pourrait se dire qu'une hausse de 1 point de pourcentage, c'est peu.
Mais voyons ce que ça donne avec notre formule :
- On calcule la différence : 89 – 88 = 1
- On divise par la valeur de départ : 1 ÷ 88 ≈ 0,01136
- On convertit en pourcentage : 0,01136 x 100 ≈ 1,14 %
Le taux a donc réellement augmenté de 1,14 % en un an. Ce calcul nous donne une bien meilleure idée de la dynamique derrière les chiffres. Pour les curieux, toutes ces données éducatives détaillées sont sur le site de Statistique Canada.
Cet exercice nous montre bien qu'une petite variation en points peut cacher une évolution plus significative qu'il n'y paraît. D'ailleurs, entre 2013 et 2017, le Québec a connu l'une des plus fortes hausses au pays avec un gain de 4 points de pourcentage.
C'est un peu comme à l'école : gagner quelques points à un examen peut représenter une augmentation importante de la performance d'un élève. C'est une façon très concrète de mesurer le progrès et de valoriser les efforts.
Dans le monde des affaires, ce même type de calcul est utilisé constamment. Les entreprises qui analysent leurs données avec des systèmes CRM/ERP personnalisés suivent des logiques de croissance très similaires pour mesurer leur performance.
Savoir manier cette formule avec des chiffres réels, ce n'est pas juste utile en maths. Ça développe aussi notre esprit critique pour mieux comprendre l'information chiffrée qu'on nous présente tous les jours.
Quelques outils et astuces pour vérifier vos calculs rapidement
Connaître la formule, c'est bien. Être absolument certain de son résultat, c'est encore mieux! Heureusement, il existe quelques techniques toutes simples pour valider un calcul en un clin d'œil et repérer une erreur avant qu'elle ne devienne un problème. Ces astuces vous aideront à développer de bons réflexes en mathématiques.
La toute première étape, et peut-être la plus importante, c'est l'estimation mentale. Avant même de sortir votre calculatrice, prenez une seconde pour évaluer l'ordre de grandeur du résultat attendu. Par exemple, si un prix passe de 50 $ à 70 $, vous savez instinctivement que l'augmentation est de 20 $. Puisque 50 % de 50 $, c'est 25 $, votre réponse finale doit forcément être un peu inférieure à 50 %.
Cette petite anticipation agit comme un garde-fou. Si votre calcul final vous donne un résultat qui semble absurde, comme 80 % ou 2 %, vous saurez immédiatement qu'une erreur s'est glissée quelque part.
Utiliser la calculatrice efficacement
Votre téléphone ou votre calculatrice de bureau possède des fonctions bien pratiques pour vérifier un pourcentage d'augmentation. Plutôt que d'enchaîner les opérations une par une, pourquoi ne pas utiliser directement la touche pourcentage (%)?
Par exemple, pour vérifier une hausse de 25 % sur un montant de départ de 80 $ :
- Tapez simplement 80 + 25 %.
- La calculatrice affichera directement le résultat final, soit 100 $.
Non seulement c'est plus rapide, mais ça diminue aussi grandement le risque de faire une petite faute de frappe en recopiant les résultats intermédiaires.
Une autre technique très efficace est le calcul inversé. Imaginez que vous avez calculé qu'une valeur de 150 $ augmentée de 20 % donne 180 $. Pour vérifier, partez de la fin! Prenez votre résultat (180 $) et divisez-le par (1 + le pourcentage en décimal), donc par 1,20. Le calcul 180 / 1,20 devrait vous ramener à votre point de départ : 150 $. Si c'est le cas, bravo, votre calcul est juste!
Ces petits réflexes de vérification sont essentiels pour bâtir sa confiance en mathématiques. Si ces concepts vous semblent encore un peu flous, un service de tutorat et d'aide aux devoirs en ligne peut offrir des explications personnalisées pour vous aider à les maîtriser complètement.
Vos questions fréquentes sur le calcul de pourcentage
Même avec la formule bien en tête, certaines situations particulières peuvent prêter à confusion. C'est tout à fait normal. Démystifions ensemble quelques cas de figure pour que le calcul d'augmentation n'ait plus aucun secret pour vous.
Cette section est là pour éclaircir les derniers points d'ombre et aborder les questions qui reviennent le plus souvent.
Peut-on calculer une augmentation avec une valeur de départ négative?
Techniquement, oui. La formule mathématique s'applique. Si la température passe de -10 °C à -5 °C, le calcul serait : [(-5 - (-10)) / -10] x 100, ce qui donne un résultat de -50 %.
Le problème? C'est totalement contre-intuitif. On parle bien d'un réchauffement, donc d'une amélioration, mais le résultat est négatif. Pour éviter ce genre de casse-tête, rassurez-vous : dans un contexte scolaire ou pratique, vous travaillerez presque toujours avec des valeurs positives, où le résultat a un sens logique et direct.
Comment gérer des augmentations successives?
Attention, c'est un piège classique! L'erreur la plus commune est d'additionner les pourcentages. Or, chaque nouvelle augmentation s'applique sur la nouvelle valeur, pas sur celle d'origine.
Imaginez un produit qui coûte 100 $. Il augmente de 10 %, son prix grimpe donc à 110 $. Si, plus tard, il subit une deuxième hausse de 20 %, ce nouveau pourcentage se calcule sur les 110 $. L'augmentation est donc de 22 $ (20 % de 110 $). Au total, le prix a augmenté de 10 $ + 22 $ = 32 $. L'augmentation totale est donc de 32 %, et non de 30 % (10 % + 20 %).
Quelle est la différence avec le calcul d'une réduction?
La logique de base est identique : on compare toujours la différence à la valeur de départ. La formule est juste un peu ajustée pour obtenir un résultat positif : [(Valeur initiale - Valeur finale) / Valeur initiale] x 100.
Le point crucial à retenir, que ce soit pour une hausse ou une baisse, c'est qu'on divise toujours par la valeur initiale. C'est elle qui sert de point de référence pour mesurer l'évolution.
Que faire si je n'ai que la valeur finale et le pourcentage d'augmentation?
Excellent exercice! Il s'agit simplement d'un calcul inversé. Pour retrouver la valeur d'origine, il suffit de diviser la valeur finale par (1 + le pourcentage d'augmentation exprimé en décimal).
Par exemple, un article coûte 120 $ après une augmentation de 20 % (soit 0,20). Pour trouver le prix initial, le calcul est : 120 / (1 + 0,20) = 120 / 1,20 = 100 $. Et voilà, vous avez retrouvé la valeur de départ!
Si d'autres questions vous viennent à l'esprit ou si certains concepts restent flous, n'hésitez jamais à demander de l'aide. Pour toute demande d'informations sur nos services, vous pouvez nous contacter directement.
Chez Centrétudes, nous transformons les doutes en confiance. Si les pourcentages ou d'autres notions mathématiques représentent un défi, nos tuteurs certifiés offrent un accompagnement personnalisé pour aider chaque élève à réussir.


