En géométrie, le diamètre d'un cercle est une notion de base, mais absolument essentielle. Pour faire simple, c'est la plus grande distance en ligne droite qu'on peut mesurer d'un bord à l'autre d'un cercle, à condition de passer pile par le centre. C'est ce qui définit sa largeur maximale.
Qu'est-ce que le diamètre d'un cercle?
Imaginez que vous coupez une pizza en deux parts parfaitement égales. La ligne de coupe que vous venez de faire, c'est exactement ça, le diamètre. C'est un segment de droite qui joint deux points opposés sur le bord du cercle en traversant son cœur. Cette mesure est cruciale, car elle nous dit tout sur la taille du cercle.
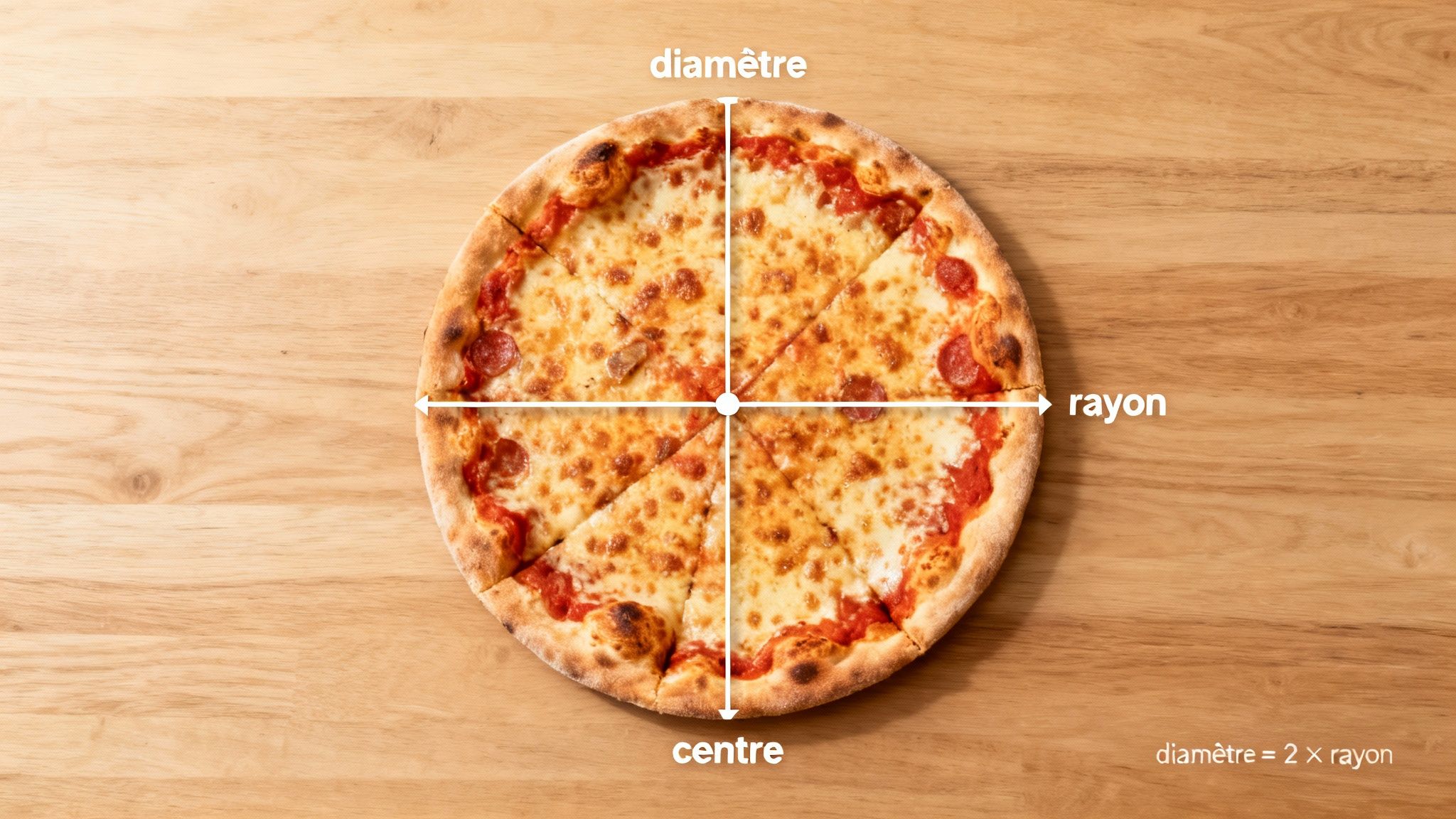
Pour bien saisir le concept de diamètre, il faut aussi connaître son acolyte indispensable : le rayon. Le rayon, c'est la distance entre le centre du cercle et n'importe quel point sur sa circonférence. La relation entre les deux est d'une simplicité désarmante :
Le diamètre est toujours et exactement le double du rayon. Si vous connaissez l'un, vous pouvez trouver l'autre en une fraction de seconde. La formule est toute simple : d = 2r.
Cette connexion est la première étape pour maîtriser la géométrie du cercle. Elle permet non seulement de comprendre les proportions de la figure, mais elle ouvre aussi la porte à des calculs plus complexes comme la circonférence et l'aire.
Les éléments clés du cercle
Pour visualiser encore mieux ces concepts, il est utile de les mettre côte à côte.
Les éléments clés du cercle en un coup d'œil
Ce petit tableau résume les composants fondamentaux du cercle et la façon dont ils interagissent. C'est une excellente base pour s'y retrouver.
| Concept | Description simple | Relation |
|---|---|---|
| Le Centre | Le point fixe au milieu du cercle. | Tous les points du cercle sont à égale distance du centre. |
| Le Rayon (r) | La distance du centre à n'importe quel point sur le bord. | C'est la moitié du diamètre (r = d/2). |
| Le Diamètre (d) | Le segment qui traverse le centre et relie deux points opposés. | C'est le double du rayon (d = 2r). |
La maîtrise de ces notions de base est la clé pour avancer sans difficulté. Si votre enfant bloque sur ces concepts, un accompagnement personnalisé en tutorat en mathématiques peut l'aider à bâtir une confiance solide et à surmonter les obstacles.
Le lien essentiel entre le diamètre, le rayon et la circonférence
Quand on parle de la largeur d'un cercle, comment cette mesure se compare-t-elle à la longueur totale de son contour? C'est là que trois concepts indissociables en géométrie entrent en scène : le diamètre, le rayon et la circonférence. Bien comprendre leur relation est la clé pour résoudre une foule de problèmes mathématiques.

La toute première relation, la plus directe, est celle qui unit le diamètre et le rayon. Comme on l'a vu, le diamètre traverse le cercle de part en part en passant par le centre. Le rayon, lui, ne fait que la moitié du chemin : du centre jusqu'au bord. La logique est donc assez simple :
Le diamètre (d) est toujours exactement le double du rayon (r).
La formule est donc : d = 2r
Cette petite formule est la base de nombreux calculs et un excellent point de départ pour quiconque s'aventure dans la géométrie du cercle.
De la largeur au contour
Maintenant, faisons entrer la circonférence (C) dans l'équation. C'est tout simplement le périmètre du cercle, autrement dit la distance totale si on en faisait le tour complet. Pensez à une roue de vélo : son diamètre est le rayon métallique qui traverse le moyeu, tandis que sa circonférence est la distance que la roue parcourt sur le sol en un seul tour.
C'est ici qu'un nombre célèbre entre en jeu : Pi (π). Depuis l'Antiquité, les mathématiciens ont fait une découverte fascinante : peu importe la taille du cercle, si on divise sa circonférence par son diamètre, on obtient toujours le même chiffre. Ce rapport constant, c'est Pi, dont la valeur est d'environ 3,14159.
Le lien magique est donc établi :
- La circonférence est toujours un peu plus de trois fois plus grande que le diamètre.
- Cette relation est fondamentale pour passer d'une mesure à l'autre sans effort.
Ces notions sont au cœur des programmes scolaires et leur maîtrise est cruciale, surtout pour les élèves qui préparent leurs évaluations. D'ailleurs, des ressources existent pour une préparation aux examens ministériels de 6e année en mathématiques qui permettent de renforcer ces compétences. En maîtrisant le lien entre diamètre, rayon et circonférence, les élèves s'assurent d'avoir un outil puissant pour la suite de leur parcours.
Les formules pour calculer le diamètre facilement
Aborder le calcul du diamètre d'un cercle est bien plus simple qu’on ne le pense. En réalité, deux formules principales permettent de trouver cette mesure clé, tout dépend de l’information que vous avez au départ. Aider votre enfant à maîtriser ces deux méthodes, c'est lui donner les outils pour résoudre la grande majorité des problèmes de géométrie liés au cercle.

La méthode la plus directe : à partir du rayon
Si vous connaissez déjà le rayon (r) d'un cercle, calculer le diamètre (d) devient un véritable jeu d'enfant. C'est la relation la plus fondamentale et, honnêtement, la plus facile à retenir.
La formule est tout simplement : d = 2 × r
Autrement dit, le diamètre, c'est ni plus ni moins que le double du rayon.
Par exemple, si le rayon d'une roue de vélo est de 30 cm, son diamètre sera de 2 × 30 cm = 60 cm. C’est une opération simple et directe qui ne demande aucune autre information.
L'astuce quand on connaît la circonférence
Parfois, la seule mesure que l'on a, c'est la longueur totale du contour du cercle, ce qu'on appelle sa circonférence (C). Dans ce cas-là, on fait appel à notre fameux ami, le nombre Pi (π ≈ 3,14).
La formule pour trouver le diamètre est alors : d = C / π
Imaginez que vous mesurez le contour d'une assiette et que vous obtenez 94,2 cm. Pour trouver son diamètre, il suffit de diviser cette valeur par Pi : 94,2 cm / 3,14 ≈ 30 cm. Le diamètre de votre assiette est donc d'environ 30 cm.
Cette compétence est un véritable pilier des mathématiques enseignées au Québec. Comprendre cette relation entre le diamètre et la circonférence est un tremplin vers plus d'autonomie dans la résolution de problèmes. Ces formules sont une excellente base pour aider lors des devoirs. Si jamais votre enfant a besoin d'un coup de pouce plus structuré, nos services de tutorat et aide aux devoirs en mathématiques peuvent offrir un accompagnement vraiment personnalisé.
Mettre les formules en pratique avec des exercices corrigés
Rien ne vaut la pratique pour vraiment maîtriser une notion de mathématiques. C'est le moment où la théorie du diamètre du cercle prend tout son sens. En se lançant dans des exercices progressifs, on transforme tranquillement les formules en outils concrets pour résoudre de vrais problèmes.

On va commencer tout doucement, avec des cas simples pour bâtir une confiance solide. Ensuite, on augmentera un peu la difficulté avec des scénarios plus engageants. Chaque problème est suivi d'une correction bien détaillée pour éclaircir non seulement la réponse, mais surtout le raisonnement derrière.
Exercice 1 : niveau primaire
Un élève du primaire adore son cerceau (hula hoop) dont le rayon mesure 40 centimètres. Il veut connaître sa largeur totale pour être certain d'avoir assez d'espace pour jouer sans tout accrocher. Quel est le diamètre de son cerceau?
- La bonne formule à utiliser : La plus simple et directe est celle qui relie le diamètre au rayon, c'est-à-dire d = 2 × r.
- Le calcul : Il suffit de multiplier le rayon par deux. On fait donc d = 2 × 40 cm.
- La réponse : Le diamètre du cerceau est de 80 centimètres.
Ce type d'exercice de base aide à ancrer l'idée que le diamètre, c'est tout simplement le double du rayon. C'est un réflexe essentiel à développer.
Exercice 2 : niveau secondaire
Pour un projet de jardinage, un adolescent doit installer une petite clôture autour d'un parterre de fleurs circulaire. Il mesure le tour complet et obtient une longueur de 18,84 mètres. Quel est le diamètre de ce parterre? (On va utiliser π ≈ 3,14 pour simplifier)
C'est un problème assez classique où la seule information qu'on a, c'est la circonférence. La clé, c'est de penser à l'envers et d'utiliser la relation entre le contour et la largeur du cercle.
Voici comment s'y prendre, étape par étape :
- Identifier la bonne formule : Comme on connaît la circonférence (C), on utilise la formule d = C / π.
- Appliquer les chiffres : On remplace C par 18,84 m et π par 3,14. Le calcul devient donc d = 18,84 / 3,14.
- Trouver la solution : Le diamètre du parterre de fleurs est de 6 mètres.
La maîtrise de ces calculs est vraiment importante, particulièrement pour les élèves au Québec. Bien comprendre le diamètre d'un cercle, ça développe une logique mathématique qui sera utile plus tard, que ce soit pour se préparer aux examens d'admission au secondaire ou même pour des épreuves au collégial. Par exemple, un élève qui doit calculer le tour d'un cercle de 20 cm de diamètre pour un projet de science est en train de renforcer des compétences en géométrie qui lui serviront tout au long de son parcours.
Si votre enfant trouve ces exercices un peu corsés, ne vous inquiétez pas, il existe des ressources pour l'aider. Vous pouvez par exemple jeter un œil à notre guide de préparation aux examens d'admission au secondaire pour trouver d'autres exercices et conseils pratiques.
Les erreurs fréquentes et nos conseils de tuteur
Même les notions les plus simples peuvent parfois donner du fil à retordre. En ce qui concerne le diamètre du cercle, certaines erreurs reviennent constamment chez les élèves. En tant que parent, savoir les repérer est le premier pas pour transformer un petit blocage en un déclic qui restera.
L’erreur la plus classique? Sans aucun doute la confusion entre le rayon et le diamètre. Un élève lit le mot « rayon » dans un problème, mais utilise la mesure comme si c'était le diamètre, ou l'inverse. Ça fausse évidemment tous les calculs qui suivent, que ce soit pour trouver la circonférence ou l'aire.
Une autre difficulté apparaît au moment d'appliquer les formules. Par exemple, un élève pourrait multiplier la circonférence par Pi au lieu de la diviser pour trouver le diamètre. Cette inversion des opérations montre souvent que la logique derrière la formule n'est pas encore bien installée.
Astuces de tuteur pour ne plus se tromper
Pour aider votre enfant à solidifier ses connaissances, voici quelques conseils pratiques, tout droit sortis de l'expérience de nos tuteurs.
- L’astuce des mots : Pour ne plus jamais mélanger rayon et diamètre, un petit truc tout simple : le mot « rayon » est plus court que « diamètre ». Ça tombe bien, car le segment du rayon est aussi plus court que celui du diamètre! C'est un moyen mnémotechnique facile à retenir.
- La manipulation avant tout : Prenez une assiette et un bout de ficelle. Mesurez concrètement le diamètre avec une règle, puis le contour (la circonférence) avec la ficelle. Montrez-lui de façon très visuelle que la ficelle est toujours environ trois fois plus longue que la règle. Cela ancre la formule
d = C / πdans le concret.
Un bon soutien, ce n'est pas donner la réponse, mais plutôt guider le raisonnement. Posez des questions comme : « Le diamètre, est-ce la plus grande ou la plus petite ligne droite dans le cercle ? » ou « Si le rayon, c'est la moitié, comment on ferait pour trouver le tout ? »
Ces petites stratégies rendent l'apprentissage plus interactif et beaucoup moins intimidant. Si les blocages persistent, l'accompagnement personnalisé offert par des tuteurs expérimentés peut fournir les outils nécessaires pour redonner confiance et assurer une compréhension profonde du diamètre du cercle.
Questions fréquentes sur le diamètre du cercle
Même après avoir exploré les formules et les exercices, il arrive souvent que quelques questions persistent. C’est tout à fait normal! Cette section a pour but de répondre aux interrogations les plus courantes pour dissiper les derniers doutes sur le diamètre du cercle.
Quelle est la différence entre un diamètre et une corde?
C'est une excellente question, car la distinction est importante. Imaginez un cercle. Une corde, c'est tout simplement un trait qui relie deux points sur le contour du cercle. Vous pourriez en tracer une infinité, de toutes les longueurs.
Le diamètre, lui, est une corde un peu spéciale. C'est la plus grande de toutes les cordes que l'on peut tracer dans un cercle. Sa particularité? Elle doit obligatoirement passer par le centre. En résumé : tous les diamètres sont des cordes, mais l'inverse n'est pas vrai.
Pourquoi Pi est-il si important pour le diamètre?
Le nombre Pi (π) est la clé magique qui relie la circonférence d'un cercle à son diamètre. C'est une constante universelle. Peu importe la taille du cercle – que ce soit un bouchon de bouteille ou la grande roue d'un parc d'attractions –, si vous divisez la longueur de son contour par sa largeur, vous tomberez toujours sur Pi (environ 3,14).
C’est cette relation immuable qui rend Pi indispensable en géométrie. Il nous permet de calculer la circonférence si on connaît le diamètre (C = π × d), et vice-versa. C'est un véritable pont entre ces deux mesures.
Comment puis-je aider mon enfant à mieux visualiser ce concept?
La meilleure façon d'apprendre la géométrie, c'est de la toucher! Laissez les manuels de côté un instant et partez à la chasse aux objets ronds dans la maison : une assiette, un couvercle de pot, une roue de petite voiture, un cerceau…
- Mesurez ensemble : Prenez une règle et trouvez le point le plus large de chaque objet pour mesurer le diamètre.
- Comparez concrètement : Ensuite, utilisez un ruban à mesurer souple pour faire le tour complet de l'objet (la circonférence).
- Faites le lien : Montrez à votre enfant que la longueur du ruban est toujours un peu plus de trois fois plus grande que la mesure de la règle. C'est ça, Pi!
Cette manipulation simple et concrète ancre la compréhension bien plus solidement qu'une formule abstraite apprise par cœur.
Chez Centrétudes, nous savons qu'un accompagnement personnalisé peut transformer un défi mathématique en une belle réussite. Découvrez comment nos tuteurs peuvent aider votre enfant à bâtir sa confiance sur https://centretudes.ca.


