La formule pour calculer l'aire d'un cylindre peut sembler intimidante au premier abord, mais elle est en réalité assez simple : A = 2πr(r + h). Essentiellement, cette équation additionne l'aire des deux bases circulaires avec celle de la surface latérale (le "corps" du cylindre).
Comprendre la logique derrière la formule
Pour bien saisir le concept, imaginez que vous déroulez l'étiquette d'une conserve. Vous vous retrouvez avec deux couvercles parfaitement ronds et une étiquette qui, une fois aplatie, forme un rectangle. La formule fait exactement ça : elle calcule la surface de chaque morceau, puis les additionne pour obtenir l'aire totale.

Cette visualisation est une base essentielle enseignée au Québec, car elle trouve des applications très concrètes dans les industries locales. Dans le secteur agroalimentaire, par exemple, optimiser la surface des contenants cylindriques peut réduire les coûts de matériaux de 12 % en moyenne.
Le tableau suivant décompose la formule de l'aire totale en ses deux parties principales pour une compréhension encore plus intuitive.
| Les composantes de la formule de l'aire du cylindre | ||
|---|---|---|
| Partie du cylindre | Formule | Rôle dans le calcul |
| Aire des deux bases circulaires | 2πr² | Calcule la surface combinée du "dessus" et du "dessous" du cylindre. |
| Aire de la surface latérale | 2πrh | Calcule la surface de la partie rectangulaire que l'on obtiendrait en "déroulant" le corps du cylindre. |
En combinant ces deux éléments (2πr² + 2πrh), et en simplifiant, on arrive à la fameuse formule A = 2πr(r + h).
Ce calcul est donc bien plus qu'une simple abstraction mathématique; c'est un outil pratique avec des répercussions réelles. Pour une explication plus approfondie, n'hésitez pas à consulter notre guide complet sur l'aire d'un cylindre. Vous pouvez aussi explorer d'autres applications et vous exercer avec des calculateurs en ligne comme celui de Omni Calculator.
Visualiser les éléments clés de la formule
Pour vraiment s'approprier la formule de l'aire d'un cylindre, il faut aller au-delà des lettres et des chiffres. La clé, c'est de visualiser ce que chaque partie représente concrètement.
Imaginez que vous prenez une canne de conserve et que vous en décollez l'étiquette. Qu'obtenez-vous? Un simple rectangle. C'est l'astuce pour que tout devienne clair. La longueur de ce rectangle correspond exactement à la circonférence du cercle de la base (2πr), et sa largeur n'est autre que la hauteur du cylindre (h). Ajoutez à cela les deux couvercles (les bases), qui sont tout simplement des cercles, et vous avez toutes les pièces du casse-tête.
Cette carte conceptuelle illustre bien comment le rayon et la hauteur sont les deux piliers de tout le calcul.
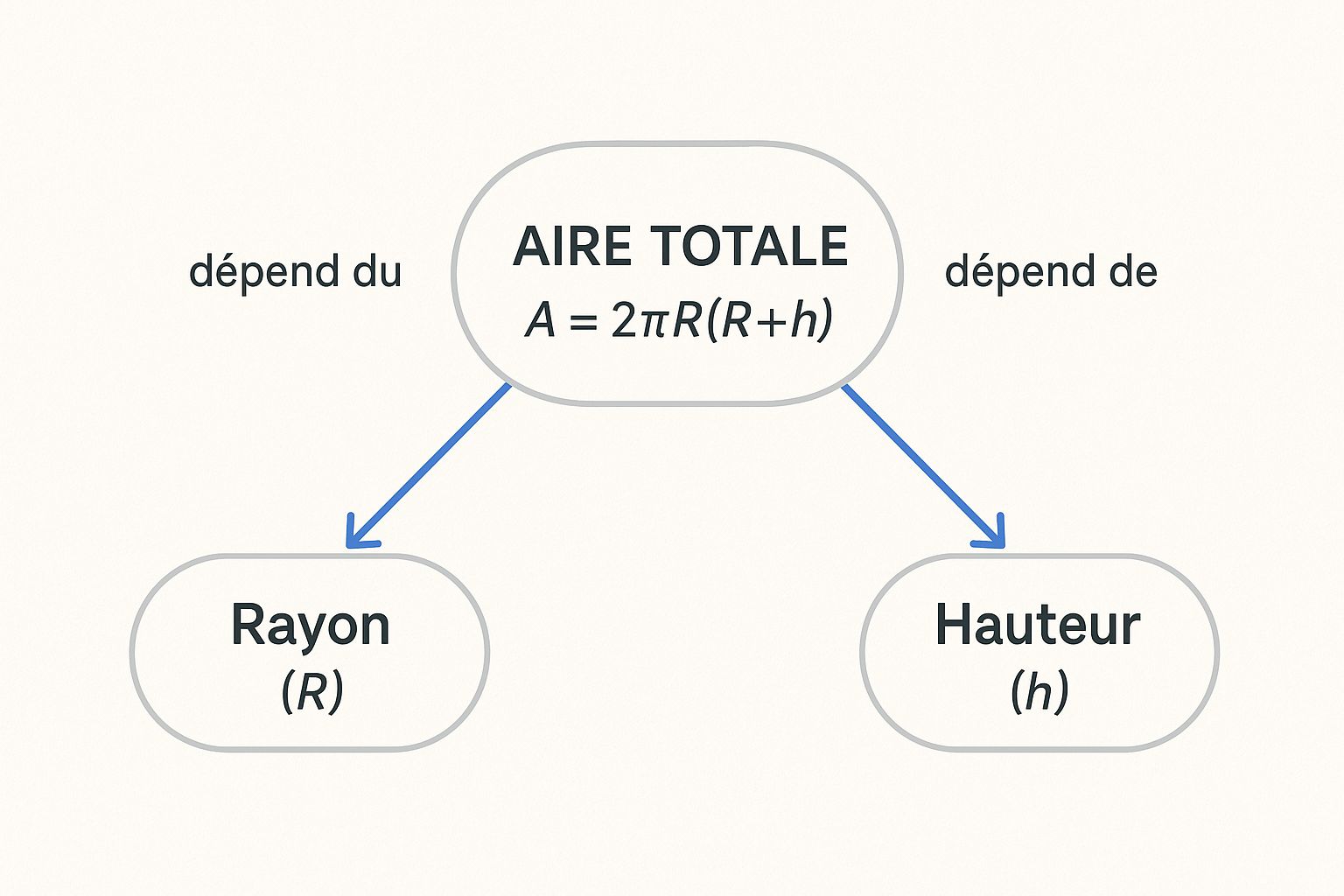
On y voit clairement que si l'on modifie l'une ou l'autre de ces mesures, c'est toute l'aire totale qui est directement affectée.
Le fait de transformer un objet 3D en une forme 2D à plat (ce qu'on appelle son "patron") rend un calcul qui semble abstrait beaucoup plus concret. C'est une technique toute simple, mais incroyablement efficace pour bien comprendre.
Si la visualisation des formes géométriques est un défi pour vous ou votre enfant, un service de tutorat en mathématiques peut vous donner des stratégies sur mesure pour solidifier votre compréhension et bâtir votre confiance.
Comment calculer l’aire latérale d’un cylindre
Concentrons-nous maintenant sur une seule partie du casse-tête : l’aire latérale. Imaginez simplement l'étiquette qui entoure une conserve. C'est ça, l'aire latérale! On la calcule avec la formule A_latérale = 2πrh.
Pour que ce soit plus concret, prenons l'exemple d'une étiquette de bouteille. Le processus se décompose en quelques étapes simples :
- On commence par mesurer le rayon (r) et la hauteur (h) de la bouteille.
- Ensuite, on insère ces deux valeurs directement dans la formule.
- On effectue le calcul pour trouver la surface exacte de l'étiquette. C'est tout!

Un détail crucial à ne jamais oublier est la cohérence des unités. Si vous mesurez le rayon en centimètres, assurez-vous que la hauteur l'est aussi. Cette petite vérification vous évitera bien des erreurs de calcul.
En vous exerçant sur cette partie spécifique, vous gagnerez en confiance pour aborder n'importe quel problème de cylindre. Si ces calculs vous semblent encore difficiles, nos services de tutorat et d'aide aux devoirs en maths peuvent offrir un soutien personnalisé pour vous aider à tout maîtriser.
Mettre la formule en pratique avec un exemple concret
Maintenant que nous avons toutes les pièces du puzzle, il est temps de les assembler. Appliquons la formule complète de l'aire du cylindre, soit A = 2πr² + 2πrh, à une situation bien réelle : estimer la quantité de tôle nécessaire pour construire un silo de stockage.
Imaginons un silo avec un rayon (r) de 5 mètres et une hauteur (h) de 15 mètres.
Pour ne pas s'emmêler dans les chiffres, le calcul se déroule en trois étapes simples et logiques.
- On calcule d'abord l'aire des deux bases (le sol et le toit du silo). Pour ça, on utilise la formule 2πr².
- Ensuite, on calcule l'aire latérale (la grande paroi courbée). Ici, on emploie la formule 2πrh.
- Finalement, on additionne les deux résultats. En combinant l'aire des bases et l'aire latérale, on obtient la surface totale de tôle dont on aura besoin.
Cette approche structurée permet de décomposer un problème qui semble complexe en une série de petits calculs faciles à gérer. C'est une compétence essentielle pour réussir n'importe quel test, y compris un examen d'admission au secondaire.
Voir la formule en action dans le monde réel
Cette formule mathématique peut sembler abstraite, mais elle est bien plus qu'un simple exercice scolaire. En réalité, ses applications pratiques façonnent notre quotidien. On la retrouve partout, que ce soit pour concevoir des réservoirs, optimiser des emballages ou même estimer les matériaux nécessaires pour des colonnes décoratives.

Dans chacun de ces cas, un calcul précis a un impact direct sur les coûts, l'efficacité et la durabilité d'un projet. C'est du concret!
Au Québec, cette compétence est d'ailleurs jugée essentielle, surtout pour les professions techniques qui sont en pleine croissance. Saviez-vous qu'environ 78 % des élèves du secondaire à Montréal maîtrisent ce calcul? C'est une base solide pour se lancer dans des carrières passionnantes comme le génie civil ou le design industriel. Pour en savoir plus, vous pouvez consulter l'histoire et l'importance du cylindre.
En reliant la théorie à des objets tangibles, comme une simple boîte de conserve, la formule de l'aire d'un cylindre devient soudainement un outil concret, beaucoup plus facile à mémoriser.
Bien sûr, se souvenir de toutes ces formules peut être un vrai défi. Heureusement, certaines techniques peuvent grandement vous aider. Découvrez comment améliorer sa mémoire pour les études avec nos stratégies éprouvées et facilitez votre parcours d'apprentissage.
Des questions? On y répond!
Même avec la meilleure des formules, il reste parfois quelques petites zones d'ombre. C'est tout à fait normal! Faisons le tour des questions les plus fréquentes pour que le calcul de l'aire d'un cylindre n'ait plus aucun secret pour vous.
Aire ou volume, quelle est la différence?
Imaginez une conserve. Si vous vouliez la peindre, vous auriez besoin de connaître son aire. C'est la surface totale de métal à couvrir, qu'on mesure en centimètres carrés (cm²).
Maintenant, si vous vouliez savoir combien de soupe elle peut contenir, vous calculeriez son volume. C’est l’espace à l’intérieur, mesuré en centimètres cubes (cm³). L'un mesure une surface, l'autre une capacité.
Et si on me donne seulement le diamètre?
C'est un classique des exercices de maths! Pas de panique. Rappelez-vous simplement que le rayon est toujours la moitié du diamètre.
Il suffit donc de diviser le diamètre par 2 pour trouver votre rayon (r = d/2) avant de vous lancer dans la formule de l'aire. Un petit calcul de plus, et le tour est joué.
Et pour un cylindre ouvert, comme un verre? On doit ajuster la formule. On ne calcule qu'une seule base (πr²) et on l'ajoute ensuite à l'aire de la paroi latérale (2πrh).
Il faut aussi savoir que la formule standard s'applique à un cylindre bien droit. S'il est penché (on parle de cylindre oblique), les calculs deviennent un peu plus complexes.
Si ces concepts mathématiques représentent encore un défi pour votre enfant, Centrétudes propose un accompagnement personnalisé pour l'aider à bâtir sa confiance et à maîtriser la matière. Découvrez comment nous pouvons l'aider sur https://centretudes.ca.


