Pourquoi le volume d'un cône vous paraît compliqué (et comment y remédier)

Avouons-le, la formule du volume d'un cône, avec ses π, ses carrés et ses fractions, peut faire peur ! Pourtant, c'est une mesure hyper utile au quotidien. Imaginez : vous préparez des cornets de glace. Connaître le volume vous permet de savoir exactement combien de crème glacée chaque cornet peut contenir. Idem pour remplir un pot de fleurs conique de terreau : vous achetez la bonne quantité, sans gaspillage. Ce concept de volume, qui représente l'espace occupé par un objet en 3D, est d'ailleurs enseigné dans les écoles californiennes, comme partout aux États-Unis. Environ 90% des collégiens californiens étudient la géométrie, y compris les volumes. En savoir plus sur le volume des cônes
Et ce n'est pas si abstrait que ça ! Regardez autour de vous : un abat-jour, un entonnoir, ou même un chapeau pointu… Des cônes, il y en a partout ! Calculer leur volume peut servir dans des situations étonnantes : des projets artistiques, des recettes de cuisine, du bricolage… Un bon conseil : pour bien progresser dans vos études, n'hésitez pas à consulter des ressources qui peuvent vous aider. Découvrez nos conseils pour étudier efficacement.
Par exemple, si vous organisez une fête et que vous avez des petits chapeaux coniques à remplir de bonbons, calculer le volume de chaque chapeau vous évitera d'en acheter trop… ou pas assez ! Les enfants seront contents, et votre porte-monnaie aussi. Alors, prêt à apprivoiser le volume d'un cône ? Vous verrez, c'est plus simple qu'il n'y paraît, et ça peut vraiment vous simplifier la vie.
Décoder la formule V = (1/3) × π × r² × h sans se prendre la tête
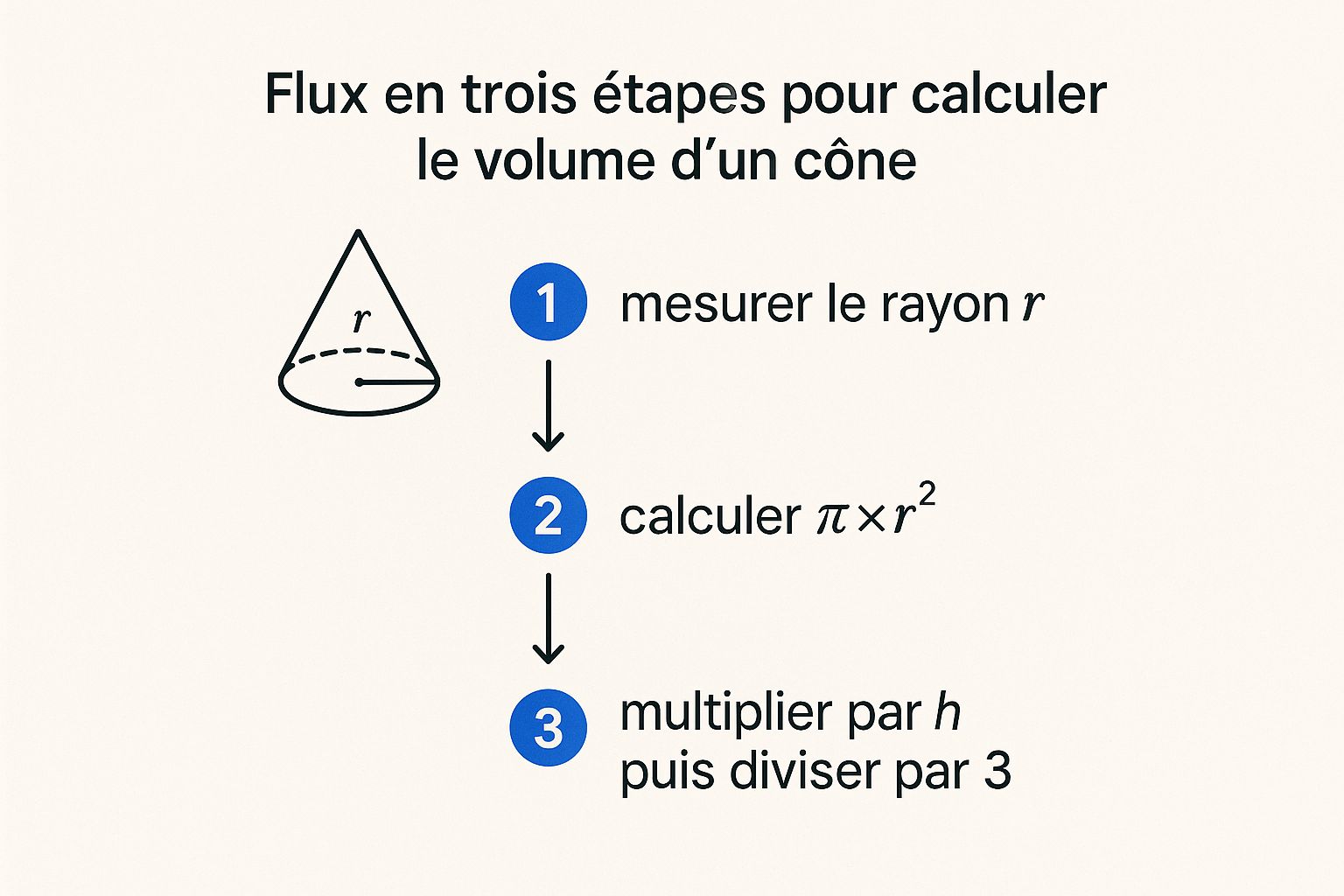
L'infographie illustre bien les étapes pour calculer le volume d'un cône. Rayon, aire de la base, et enfin la hauteur divisée par 3. C'est comme assembler un puzzle, chaque pièce a son importance pour arriver au volume final. On voit bien que l'aire de la base et la hauteur sont les éléments clés pour calculer le volume d'un cône.
La formule V = (1/3) × π × r² × h peut sembler compliquée à première vue, mais croyez-moi, c'est plus simple qu'il n'y paraît. Prenons le rayon (r) : imaginez une pizza, le rayon c'est la distance entre le centre et le bord. Plus le rayon est grand, plus la pizza est grande, n'est-ce pas ?
Le r², c'est simplement le rayon multiplié par lui-même, ce qui nous donne l'aire de la base circulaire. Et π (pi), environ 3,14, c'est la constante magique qui relie le rayon à l'aire du cercle.
La hauteur (h), c'est la distance entre la pointe du cône et sa base. Imaginez une pile de crêpes : plus la pile est haute, plus il y a de crêpes, et plus le cône est haut, plus son volume est important.
Enfin, le 1/3. Figurez-vous qu'un cône occupe exactement un tiers de l'espace d'un cylindre qui aurait la même base et la même hauteur. C'est une relation géométrique fondamentale!
Comparaison des volumes : cône vs autres solides
Pour mieux comprendre la relation entre le volume d'un cône et celui d'autres solides, voici un tableau comparatif. Il met en lumière les liens entre les formules et les coefficients multiplicateurs.
| Solide | Formule du volume | Relation avec le cône | Coefficient multiplicateur |
|---|---|---|---|
| Cône | (1/3) × π × r² × h | – | 1 |
| Cylindre | π × r² × h | 3 fois le volume du cône | 3 |
| Pyramide (base carrée) | (1/3) × côté² × h | Similaire au cône, mais avec une base carrée | Adaptable selon la base |
| Prisme (base carrée) | côté² × h | 3 fois le volume d'une pyramide à base carrée | Adaptable selon la base |
Ce tableau montre bien que le volume du cône est lié à celui d'autres solides. Le coefficient 1/3 est vraiment caractéristique du cône et de la pyramide.
Besoin d'un coup de pouce ? Je vous conseille de jeter un œil aux ressources de tutorat en mathématiques. Retenir la formule, c'est bien, mais la comprendre, c'est la clé !
Identifier le rayon et la hauteur sans se tromper (les pièges classiques)

Croyez-moi, le calcul du volume d'un cône, c'est souvent là que le bât blesse ! L'erreur classique ? Confondre rayon et diamètre. On prend le diamètre entier au lieu de la moitié, et paf ! Un résultat quatre fois trop grand. Je l'ai vu tellement de fois ! Petit rappel : le rayon, c'est la distance du centre du cercle au bord.
Autre piège fréquent : la hauteur. On la confond avec la génératrice, cette ligne inclinée sur le côté. Erreur ! La hauteur, c'est la distance verticale entre la pointe et la base. Imaginez un cornet de glace posé sur une table : la hauteur, c'est la distance entre la table et la pointe du cornet. Le rayon, c'est la moitié du diamètre de l'ouverture.
Astuces pour mesurer
Vous n'avez qu'un mètre ruban ? Pas de panique ! Pour un cône régulier, comme un verre conique, mesurez la circonférence de la base. Divisez cette valeur par 2π (environ 6,28) pour obtenir le diamètre, puis divisez à nouveau par deux pour trouver le rayon.
Et pour la hauteur, si la mesure directe est impossible, placez le cône contre un mur. Mesurez la distance horizontale entre la base et la pointe. Un peu de trigonométrie (ou une application mobile) vous permettra de calculer la hauteur verticale. Un petit coup de pouce pour les devoirs ? Jetez un œil au site du Centre Études, il regorge de ressources utiles.
Bien sûr, certains cônes, comme les cônes irréguliers, sont plus complexes à mesurer. L’important, c’est de bien saisir la différence entre rayon, diamètre, hauteur et génératrice. Avec un peu d'entraînement, calculer le volume d'un cône deviendra un jeu d'enfant !
Calculs concrets avec des objets que vous connaissez
Imaginez un cornet de glace, genre classique : 6 cm de diamètre en haut, 12 cm de haut. Pour le volume, on a besoin du rayon, c'est la moitié du diamètre, donc 3 cm. Et 3² = 9. Avec π ≈ 3,14, la formule du volume nous donne : V = (1/3) × 3,14 × 9 × 12 = 113 cm³ environ. De quoi se régaler !
Maintenant, prenons un chapeau pointu de fête d'anniversaire. Disons 10 cm de diamètre à la base et 15 cm de haut. Rayon ? 5 cm. Donc, le volume : V = (1/3) × 3,14 × 25 × 15 = 393 cm³. Pas mal de place pour des petits cadeaux !
Et pour finir, un entonnoir de cuisine : 8 cm de diamètre, 7 cm de haut. Le volume de ce cône : V = (1/3) × 3,14 × 16 × 7 = 117 cm³ à peu près. Super pratique pour transvaser !
Vous avez remarqué comment je m'y prends ? Je note les mesures, je calcule le carré du rayon, et ensuite je fais la multiplication tranquillement, étape par étape. C’est mon truc pour éviter les erreurs sur la calculatrice. Et puis, ça permet de voir si le résultat est logique par rapport à la taille de l'objet. En parlant de ça, j'ai vu que les élèves californiens sont plutôt bons en maths. Apparemment, en 2022, 70% d'entre eux avaient de bons résultats aux tests au collège. Ça montre que leurs programmes scolaires sont efficaces. Si vous voulez en savoir plus sur le calcul du volume d'un cône, c'est par ici !
Astuces pour des calculs précis
Petit conseil : n'arrondissez pas π trop tôt ! Utilisez 3,14 en général, ou 3,1416 si vous voulez être plus précis. La touche π de votre calculatrice, c’est le top pour la précision. Autre chose : pour vérifier rapidement votre résultat, souvenez-vous que le volume d'un cône est toujours plus petit que celui d'un cylindre avec la même base et la même hauteur.
Outils malins pour calculer plus vite et sans erreur

Oubliez les calculs manuels interminables ! Calculer le volume d'un cône est devenu super simple grâce aux outils modernes. Perso, je suis fan des calculatrices en ligne. Rayon, hauteur, clic, et voilà ! Le résultat apparaît comme par magie. C'est vraiment pratique pour vérifier rapidement ses calculs ou tout simplement gagner du temps. Il existe même des applications mobiles capables de scanner un objet conique pour estimer ses dimensions. D'ailleurs, en Californie, surtout dans la Silicon Valley, l'innovation est partout, même dans le domaine des maths. Des formules comme celle du volume d'un cône sont essentielles pour développer de nouveaux produits. Envie d'en savoir plus sur le cône ?)
Choisir la bonne valeur pour π
Un petit truc concernant π : pour une approximation rapide, 3,14 suffit amplement. Besoin de plus de précision ? Utilisez 3,1416. Et pour une précision absolue, la fonction π de votre calculatrice est votre meilleure alliée. J'ai une petite astuce pour vérifier la cohérence de mes résultats : le volume d'un cône est toujours inférieur à celui d'un cylindre avec la même base et la même hauteur. Si ce n'est pas le cas, il y a forcément une erreur ! Besoin d'un coup de pouce pour vos devoirs ? Jetez un œil au site de Centrétudes pour du tutorat et de l'aide aux devoirs en ligne.
Organiser ses calculs
Dernier conseil, et pas des moindres : organisez vos calculs. Notez d'abord le rayon et la hauteur. Calculez ensuite le carré du rayon (r²). Multipliez le résultat par π et par la hauteur. Enfin, divisez par 3. Simple, mais efficace pour éviter les erreurs de frappe, surtout sur la calculatrice.
Pour vous aider à choisir l'outil le plus adapté à vos besoins, voici un tableau comparatif :
Avant de se lancer tête baissée dans les calculs, il est utile de comparer les différents outils disponibles. Le tableau ci-dessous résume les avantages et les inconvénients de chacun.
| Outil | Facilité d'utilisation | Précision | Disponibilité | Fonctionnalités bonus |
|---|---|---|---|---|
| Calculatrice scientifique | Moyenne | Élevée (dépend de la valeur de π utilisée) | Largement disponible | Fonctions trigonométriques, etc. |
| Calculatrice en ligne | Facile | Variable (vérifier la précision de π utilisée) | Nécessite une connexion internet | Souvent couplée à une visualisation du cône |
| Application mobile | Facile (surtout avec scan) | Variable (dépend de la méthode d'estimation) | Nécessite un smartphone/tablette | Possibilité de scanner des objets réels |
| Calcul manuel | Difficile (risque d'erreur) | Élevée (dépend de la valeur de π utilisée) | Toujours disponible | Développe la compréhension des formules |
Comme vous pouvez le constater, chaque outil a ses points forts et ses points faibles. Le choix dépendra de vos besoins en termes de précision, de rapidité et d'accessibilité.
Avec ces quelques astuces, vous êtes parés pour calculer le volume d'un cône avec précision et rapidité, que ce soit pour un devoir ou pour un projet personnel.
Applications surprenantes dans vos projets quotidiens
Figurez-vous que calculer le volume d'un cône peut vous dépanner plus souvent qu'on ne le pense ! Par exemple, en pâtisserie, c'est devenu mon astuce secrète pour doser parfaitement la ganache dans mes moules coniques. Adieu le gaspillage et les cornets à moitié vides ! Et pour un projet déco, ça m'a permis de commander la juste quantité de sable coloré pour remplir mes vases coniques. Pratique, non ?
Mais attendez, ce n'est pas tout ! Au jardin, cette formule est super utile pour bien dimensionner un système d'arrosage avec des réservoirs coniques. Un ami sculpteur s'en sert même pour estimer la quantité d'argile dont il a besoin. Besoin de faire le point sur l'actualité ? Apprenez à créer une revue de presse efficace. Et même en cuisine, si vous voulez épater vos invités avec des présentations originales en forme de cône, calculer le volume vous aidera à prévoir les portions.
Des exemples concrets
-
Des verrines parfaites: Imaginez de jolies verrines en forme de cône pour un dessert raffiné. Calculer le volume vous assure d'avoir la quantité idéale de mousse ou de crème, sans gaspillage et avec une présentation impeccable.
-
Des projets créatifs réussis: Si vous vous lancez dans la fabrication d'objets déco en béton, par exemple des bougeoirs coniques, le calcul du volume vous permettra d'acheter la quantité exacte de béton. Plus de gâchis, et un budget maîtrisé !
-
Du jardinage précis: Vous avez un joli pot conique à remplir de terreau ? Hop, un petit calcul de volume et vous savez exactement combien en acheter. Fini les sacs de terreau en trop qui s'entassent au fond du garage !
Adapter la théorie à la pratique
Le secret, c'est d'adapter la formule à la réalité du terrain. Si votre cône n'est pas parfaitement régulier, prenez des mesures à plusieurs endroits et faites une moyenne. Une petite marge de sécurité ne fait jamais de mal non plus ! Vous pourriez aussi être intéressé par ce guide sur le tutorat en sciences. Et n'oubliez pas : des mesures précises, c'est la base d'un calcul de volume fiable.
Besoin d'un coup de pouce pour les études, pour vous ou vos enfants ? Centrétudes, notre centre de tutorat à Montréal, propose un accompagnement personnalisé du primaire au collégial. Maths, français, anglais, sciences… Nos tuteurs sont là pour aider vos enfants à réussir. Découvrez nos services sur notre site web et offrez à votre enfant le soutien scolaire dont il a besoin.


