La formule du volume d'un cône est un outil mathématique incontournable qui se résume en une expression assez simple : V = (1/3)πr²h.
Cette formule vous permet de calculer l'espace à l'intérieur de n'importe quel cône, que ce soit un simple cornet de crème glacée ou un tas de sable dans une cour. Le petit détail qui change tout, c'est ce fameux facteur (1/3). Il marque la différence fondamentale entre le volume d'un cône et celui d'un cylindre.
Déchiffrer la formule du volume d'un cône

Plongeons au cœur de cette formule pour voir ce que chaque symbole veut vraiment dire. Loin d'être une suite de lettres abstraites, chaque variable représente une dimension bien réelle de l'objet. Comprendre ces composantes, c'est la première étape pour utiliser la formule sans hésiter.
Imaginez un cylindre et un cône qui ont exactement la même base circulaire et la même hauteur. Si vous remplissiez le cône d'eau pour le verser dans le cylindre, il vous faudrait le faire trois fois pour remplir le cylindre au complet. C'est l'idée derrière le « 1/3 » de la formule. Simple, non?
Les composantes essentielles de la formule
Pour bien saisir le rôle de chaque élément de la formule V = (1/3)πr²h, ce tableau décompose chaque variable et constante pour une compréhension claire et rapide.
| Symbole | Signification | Description |
|---|---|---|
| V | Volume | C'est l'espace total à l'intérieur du cône, ce que l'on cherche à trouver. L'unité est toujours cubique (cm³, m³). |
| π | Pi | La célèbre constante mathématique, qu'on arrondit souvent à 3,14159. Elle est cruciale pour tout calcul lié aux cercles. |
| r | Rayon | C'est la distance entre le centre de la base circulaire du cône et son pourtour. Attention à ne pas la confondre avec le diamètre! |
| h | Hauteur | Il s'agit de la distance verticale, bien droite, entre la pointe du cône (l'apex) et le centre de sa base. |
Cette décomposition rend le calcul beaucoup plus facile à aborder. En comprenant bien le rôle de chaque élément, vous vous assurez une base solide pour la suite.
D'ailleurs, si vous cherchez à améliorer votre manière de travailler en général, découvrir comment étudier efficacement pourrait complètement transformer votre approche des maths et des autres matières.
La logique fascinante derrière la formule
La formule du volume d'un cône ne sort pas d’un chapeau de magicien! Elle découle d’une logique visuelle et mathématique qui remonte à l’Antiquité, notamment aux travaux du brillant Archimède. Mais rassurez-vous, pas besoin de décoder de vieux parchemins pour en comprendre l’essence.
Pour percer le mystère du fameux « 1/3 », imaginez une expérience toute simple. Prenez un cylindre et un cône qui ont une base et une hauteur parfaitement identiques. Si vous remplissez le cône de sable ou d’eau pour le verser dans le cylindre, vous constaterez qu’il faut le faire trois fois pour remplir complètement le cylindre.
Cette relation physique toute simple est la clé! Le volume du cône est directement lié à celui du cylindre. La formule du volume d’un cylindre étant πr²h, et comme le cône n’occupe qu’un tiers de cet espace, sa formule devient logiquement (1/3)πr²h.
Une histoire d'empilement infini
Une autre façon de visualiser d'où vient cette formule s'inspire d'une méthode appelée le principe de Cavalieri. Imaginez que votre cône est une pile de disques, un peu comme une tour de crêpes où chaque nouvelle crêpe est un peu plus petite que la précédente.
- Le disque du bas : C’est la base du cône, avec une aire de πr².
- Les disques du milieu : En montant vers le sommet, le rayon de chaque disque diminue petit à petit.
- Le disque du sommet : Tout en haut, le dernier disque est infiniment petit, un simple point qu'on appelle l'apex.
C’est en additionnant le volume de cette infinité de disques de plus en plus fins que les mathématiciens ont démontré que le total équivaut précisément au tiers du volume d'un cylindre de mêmes dimensions. Bien que la démonstration mathématique soit complexe, l'idée de cet empilement rend le concept beaucoup plus intuitif.
La formule V = (1/3)πr²h n'est donc pas une règle arbitraire à mémoriser bêtement. C'est la conclusion logique de la géométrie même du cône, une vérité mathématique élégante qui montre comment une forme pointue remplit l’espace.
Comprendre cette logique transforme une formule qui peut sembler abstraite en un concept concret et facile à retenir. Avoir des bases solides comme celle-ci est essentiel pour aborder les maths avec confiance. D'ailleurs, c'est une des 5 bonnes raisons d'opter pour le tutorat dès le début de l'année scolaire afin de bien cimenter sa compréhension.
Appliquer la formule étape par étape sans se tromper
La théorie, c'est bien, mais la pratique, c'est encore mieux. Maîtriser la formule du volume d'un cône signifie surtout savoir l'appliquer avec confiance et précision. Ce guide pratique décompose le calcul en cinq étapes simples et logiques pour vous mener au bon résultat, à chaque fois.
Passer à l'action est la meilleure façon de consolider ses connaissances. En suivant cette méthode, vous éviterez les erreurs classiques et vous développerez de bons réflexes pour tous vos futurs problèmes de géométrie.
L'infographie suivante illustre bien comment la formule du volume du cône découle logiquement de celle du cylindre, en mettant en lumière l'étape cruciale de la division par trois.
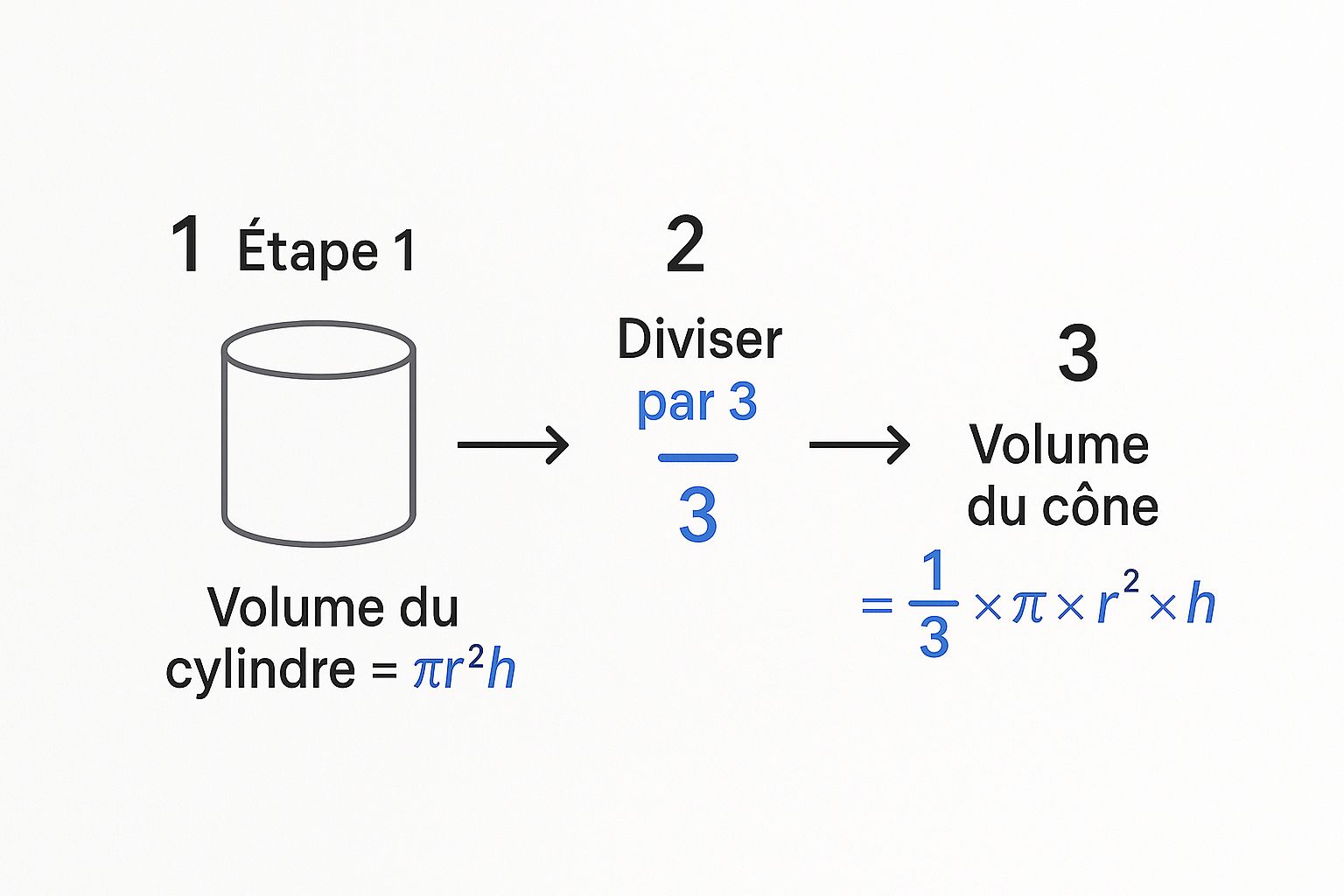
Ce schéma montre clairement que le volume d'un cône est simplement le tiers du volume du cylindre qui pourrait le contenir. C'est une astuce visuelle puissante pour ne jamais oublier ce fameux « 1/3 ».
La méthode infaillible en 5 étapes
Pour trouver le volume d’un cône avec la formule V = (1/3)πr²h, il suffit de suivre cette séquence dans l’ordre. Chaque étape est pensée pour réduire au minimum les risques d’erreur.
- Trouver le rayon (r) : C'est le point de départ. Identifiez le rayon de la base circulaire. Si l’énoncé vous donne le diamètre, n'oubliez pas de le diviser par deux pour obtenir le rayon. Ne sautez jamais cette vérification!
- Mettre le rayon au carré (r²) : Une fois le rayon en main, multipliez-le par lui-même. Omettre cette étape est une erreur fréquente qui faussera complètement le résultat final.
- Multiplier par la hauteur (h) : Multipliez le résultat précédent (r²) par la hauteur du cône. Faites bien attention d'utiliser la hauteur perpendiculaire (la ligne droite du sommet au centre de la base), et non la génératrice (la longueur de la pente).
- Multiplier par Pi (π) : Prenez le nombre obtenu et multipliez-le par π. Pour la plupart des exercices scolaires, utiliser une approximation comme 3,14159 ou simplement conserver le symbole π dans la réponse est accepté.
- Diviser le tout par 3 : C'est l'étape finale et décisive. Divisez le résultat total par 3 (ou, ce qui revient au même, multipliez par 1/3). C'est ce qui distingue le volume du cône de celui du cylindre.
N'oubliez jamais les unités! Si vos mesures de départ sont en centimètres (cm), votre volume final devra être exprimé en centimètres cubiques (cm³). C'est un détail qui fait toute la différence sur une copie d'examen.
Astuces pour un calcul sans faute
Au-delà des étapes, quelques bonnes habitudes peuvent vous sauver la mise. Avant de vous lancer dans les calculs, prenez un instant pour visualiser le cône et bien identifier chaque mesure.
Dessiner un petit schéma rapide est souvent une excellente idée. Ça vous aide à ne pas mélanger la hauteur, le rayon et la génératrice, ce qui évite bien des confusions.
Pour aller plus loin et voir des exemples concrets, notre guide complet sur le calcul du volume d'un cône vous propose des exercices corrigés et des explications supplémentaires. C'est une ressource parfaite pour vous entraîner. Finalement, prenez l'habitude de toujours vérifier votre calcul, idéalement en le refaisant dans un ordre différent pour confirmer le résultat.
Le volume du cône dans notre quotidien
La formule du volume d'un cône n’est pas qu’une simple ligne dans un manuel de mathématiques; c’est une clé qui nous permet de mieux comprendre et de quantifier le monde qui nous entoure. La forme conique est partout, des objets de tous les jours aux phénomènes naturels. Comprendre son volume, c’est donc mieux apprécier notre environnement et interagir avec lui.
Cette formule mathématique est bien plus concrète qu’on ne pourrait le croire. Elle se cache dans des situations variées, parfois amusantes, souvent très pratiques. Chaque fois que vous croisez un objet qui s’élargit à partir d’une pointe, sachez que la formule V = (1/3)πr²h est à l'œuvre.
Exemples concrets où le volume du cône compte
Pensez à votre prochaine visite au cinéma ou à la fête foraine. Le cornet de maïs soufflé que vous tenez dans vos mains est un cône parfait! Sa capacité n'est pas un mystère; elle peut être calculée avec une grande précision. Un cornet avec un rayon de 8 cm et une hauteur de 20 cm peut contenir environ 1 340 cm³ de friandises!
Prenons un autre exemple : le porte-filtre à café de forme conique, un classique dans bien des cuisines. Le volume de café qui peut s'y écouler dépend directement de ses dimensions. Un petit changement dans le rayon ou la hauteur du filtre et c'est toute la quantité de café que vous pouvez préparer qui est modifiée. Voilà un bel exemple de l’impact de chaque variable de la formule.
La beauté de la formule du volume du cône réside dans sa capacité à traduire des formes physiques en chiffres concrets. Elle nous donne le pouvoir de mesurer, de comparer et d'optimiser, que ce soit pour une recette de cuisine ou un projet de construction.
Ces applications pratiques ne se limitent pas à la nourriture. Dans le domaine de la construction, un tas de sable ou de gravier prend souvent la forme naturelle d'un cône. Les ingénieurs et les chefs de chantier utilisent cette formule pour estimer rapidement la quantité de matériaux disponible sur un site, un calcul essentiel pour la logistique et la gestion des coûts. Cette compétence à décrire des scènes complexes est d'ailleurs une des bases pour maîtriser les différents types de textes en français.
L'impact des dimensions sur le volume
Il est fascinant de voir à quel point de petits changements dans le rayon ou la hauteur peuvent radicalement modifier le volume d'un cône. Comme le rayon est mis au carré (r²) dans la formule, son influence est particulièrement puissante.
Pour mieux visualiser cet effet, analysons quelques scénarios :
- Scénario A (Petit cornet) : Un cône avec un rayon de 5 cm et une hauteur de 15 cm.
- Scénario B (Cornet plus large) : Un cône de même hauteur (15 cm), mais avec un rayon doublé à 10 cm.
Le volume du Scénario A est d'environ 393 cm³. En doublant simplement le rayon dans le Scénario B, le volume explose pour atteindre environ 1 571 cm³. C'est quatre fois plus grand, pas seulement deux fois! Cette relation non linéaire est cruciale à comprendre.
Le tableau suivant illustre clairement comment le rayon et la hauteur influencent le résultat final.
Comparaison du volume pour différents types de cônes
Ce tableau illustre comment des changements dans le rayon et la hauteur affectent de manière significative le volume final du cône.
| Scénario | Rayon (r) | Hauteur (h) | Volume calculé (V) |
|---|---|---|---|
| Cône de base | 6 cm | 10 cm | ≈ 377 cm³ |
| Rayon doublé | 12 cm | 10 cm | ≈ 1 508 cm³ (x4) |
| Hauteur doublée | 6 cm | 20 cm | ≈ 754 cm³ (x2) |
Comme on peut le voir, doubler le rayon a un effet beaucoup plus spectaculaire que de doubler la hauteur.
Ces exemples du monde réel ancrent la formule du volume du cône dans la pratique. Savoir la manipuler n'est pas seulement un exercice scolaire; c'est une compétence analytique utile dans de nombreuses situations, du quotidien à des contextes plus professionnels.
Les 4 erreurs les plus courantes (et comment les éviter)

Même avec une formule aussi simple que V = (1/3)πr²h, de petites erreurs d'inattention peuvent vite se glisser dans vos calculs et fausser complètement votre réponse. La bonne nouvelle, c'est que connaître ces pièges est le meilleur moyen de ne pas tomber dedans. Voyez cette section comme un filet de sécurité pour que vos calculs de volume soient toujours justes.
En analysant les gaffes les plus fréquentes, vous allez développer une routine de vérification simple mais très efficace. Maîtriser ces quelques points vous assurera des résultats corrects à chaque fois et renforcera votre confiance en vos compétences.
Erreur 1: Confondre le rayon et le diamètre
C’est de loin l’erreur la plus commune. Un problème vous donnera souvent le diamètre (la largeur totale de la base) plutôt que le rayon. Si vous utilisez cette valeur directement dans la formule du volume du cône, votre résultat final sera quatre fois trop grand!
Comment l’éviter : Prenez toujours un instant pour vérifier la mesure fournie. Si c'est le diamètre (d), votre toute première étape, avant quoi que ce soit d'autre, doit être de le diviser par deux pour trouver le rayon (r = d/2). Faites-en un réflexe systématique.
Erreur 2: Omettre de mettre le rayon au carré
Dans le feu de l'action, le petit « ² » à côté du « r » dans la formule (r²) est facile à oublier. Pourtant, son impact est énorme. Si vous sautez cette étape, vous calculez le volume d’une forme qui, géométriquement parlant, n'est plus un cône.
La mise au carré du rayon donne son véritable « poids » à la dimension de la base. L'ignorer, c'est sous-estimer radicalement l'impact de la largeur du cône sur son volume total.
Comment l’éviter : Quand vous appliquez la formule, traitez le calcul de r² comme une étape à part entière. Calculez r x r tout de suite après avoir identifié le rayon. Ensuite seulement, utilisez ce nouveau résultat pour la suite des opérations.
Erreur 3: Se tromper de hauteur
Attention, un cône possède deux mesures qui ressemblent à une hauteur : la hauteur verticale (h) et la génératrice (g), parfois appelée apothème ou hauteur oblique. La génératrice, c'est la longueur de la pente, de la pointe du cône jusqu'au bord de sa base.
- Hauteur (h) : C'est la ligne droite et perpendiculaire qui part du sommet et rejoint le centre de la base. C'est celle-ci que vous devez utiliser.
- Génératrice (g) : C'est la ligne inclinée sur le côté du cône. Elle est toujours plus longue que la hauteur.
Comment l’éviter : Faites un petit croquis rapide pour bien visualiser le cône. La hauteur forme toujours un angle droit avec le rayon. Si on vous donne la génératrice, il faudra sûrement utiliser le théorème de Pythagore (h² + r² = g²) pour trouver la vraie hauteur h. D'ailleurs, de bonnes bases en géométrie sont un atout majeur, même pour des épreuves où l'on s'y attend moins, comme pour réussir son examen de français au secondaire, où la logique est aussi très importante.
Erreur 4: Oublier la division par trois
Ne pas diviser le résultat final par trois est une erreur classique. Mathématiquement, cela revient à transformer votre cône en cylindre. Vous obtiendrez alors un volume exactement trois fois supérieur à la bonne réponse.
Comment l’éviter : Pensez à la division par trois comme l'étape finale, la signature même du cône. Une fois que vous avez le résultat de π x r² x h, arrêtez-vous un instant et demandez-vous : « Est-ce que j'ai bien divisé par trois? » Cette dernière vérification vous sauvera la mise plus d'une fois.
Mettez vos connaissances à l'épreuve avec quelques exercices
La théorie, c'est bien, mais c'est en pratiquant qu'on devient vraiment bon. Rien ne vaut de mettre la main à la pâte pour que la formule du volume du cône devienne un vrai réflexe. Cette section a été pensée pour vous permettre de tester ce que vous venez d'apprendre, étape par étape.
On va y aller doucement, en commençant par des problèmes simples avant d’augmenter un peu le niveau de difficulté. L'idée, ce n'est pas de vous piéger, mais de bâtir votre confiance. Vous verrez que vous êtes tout à fait capable de jongler avec la formule dans différentes situations. C'est le moment de passer de la théorie à la pratique!
Exercice 1 : Le calcul de base
On commence avec le scénario le plus direct, parfait pour s’échauffer. L'objectif est d'appliquer la formule V = (1/3)πr²h sans flafla.
Problème : Un cône de signalisation a un rayon de base de 15 cm et une hauteur de 50 cm. Quel est son volume? (On prendra π ≈ 3,14159)
-
Correction détaillée :
- On sort les données : r = 15 cm et h = 50 cm.
- On met le rayon au carré : r² = 15² = 225 cm².
- On multiplie par la hauteur et Pi : 225 × 50 × 3,14159 ≈ 35 342,875.
- On divise le tout par 3 : 35 342,875 ÷ 3 ≈ 11 780,96 cm³.
Le volume du cône de signalisation est donc d'environ 11 781 cm³.
Exercice 2 : Trouver le rayon à partir du diamètre
Cet exercice ajoute une petite étape qu'on rencontre tout le temps : passer du diamètre au rayon. C'est un excellent test pour s'assurer de ne pas tomber dans l'un des pièges les plus courants.
Problème : Un cornet de crème glacée a une hauteur de 12 cm et un diamètre d'ouverture de 6 cm. Quel volume de crème glacée peut-il contenir s'il est rempli parfaitement à ras bord?
Rappelez-vous, la formule a besoin du rayon, pas du diamètre! Cette première étape de conversion est essentielle pour obtenir la bonne réponse. C'est un réflexe à prendre pour tous les problèmes de géométrie qui impliquent des cercles.
-
Correction détaillée :
- On trouve le rayon : Le diamètre est de 6 cm, donc le rayon (r) est tout simplement 6 ÷ 2 = 3 cm.
- On applique la formule : V = (1/3) × π × (3)² × 12.
- On calcule : V = (1/3) × π × 9 × 12 = 4 × 9 × π = 36π.
- On obtient le résultat numérique : 36 × 3,14159 ≈ 113,1 cm³.
Le cornet peut donc contenir environ 113 cm³ de crème glacée.
Exercice 3 : À la recherche d'une dimension manquante
Maintenant, on inverse le problème. On vous donne le volume, mais il manque une des mesures. Cet exercice demande un peu d'algèbre de base pour isoler la variable qu'on cherche.
Problème : Un tas de sable en forme de cône a un volume de 200 m³. Le rayon de sa base mesure 5 m. Quelle est sa hauteur?
-
Correction détaillée :
- On pose l'équation avec ce qu'on sait : 200 = (1/3) × π × 5² × h.
- On simplifie un peu : 200 = (1/3) × π × 25 × h.
- On se débarrasse de la division par 3 en multipliant : 600 = 25πh.
- On isole h : h = 600 ÷ (25π).
- On calcule le résultat final : h ≈ 600 ÷ (78,54) ≈ 7,64 m.
La hauteur du tas de sable est d'environ 7,64 mètres.
En mathématiques, la pratique régulière est vraiment la clé du succès. Si ces exercices vous ont paru un peu ardus ou si vous voulez simplement aiguiser vos compétences avec un coup de pouce personnalisé, Centrétudes est là pour vous aider. Nos tuteurs spécialisés peuvent vous guider pas à pas pour que chaque formule devienne un outil que vous maîtrisez en toute confiance. Découvrez nos services de tutorat en mathématiques.


