Le calcul du volume d'un cône est bien plus intuitif qu'on pourrait le penser. Tout se résume à une formule mathématique simple et élégante : V = (1/3)πr²h. Grâce à cette équation, vous pouvez déterminer l'espace occupé par n'importe quel objet de forme conique, que ce soit un simple cornet de crème glacée ou un cône de signalisation.

Plonger dans la géométrie du cône
Avant même de mémoriser la formule, il est essentiel de bien se représenter ce qu'est un cône et de comprendre les éléments qui le définissent. Pensez aux objets qui vous entourent : un chapeau de fête, un entonnoir, ou même un volcan. Tous partagent cette forme géométrique fascinante.
Savoir calculer le volume d'un cône n'est pas qu'un simple exercice scolaire. Cette compétence trouve des applications très concrètes dans plusieurs domaines. Un ingénieur pourrait s'en servir pour estimer la capacité d'un silo à grains, tandis qu'un pâtissier l'utiliserait pour doser précisément ses ingrédients à l'aide d'une poche à douille.
Les composantes de la formule
Ce qui est formidable avec la formule du volume d'un cône, c'est sa simplicité. Elle ne repose que sur deux mesures fondamentales : le rayon de sa base et sa hauteur.
Pour mieux visualiser, décomposons chaque élément.
Les éléments clés de la formule du volume
Ce tableau décompose chaque variable de la formule pour une compréhension immédiate.
| Symbole | Signification | Son rôle dans le calcul |
|---|---|---|
| V | Volume | C’est le résultat que l’on cherche : l’espace total à l’intérieur du cône. |
| π (Pi) | Constante (≈ 3,14159) | Un nombre essentiel pour tout ce qui est circulaire, comme la base du cône. |
| r | Rayon de la base | Détermine la largeur de la base circulaire. Son impact est grand, car il est au carré. |
| h | Hauteur | Mesure la distance verticale du sommet à la base. Elle définit l'étirement du cône. |
Chaque symbole a donc une mission claire et contribue directement au résultat final.
Il y a un piège à éviter : ne confondez jamais la hauteur (h) avec l'apothème (aussi appelée génératrice), qui correspond à la longueur de la pente du cône. Pour le volume, seule la hauteur verticale, perpendiculaire à la base, nous intéresse.
Cette introduction vous donne les bases pour attaquer le calcul avec assurance. Si certains concepts mathématiques vous semblent encore un peu flous, un accompagnement personnalisé peut vraiment faire la différence. Pour trouver un soutien scolaire adapté, jetez un œil aux services de tutorat offerts par Centrétudes.
Dans les sections qui suivent, nous allons décortiquer la logique derrière cette formule et voir comment l'appliquer, étape par étape, avec des exemples clairs.
La logique derrière la formule V = (1/3)πr²h
À première vue, la formule du volume d'un cône, V = (1/3)πr²h, peut sembler un peu intimidante. Pourtant, chaque symbole raconte une partie de l'histoire. Une fois décodée, elle devient incroyablement logique et même facile à retenir.
Décortiquons-la ensemble pour qu'elle n'ait plus aucun secret pour vous.
Imaginez que vous construisiez un cône en empilant des disques de carton, un peu comme des rondelles, les uns sur les autres. Vous commenceriez par un grand disque pour la base, puis vous ajouteriez des disques de plus en plus petits jusqu'à atteindre la pointe. Cette image toute simple nous aide à comprendre les deux éléments clés de la formule : la surface de la base et la hauteur.
Le rôle de la base et de la hauteur
La première partie de l'équation, πr², vous dit probablement quelque chose. C'est la formule pour calculer l'aire d'un cercle, qui correspond ici à la base de notre cône. Le rayon (r) définit la largeur de cette base, et le fameux nombre Pi (π) est essentiel pour tout ce qui touche aux cercles.
Ensuite, nous avons la hauteur (h). Elle représente la distance bien droite entre le centre de la base et le sommet du cône. La hauteur détermine à quel point le cône est « étiré » vers le haut. Si on s'arrêtait là et qu'on multipliait simplement l'aire de la base (πr²) par la hauteur (h), on obtiendrait le volume d'un cylindre. Mais un cône, ce n'est pas un cylindre, c'est plus petit. C'est ici qu'intervient le facteur le plus curieux.
Cette infographie montre bien comment chaque élément de la formule contribue au résultat final.
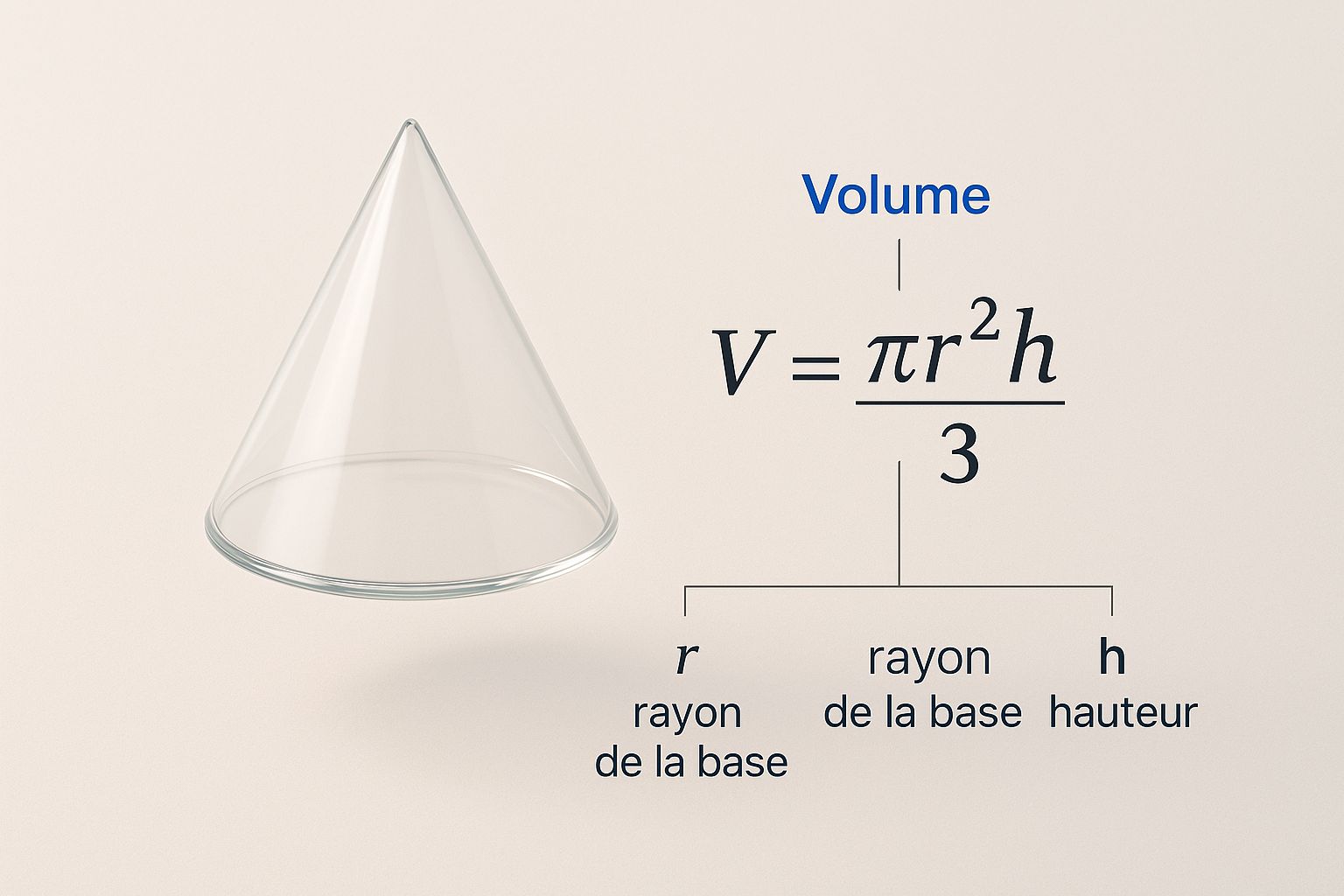
L'image met en évidence la relation directe entre les dimensions du cône (son rayon et sa hauteur) et le calcul final de son volume.
Le mystère du facteur 1/3
Alors, pourquoi doit-on diviser par trois, ou multiplier par 1/3? C'est la clé pour comprendre la différence de volume entre un cône et un cylindre.
Imaginez un cylindre et un cône qui partagent exactement la même base circulaire et la même hauteur. Si vous remplissiez le cône de sable ou d'eau, il vous faudrait le vider exactement trois fois dans le cylindre pour le remplir au complet.
Cette relation de 1 pour 3 est une propriété géométrique fondamentale. Le volume d'un cône est précisément un tiers du volume du cylindre qui pourrait le contenir. Ce n'est pas une approximation, mais bien un fait mathématique prouvé.
Ainsi, la formule V = (1/3)πr²h peut se lire comme une recette en trois étapes simples :
- Calculez l'aire de la base circulaire (πr²).
- Multipliez cette aire par la hauteur (h) pour trouver le volume du cylindre équivalent.
- Divisez ce résultat par 3 pour obtenir le vrai volume du cône.
Cette approche transforme une équation qui semblait abstraite en une logique visuelle et très concrète. Pour explorer davantage cette formule et d'autres concepts, n'hésitez pas à consulter notre guide complet sur le volume d'un cône, qui propose encore plus d'exemples et d'explications détaillées.
D'où vient vraiment la formule du volume
La formule du volume d'un cône, V = (1/3)πr²h, est à la fois élégante et diablement efficace. Mais vous êtes-vous déjà demandé d'où sort ce fameux facteur 1/3? Ce n'est pas un chiffre choisi au hasard; il est le fruit d'un raisonnement mathématique aussi fascinant que rigoureux.

Pour le comprendre, on va faire un petit voyage dans le monde de l'infiniment petit, mais sans se perdre dans des équations compliquées. L'idée de base est de voir le cône non pas comme un tout, mais comme une pile d'une infinité de disques minuscules.
Une construction tranche par tranche
Imaginez un cône, bien stable sur sa base. Maintenant, visualisez qu'on le découpe en une multitude de « tranches » horizontales extrêmement fines. Chaque tranche est en fait un cylindre très, très plat, presque un simple disque.
Le volume total du cône serait donc la somme des volumes de tous ces micro-cylindres empilés les uns sur les autres. C'est le principe fondamental derrière une branche puissante des mathématiques, le calcul intégral : on additionne une infinité de petites parties pour trouver le tout.
Le disque à la base du cône est le plus large, avec un rayon r. À mesure qu'on monte vers le sommet, le rayon de chaque nouvelle tranche diminue progressivement, jusqu'à devenir nul tout en haut. La hauteur h du cône, elle, ne fait que déterminer la hauteur totale de cette pile de disques.
La magie du facteur 1/3
Le lien entre le rayon de chaque disque et sa position en hauteur dans le cône n'est pas dû au hasard; il est linéaire. Cela signifie que la surface des disques diminue en suivant une courbe bien précise. Et lorsqu'on utilise les outils du calcul pour additionner les volumes de toutes ces tranches infiniment fines, de la base jusqu'au sommet, un facteur ressort systématiquement : 1/3.
La formule V = (1/3)πr²h n'est donc ni une approximation ni une simple règle à apprendre par cœur. C'est la conclusion logique du fait qu'un cône est une collection de cercles dont la surface varie d'une manière spécifique avec la hauteur. L'intégration de cette variation mène inévitablement au facteur 1/3.
Ce concept est au cœur de nombreux parcours scientifiques. Par exemple, la notion de volume d'un cône est fondamentale dans les programmes de mathématiques de haut niveau. Dans la région Provence-Alpes-Côte d'Azur, Aix-Marseille Université propose l'un des meilleurs masters en mathématiques appliquées, où les étudiants approfondissent le calcul du volume de solides complexes comme celui-ci. Pour en savoir plus, vous pouvez consulter le classement Thotis des masters en mathématiques.
Cette démonstration, même simplifiée, montre que la formule est le résultat d'une logique implacable. Comprendre d'où elle vient ne fait pas que renforcer vos connaissances; ça transforme une équation abstraite en une vérité tangible et pleine d'élégance.
Mettre la formule en pratique avec des exemples
La théorie, c’est bien, mais rien ne vaut la pratique pour que les concepts prennent vraiment vie. Passer de l'équation abstraite V = (1/3)πr²h à un résultat concret est la meilleure façon de solidifier sa compréhension du volume d'un cône.
Alors, mettons les mains à la pâte. Commençons par un exemple simple pour bien décortiquer chaque étape. Cette approche vous donnera la confiance nécessaire pour vous attaquer ensuite à des problèmes un peu plus corsés.
Exemple 1 : Calculer le volume d’un cône simple
Imaginez un simple cône de signalisation en plastique. On veut savoir quel espace il occupe. Pour ça, il nous faut deux mesures clés : son rayon et sa hauteur.
Disons que notre cône a les dimensions suivantes :
- Rayon (r) : 15 centimètres (cm)
- Hauteur (h) : 40 centimètres (cm)
Maintenant, il suffit d’appliquer la formule : V = (1/3)πr²h.
-
Calculer l’aire de la base (πr²) : On commence par mettre le rayon au carré. Facile.
15² = 225.
Ensuite, on multiplie ce résultat par π (en utilisant une approximation comme 3,14159) :
225 × 3,14159 ≈ 706,86 cm². -
Multiplier par la hauteur (h) : On prend l’aire de la base qu’on vient de trouver et on la multiplie par la hauteur du cône.
706,86 cm² × 40 cm = 28 274,4 cm³. -
Diviser par 3 : C’est l’étape finale, celle qui distingue le cône du cylindre.
28 274,4 cm³ / 3 = 9 424,8 cm³.
Le volume de notre cône de signalisation est donc de 9 424,8 centimètres cubes. Voilà l'espace total à l'intérieur de cet objet.
Exemple 2 : Résoudre un problème à l’envers
Parfois, le défi est un peu différent. Imaginons que vous ayez un verre à cocktail de forme conique. Vous connaissez son volume, mais pas sa hauteur. C'est ce qu'on appelle un problème inverse.
Supposons que le verre peut contenir 200 millilitres (ml) de liquide, ce qui équivaut à 200 cm³. Le rayon de son ouverture est de 5 cm. Alors, quelle est sa hauteur?
On repart de la même formule, mais cette fois, on doit l'isoler pour trouver notre inconnue, « h ».
V = (1/3)πr²h devient h = (3 × V) / (πr²)
Appliquons cette nouvelle équation, étape par étape :
- Calculer (3 × V) : 3 × 200 cm³ = 600 cm³.
- Calculer (πr²) : 5² = 25. Puis, 25 × 3,14159 ≈ 78,54 cm².
- Diviser les résultats : h = 600 cm³ / 78,54 cm² ≈ 7,64 cm.
La hauteur de notre verre à cocktail est donc d’environ 7,64 cm. Savoir manipuler la formule de cette façon est une compétence très utile, que ce soit en classe ou pour des applications bien réelles.
D’ailleurs, la maîtrise de ces concepts géométriques est encouragée bien au-delà des cours traditionnels. Le volume d'un cône est un incontournable des programmes pédagogiques des écoles et universités, comme celles de la région Centre-Val de Loire qui proposent des cursus en statistiques et en ingénierie. La région va même jusqu'à organiser des compétitions où les étudiants appliquent ces notions. Pour en savoir plus, vous pouvez consulter les informations de l'académie d'Orléans-Tours.
Les applications surprenantes du volume du cône
On pense souvent que la formule du volume d'un cône est juste un autre concept appris en classe de mathématiques, destiné à être oublié. Pourtant, cette équation toute simple est un outil redoutable que bien des professionnels utilisent pour résoudre des problèmes très concrets, parfois de manière inattendue.
Loin d'être une simple notion abstraite, cette connaissance géométrique devient une solution pratique dans le monde qui nous entoure. Elle nous aide à quantifier, modéliser et optimiser des objets et des phénomènes de notre quotidien.
De l'ingénierie à la géologie
En ingénierie civile, par exemple, le calcul du volume d’un cône est une compétence de base. Les ingénieurs s’en servent pour évaluer la quantité de matériaux comme le sable, le gravier ou le sel de déneigement, qui sont souvent stockés en grands tas coniques. Une estimation juste est cruciale pour bien gérer les stocks et planifier la logistique.
Dans un tout autre domaine, les géologues utilisent ce même calcul pour comprendre des formations naturelles. Ils peuvent ainsi estimer le volume de roches dans un cône de déjection au pied d'une montagne, ou même la quantité de matière crachée par un volcan lors d'une éruption.
Le calcul du volume d'un cône permet de traduire une forme observée dans la nature en une donnée chiffrée. C’est la première étape vers des analyses plus complexes, comme l'évaluation des risques naturels.
Mais cette formule trouve aussi sa place dans des secteurs de pointe.
L'optimisation en aérospatiale et en alimentation
Le monde de l'aérospatiale s'appuie lui aussi sur la géométrie du cône. Le nez des fusées, par exemple, a souvent une forme conique. Cette conception n'est pas un hasard : elle vise à optimiser l’aérodynamisme et à réduire la friction avec l'air durant le décollage. Le calcul précis du volume intérieur est donc vital pour y placer des instruments ou d'autres composants essentiels.
Même dans notre assiette, ou presque, cette formule a son mot à dire. L'industrie agroalimentaire s'en sert constamment pour :
- Concevoir des emballages, comme les cornets de crème glacée, afin qu'ils contiennent un volume de produit bien précis.
- Optimiser la forme des silos à grains, dont la base est souvent conique pour que les céréales s'écoulent plus facilement.
- Contrôler le dosage dans les usines qui utilisent des entonnoirs ou des trémies de forme conique.
Ces quelques exemples montrent à quel point cette formule mathématique est polyvalente. Sa pertinence est d'ailleurs au cœur de nombreuses recherches en mathématiques appliquées. En France, la région PACA s'est montrée particulièrement dynamique dans ce secteur, avec une croissance marquée des publications scientifiques sur la modélisation volumétrique entre 2013 et 2020. Pour en savoir plus, vous pouvez consulter le rapport du HCERES de 2022.
Finalement, savoir comment calculer le volume d'un cône, c'est bien plus qu'une simple compétence scolaire. C'est maîtriser un outil qui connecte les mathématiques à d'innombrables facettes de notre monde. D'ailleurs, le cône est géométriquement très proche d'une autre forme très courante. Pour aller plus loin, jetez un œil à notre article qui explique comment calculer l'aire d'un cylindre.
Testez vos connaissances avec des exercices corrigés
Rien ne vaut la pratique pour vraiment maîtriser une notion mathématique. Maintenant que vous avez exploré la théorie derrière la formule du volume d'un cône, il est temps de mettre les mains à la pâte. Cette section vous guide à travers des exercices de difficulté croissante pour solidifier votre compréhension.
En partant d’un calcul simple pour aller vers des problèmes plus complexes, vous allez développer une véritable aisance. Chaque exercice est suivi d’une correction détaillée qui va au-delà de la simple réponse : elle décortique la logique de chaque étape. C'est le moment idéal pour consolider vos acquis.
Exercice 1 : Calcul direct du volume
Commençons en douceur avec un cas de figure classique. Imaginez un cône de révolution avec une base circulaire de 6 centimètres (cm) de rayon et une hauteur de 10 cm. Quel est son volume?
Correction détaillée
Pour ce premier défi, on applique directement la formule que nous connaissons bien : V = (1/3)πr²h.
-
On rassemble nos données :
- Rayon (r) = 6 cm
- Hauteur (h) = 10 cm
- On utilise π ≈ 3,14159
-
On calcule le carré du rayon :
r² = 6² = 36 cm² -
On applique la formule :
V = (1/3) × 3,14159 × 36 cm² × 10 cm
V = (1/3) × 3,14159 × 360 cm³
V ≈ 376,99 cm³
Le volume de ce cône est donc d'environ 377 cm³. C'est un excellent point de départ pour s'assurer que l'application de base est bien comprise.
Exercice 2 : Trouver une dimension manquante
Maintenant, changeons un peu la perspective. Vous avez un entonnoir conique qui peut contenir 500 millilitres (soit 500 cm³) de liquide. Son ouverture a un diamètre de 16 cm. Quelle est la hauteur de cet entonnoir?
Correction détaillée
Cette fois, on connaît le volume et le rayon, mais la hauteur nous échappe. Il faut donc manipuler un peu notre formule.
La formule V = (1/3)πr²h peut être réarrangée pour isoler la hauteur : h = (3 × V) / (πr²). Savoir manipuler une équation comme celle-ci est une compétence clé en algèbre.
-
Identifions ce qu'on sait :
- Volume (V) = 500 cm³
- Diamètre = 16 cm, ce qui signifie que le rayon (r) = 8 cm. Attention à ne pas tomber dans le piège!
-
Appliquons notre formule transformée :
h = (3 × 500 cm³) / (3,14159 × 8²)
h = 1500 cm³ / (3,14159 × 64 cm²)
h = 1500 cm³ / 201,06 cm²
h ≈ 7,46 cm
La hauteur de l'entonnoir est d'environ 7,5 cm. Si ce genre de manipulation d'équation vous donne du fil à retordre, un accompagnement personnalisé peut faire toute la différence. N'hésitez pas à explorer les options de tutorat en maths pour bâtir des bases solides.
Exercice 3 : Problème concret
Place à un scénario du monde réel! Un silo agricole, en forme de cône inversé, se remplit de grains à un débit constant de 2 mètres cubes par minute. Ce silo mesure 9 mètres de haut et son rayon à la base (en haut) est de 4 mètres. Combien de temps faudra-t-il pour le remplir complètement?
Correction détaillée
Ce problème combine notre calcul de volume avec une notion de débit. C'est un excellent exemple de l'utilité des maths au quotidien!
-
D'abord, calculons le volume total du silo :
V = (1/3)πr²h
V = (1/3) × 3,14159 × (4 m)² × 9 m
V = (1/3) × 3,14159 × 16 m² × 9 m
V ≈ 150,8 m³ -
Ensuite, calculons le temps de remplissage :
Temps = Volume total / Débit
Temps = 150,8 m³ / 2 m³/minute
Temps ≈ 75,4 minutes
Il faudra environ 75 minutes et 24 secondes pour que le silo soit plein.
Questions fréquentes sur le calcul du volume
Même après avoir exploré la formule et ses applications, il est tout à fait normal que quelques questions persistent. Le calcul du volume d'un cône amène souvent son lot d'interrogations pratiques qui méritent des réponses claires.
C'est le moment de lever les derniers doutes pour que vous puissiez aborder n'importe quel problème avec une confiance totale. Voici les questions les plus courantes, avec des explications directes et faciles à retenir.
Faut-il utiliser la hauteur ou l'apothème?
Voilà l'une des confusions les plus fréquentes, et c'est une excellente question! Pour le calcul du volume, vous devez toujours, toujours utiliser la hauteur (h). La hauteur, c'est la distance qui part bien droit du sommet du cône jusqu'au centre de sa base, formant un angle parfait de 90 degrés.
L'apothème (parfois appelée la génératrice) est différente. C'est la longueur de la « pente » du cône, mesurée du sommet jusqu'au bord de la base. Elle est essentielle pour calculer l'aire de la surface latérale, mais elle n'a pas sa place dans la formule du volume. Un truc simple à retenir : pour le volume, on pense « vertical », donc on prend la hauteur.
Cette formule fonctionne-t-elle si le cône est oblique?
Oui, absolument! C'est l'un des aspects les plus fascinants de la géométrie. Grâce à un principe mathématique puissant, le principe de Cavalieri, le volume d'un cône oblique (celui dont le sommet n'est pas pile au-dessus du centre de la base) est exactement le même que celui d'un cône droit.
Tant que l'aire de la base (πr²) et la hauteur perpendiculaire (h) restent identiques, l'inclinaison du cône ne change absolument rien à son volume. La formule V = (1/3)πr²h demeure donc parfaitement valide.
Que faire si un cône est tronqué?
Un cône tronqué, c'est simplement un cône auquel on a coupé la pointe. On se retrouve donc avec une deuxième base circulaire, plus petite, au sommet. Pour calculer son volume, la méthode la plus intuitive est celle de la soustraction. C'est comme enlever une part d'un gâteau déjà découpé.
Il suffit d'imaginer le grand cône d'origine, avant qu'il ne soit coupé.
- Calculez le volume de ce grand cône initial.
- Calculez ensuite le volume du petit cône qui a été retiré (la pointe).
- Soustrayez le volume du petit cône de celui du grand.
Le résultat obtenu est le volume exact de la partie tronquée qu'il vous reste. Maîtriser ces petites nuances demande de la pratique et de bonnes stratégies d'étude. Pour aller plus loin, découvrez nos conseils sur comment étudier efficacement afin de mieux retenir ces concepts.
Si votre enfant a besoin d'un petit coup de pouce pour transformer ces concepts en succès scolaires, Centrétudes offre un accompagnement personnalisé en mathématiques et dans bien d'autres matières. Découvrez nos services de tutorat pour l'aider à bâtir sa confiance et son autonomie.


