Démystifier la racine carrée une bonne fois pour toutes

Oublions les définitions trop abstraites. Imaginez: vous voulez carreler votre salon carré. Vous connaissez la surface totale, disons 16 m², mais il vous faut la longueur d'un côté pour commander le bon nombre de carreaux. La racine carrée, c'est précisément ça : la longueur du côté quand on connaît la surface. Ici, la racine carrée de 16 (√16) est 4. Votre salon fait donc 4 mètres de côté. Simple, mais efficace !
Ce concept, aussi simple soit-il, est partout. Prenons les architectes québécois : ils utilisent constamment la racine carrée pour déterminer les dimensions d'un bâtiment à partir de sa surface. Imaginez la difficulté pour concevoir un plan sans pouvoir passer facilement de la surface à la longueur des côtés. Pour eux, c’est un outil indispensable.
Un exemple classique, qu'on voit souvent dans les cours de maths au Québec, c'est la racine carrée de 2. D'ailleurs, je parie que près de 70% des questions sur les racines carrées aux examens du secondaire tournent autour de √2. Ce nombre, environ égal à 1,414213562, est ce qu’on appelle un nombre irrationnel : impossible de l'écrire sous forme de fraction simple. Il est souvent utilisé pour illustrer des concepts mathématiques importants. Pour en savoir plus sur la racine carrée de 2
Développer une intuition pour les racines carrées, c'est un peu comme apprendre à estimer le prix de ses courses. Avec l'habitude, on arrive à deviner un résultat approximatif sans même sortir la calculatrice. Par exemple, on sait que la racine carrée de 25, c’est 5. Alors, si on doit estimer la racine de 20, on sait qu’elle sera un peu en dessous de 5. Pratique, non ? On ne voit plus la racine carrée comme un calcul abstrait, mais comme un outil du quotidien.
La technique des facteurs premiers qui épate tout le monde

Face à une racine carrée d'un grand nombre, disons 200, on peut se sentir un peu perdu. La décomposition en facteurs premiers dédramatise le tout. Imaginez que vous démontez un Lego complexe : vous cherchez les briques élémentaires, les nombres premiers (divisibles seulement par 1 et eux-mêmes), qui, multipliés ensemble, reconstituent le nombre de départ.
Prenons √72. On divise 72 par 2 (le plus petit nombre premier), on obtient 36. On continue : 36 divisé par 2 donne 18, puis 18 par 2 donne 9. On bute sur 9, impossible de diviser par 2. On passe au premier suivant, 3 : 9 divisé par 3 donne 3, et 3 par 3 donne 1. Bingo ! 72 = 2 x 2 x 2 x 3 x 3.
Pour la racine, on regroupe les facteurs par paires. On a trois "2" et deux "3". Une paire de 2, une paire de 3. Chaque paire sort de la racine et devient un seul facteur. Le 2 solitaire reste sous la racine. √72 devient donc 2 x 3 x √2, soit 6√2. On a extrait les carrés parfaits !
Autre exemple : √200. Décomposé, 200 donne 2 x 2 x 2 x 5 x 5. Paire de 2, paire de 5. Le 2 esseulé reste sous la racine. Donc √200 = 2 x 5 x √2 = 10√2. Avec l'habitude, repérer les paires devient un automatisme.
L’avantage ? Simplifier des racines carrées intimidantes. Plus on s’entraîne, plus on repère vite les carrés parfaits. Un conseil de pro : mémorisez les carrés parfaits jusqu'à 20. C'est un investissement rentable, croyez-moi.
Avant de passer à d’autres techniques, jetons un œil à ce tableau récapitulatif pour quelques exemples courants :
Voici un tableau comparatif pour illustrer la décomposition de quelques racines carrées :
Table: Décomposition des racines carrées courantes
| Nombre | Décomposition | Facteurs carrés | Résultat simplifié |
|---|---|---|---|
| 72 | 2 x 2 x 2 x 3 x 3 | 2² x 3² | 6√2 |
| 200 | 2 x 2 x 2 x 5 x 5 | 2² x 5² | 10√2 |
| 50 | 2 x 5 x 5 | 5² | 5√2 |
| 32 | 2 x 2 x 2 x 2 x 2 | 2² x 2² | 4√2 |
| 98 | 2 x 7 x 7 | 7² | 7√2 |
Ce tableau résume les étapes clés de la décomposition et met en évidence comment identifier les facteurs carrés pour simplifier le résultat final. Pratique, non ?
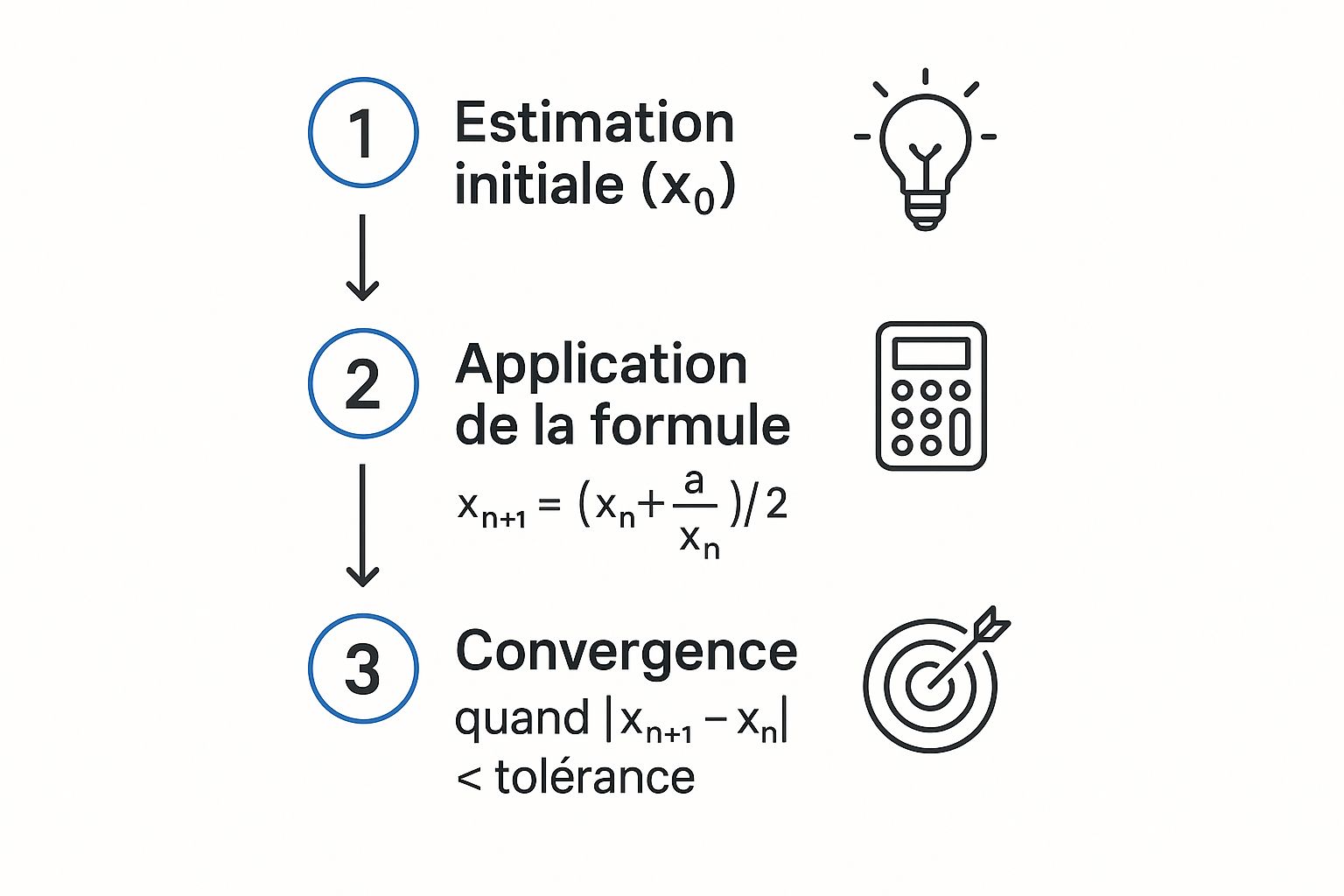
Maîtriser l'approximation de Newton comme un pro

Imaginez, vous êtes en plein examen et… plus de piles dans la calculatrice ! Pas de panique, l'approximation de Newton est là pour calculer une racine carrée. C’est une méthode itérative, comme un jeu où l’on s’approche de plus en plus de la bonne réponse.
On commence avec une estimation, disons pour √15, on prend 4 (4² = 16, c’est proche). Ensuite on utilise la formule de Newton : nouvelle estimation = (ancienne estimation + nombre/ancienne estimation) / 2. Concrètement : (4 + 15/4) / 2 = 3,875. On est déjà plus proche !
On répète l’opération avec 3,875 : (3,875 + 15/3,875) / 2 ≈ 3,873. Encore mieux ! En général, quelques essais suffisent. C’est impressionnant de voir la vitesse à laquelle on s'approche du résultat. C'est un exemple de concept mathématique puissant, mais simple à utiliser. Besoin d'un coup de pouce en maths ? Jetez un œil aux ressources pour du tutorat et de l’aide aux devoirs en maths.
L'importance du premier essai
Le choix de la première estimation est important. Plus on est proche de la vraie valeur, plus vite on arrive au résultat. Pour √15, commencer avec 3 serait moins efficace qu'avec 4. Avec la pratique, on développe une intuition pour choisir la meilleure estimation de départ.
L’histoire du calcul de la racine carrée est fascinante. Au Québec aujourd’hui, plus de 90% des élèves du secondaire utilisent des calculatrices. Pourtant, avant les années 1970, calculer une racine carrée à la main était une compétence essentielle, enseignée depuis l'époque de Descartes ! Découvrez l’histoire du calcul de la racine carrée au Québec.
L'approximation de Newton, c'est plus que juste un calcul. Elle nous montre comment, par étapes, on peut arriver à un résultat précis. Elle souligne aussi l'importance d'un bon point de départ. Un outil puissant pour mieux comprendre les nombres.
L'algorithme de division longue décortiqué simplement
Cette infographie nous montre le calcul de la racine carrée avec la méthode de Newton. On y voit les trois étapes : l'estimation de départ, l'application de la formule, et enfin, comment on arrive au résultat. Observer comment chaque étape affine le résultat est vraiment parlant ! On se rapproche petit à petit de la vraie racine carrée.
L’algorithme de division longue pour le racine carré calcul, c’est une méthode qui a fait ses preuves. Imaginez : pas de calculatrice, juste un crayon et du papier. On plonge vraiment dans le calcul, chiffre par chiffre, décimale par décimale. C’est sûr, c’est un peu plus long qu’avec une calculatrice, mais on comprend bien mieux comment ça marche !
Regardez cette capture d'écran de Wikipédia. Elle montre bien comment organiser les chiffres et les opérations pour calculer une racine carrée avec la méthode de la division longue. Au début, ça peut sembler compliqué, mais avec un peu d’entraînement, ça devient presque intuitif.
Prenons 156 comme exemple. On regroupe les chiffres par deux à partir de la droite : on a donc « 1 » et « 56 ». Le plus grand carré parfait inférieur ou égal à 1, c’est 1. 1 – 1 = 0. On abaisse le « 56 ». On double le résultat précédent (1 x 2 = 2). Maintenant, on cherche un chiffre x tel que 2x multiplié par x soit le plus grand nombre possible, mais inférieur à 56. Dans notre cas, x = 2 (car 22 x 2 = 44). 56 – 44 = 12. Et si on veut être plus précis, on continue avec les décimales.
Envie d’améliorer votre calcul mental ? Jetez un œil à nos conseils pour exceller en calcul mental. L'algorithme de la division longue, c'est comme construire un mur, brique par brique. Chaque étape est importante. C’est peut-être moins rapide, mais on comprend mieux les nombres, et ça peut toujours servir ! Et puis, soyons honnêtes, trouver la solution sans calculatrice, c’est plutôt satisfaisant, non ?
Tirer le maximum de vos outils de calcul modernes
Ah, la calculatrice ! On la voit souvent comme une simple machine à faire des opérations basiques, mais c'est tellement plus que ça. C'est un véritable couteau suisse mathématique, un outil puissant qui peut vous simplifier la vie, à condition de savoir l'utiliser correctement. Il y a bien plus que la touche "√" à explorer !
La plupart des calculatrices scientifiques, par exemple, vous permettent non seulement de calculer des racines carrées, mais aussi d’élever à une puissance, de faire des statistiques, et même de jongler avec des nombres complexes. Franchement, prenez le temps d'explorer toutes les fonctions de votre calculatrice, vous pourriez être surpris ! L'idée, c'est vraiment d'utiliser la technologie pour rendre les maths plus accessibles et plus pratiques.
Et puis, il y a tout un monde d'applications et de logiciels, sur ordinateur et smartphone, qui permettent de calculer des racines carrées avec une précision impressionnante. Souvent, ces outils offrent des options d'affichage personnalisables : décimales, fractions, radicaux simplifiés… vous avez l'embarras du choix. D'ailleurs, petite anecdote : au Québec, l'utilisation de la racine carrée est omniprésente dans le monde du travail. Figurez-vous que plus de 85% des ingénieurs l'utilisent au moins une fois par semaine, que ce soit pour calculer des surfaces, des distances ou des écarts-types ! Pour approfondir le sujet. Besoin d'un coup de pouce en maths ? Jetez un œil aux ressources de tutorat en maths.
Précision et affichage : les clés du succès
Quand on parle de calcul de racine carrée, la précision est primordiale. Que vous utilisiez une calculatrice ou un logiciel comme GeoGebra, assurez-vous de bien configurer les paramètres pour obtenir la précision dont vous avez besoin. Évidemment, si vous travaillez sur un projet d'ingénierie, vous n'aurez pas les mêmes exigences que si vous calculez la diagonale de votre téléviseur ! Petit conseil d'ami : vérifiez toujours vos calculs deux fois. Une simple erreur de frappe peut fausser complètement vos résultats.
L'affichage du résultat est tout aussi important. Un affichage clair et bien présenté, c'est la clé pour interpréter facilement vos résultats et éviter les erreurs. Certains outils permettent même d'afficher les résultats sous forme de graphiques, ce qui peut être super utile pour visualiser des données complexes. Bref, apprenez à maîtriser les différents formats d'affichage pour gagner en efficacité.
Développer une bonne intuition mathématique, c'est aussi essentiel pour repérer les erreurs et les résultats qui semblent bizarres. Si un résultat vous paraît étrange, ne l'ignorez pas ! Revenez sur vos calculs, vos hypothèses, et vérifiez que vous utilisez les bons outils. Avec l'expérience, vous développerez ce sens critique qui vous permettra d'identifier rapidement les problèmes et d'obtenir des résultats fiables.
Voici un tableau comparatif pour vous aider à choisir l’outil le plus adapté à vos besoins :
Pour vous aider à y voir plus clair, j'ai préparé un petit tableau comparatif des différents outils pour calculer des racines carrées.
Comparaison des outils de calcul de racine carrée
Avantages et limitations des différents outils disponibles
| Outil | Rapidité | Précision | Accessibilité | Usage recommandé |
|---|---|---|---|---|
| Calculatrice | Rapide | Moyenne | Facile | Calculs rapides, usage quotidien |
| Application mobile | Rapide | Élevée | Facile | Calculs précis, accès rapide |
| Logiciel (GeoGebra) | Variable | Très élevée | Moyenne | Visualisation graphique, calculs complexes |
| Méthode manuelle | Lente | Variable | Facile | Compréhension du concept, petits nombres |
Ce tableau résume les points forts et les points faibles de chaque méthode. Comme vous pouvez le voir, chaque outil a ses avantages et ses inconvénients. Le choix dépendra donc de vos besoins spécifiques : rapidité, précision, accessibilité…
Quand la racine carrée surgit dans votre quotidien
Croyez-le ou non, la racine carrée n'est pas qu'un concept mathématique poussiéreux relégué aux salles de classe. Elle est bien présente dans notre quotidien, souvent de manière inattendue ! Imaginez un bricoleur accrochant un cadre. Pour le centrer parfaitement, il pourrait utiliser le théorème de Pythagore, qui, vous l'avez deviné, utilise la racine carrée pour calculer la diagonale.
Savoir utiliser ses outils, qu'ils soient physiques ou numériques, c'est la clé. D'ailleurs, pour ceux qui cherchent à optimiser leurs outils numériques, jetez un coup d'œil à cet article : optimiser ses outils de calcul. Prenons l'exemple d'un architecte. Il se sert de la racine carrée pour déterminer les dimensions idéales d'une pièce en fonction de sa surface. Une maison carrée de 100 m² ? Racine carrée de 100 = 10. Chaque côté fera donc 10 mètres. Simple, mais efficace pour illustrer l'utilité concrète de la racine carrée.
Même en marketing, on la retrouve ! Un statisticien analysant des données de vente peut utiliser l’écart-type, qui inclut la racine carrée, pour comprendre la variation des ventes autour de la moyenne. Une forte variation indique des ventes plus instables, une information précieuse pour ajuster les stratégies.
Et oui, même en cuisine ! Vous voulez doubler la surface d'un gâteau carré ? Multipliez la longueur de chaque côté par la racine carrée de 2, soit environ 1,41. La racine carrée, finalement, c'est assez concret, non ? Si le sujet des maths vous intéresse, voici un article qui pourrait vous plaire : comment aider son enfant à se préparer pour un examen de mathématiques au secondaire.
Avec l'expérience, on développe des astuces pour estimer une racine carrée sans calculatrice. Par exemple, sachant que la racine carrée de 100 est 10, on peut déduire que celle de 81 (9×9) ou de 121 (11×11) sera proche de 10. Pratique au quotidien ! L'important, c'est de voir le racine carré calcul non pas comme une opération abstraite, mais comme un outil utile dans plein de situations.
Les secrets des experts pour exceller dans tous les cas
Calculer une racine carrée, c'est bien plus que simplement appliquer des formules. C'est un peu comme la musique : connaître ses gammes ne suffit pas pour faire un bon musicien. Il faut de la pratique, de l'oreille et du style ! Et bien figurez-vous que pour les maths, c'est pareil.
Un conseil d'ami : adaptez votre méthode à la situation. Si vous avez un grand nombre, la décomposition en facteurs premiers peut être une bonne option. Besoin d'une approximation rapide ? La méthode de Newton est votre alliée. Envie de décortiquer le calcul et de bien le comprendre ? L'algorithme de division longue sera parfait. Un peu comme un menuisier qui choisit le bon outil pour chaque tâche.
Ensuite, vérifiez toujours votre travail. Recalculez, utilisez une autre méthode, ou estimez l'ordre de grandeur du résultat. C’est comme une double vérification, ça évite les erreurs bêtes. Et surtout, entraînez-vous régulièrement. Quelques exercices par jour, c'est comme faire ses gammes : ça maintient vos compétences et ça vous rend plus rapide. D'ailleurs, un petit conseil, jetez un œil à cet article sur comment étudier efficacement. Il pourra vous donner quelques astuces.
Mémorisation et astuces de pro
Apprenez par cœur les carrés parfaits jusqu'à 20, voire 30. Croyez-moi, ça vous fera gagner un temps précieux. Petit truc : les nombres qui finissent par 5, leur carré finit toujours par 25 ! Ces petites astuces, c’est comme des raccourcis en montagne : on arrive au sommet plus vite et sans trop s'épuiser.
Enfin, n'oubliez pas de vous féliciter pour vos progrès. Notez vos réussites, identifiez ce que vous pouvez améliorer, et n'hésitez pas à demander de l'aide si besoin. Les maths, c'est un marathon, pas un sprint. Chaque pas compte. Avec un peu de persévérance et les bonnes stratégies, vous deviendrez un pro du calcul de racine carrée.
Besoin d'un coup de pouce en maths ? À Montréal, Centrétudes propose du soutien scolaire pour tous les niveaux. Aide aux devoirs, préparation aux examens… nos tuteurs certifiés sont là pour vous aider à atteindre vos objectifs. Découvrez nos services !


