Bien plus qu'un simple exercice scolaire, l'addition de fractions est une compétence pratique que l'on utilise bien plus souvent qu'on ne le pense. La maîtriser, c'est se donner les outils pour résoudre une foule de problèmes concrets, que ce soit pour ajuster une recette de cuisine, mesurer des matériaux de construction ou même mieux comprendre des statistiques.
Pourquoi l'addition de fractions est une compétence essentielle
Loin d'être une notion abstraite réservée aux salles de classe, la capacité d'additionner des fractions se manifeste constamment dans nos vies. Imaginez que vous préparez un gâteau. La recette demande 1/2 tasse de farine, mais vous décidez d'ajouter un autre ingrédient qui en contient déjà 1/4 de tasse. Savoir comment combiner ces quantités avec précision est une application directe et utile de l'addition de fractions.

Au-delà de ces exemples du quotidien, cette compétence vient renforcer des aptitudes beaucoup plus profondes.
- Ça développe la pensée logique. En cherchant un dénominateur commun, on apprend à trouver un terrain d'entente entre différents éléments, une compétence clé dans la résolution de problèmes en général.
- C'est la fondation des maths avancées. La maîtrise des fractions est un prérequis indispensable pour bien naviguer dans l'algèbre, les pourcentages et les probabilités plus tard.
- Ça renforce la confiance en soi. Réussir à surmonter une notion souvent perçue comme difficile donne aux élèves la confiance nécessaire pour s'attaquer à des défis encore plus complexes.
D'ailleurs, une enquête menée auprès de 1 200 enseignants en mathématiques au Canada francophone le confirme : 95 % d'entre eux reconnaissent que la compréhension des fractions est un socle indispensable pour réussir en algèbre et en statistiques. Ces disciplines sont au cœur du parcours au secondaire et dans l'enseignement supérieur.
L'addition de fractions, ce n'est pas seulement un calcul. C'est un exercice de logique qui nous apprend à décomposer un problème, à trouver des équivalences et à construire une solution claire.
Cette habileté est un excellent indicateur de la capacité d'un élève à raisonner de manière structurée. Si vous cherchez des stratégies pour accompagner votre jeune, notre guide sur comment aider son enfant à réussir ses devoirs de mathématiques offre une foule de conseils pratiques pour transformer ces défis en réussites.
Trouver le dénominateur commun pour tout simplifier
Pour qu'une addition de fractions tienne la route, il faut que les deux fractions parlent la même langue. Essayer d’ajouter des tiers et des quarts, c'est un peu comme comparer des pommes et des oranges. Le dénominateur commun, c’est ce qui va nous permettre de transformer ces « parts » de gâteau différentes en morceaux de taille identique, qu’on pourra enfin combiner sans se casser la tête.

C'est ici que le fameux Plus Petit Commun Multiple (PPCM) entre en jeu. Son nom peut faire un peu peur, mais il s'agit tout simplement du plus petit nombre qui est un multiple de vos deux dénominateurs. Mettre la main dessus, c’est la clé pour garder les calculs les plus simples possible.
Dénicher le PPCM sans effort
Prenons un exemple classique : les fractions 1/3 et 1/4. On cherche donc le PPCM de 3 et 4.
- Multiples de 3 : 3, 6, 9, 12, 15…
- Multiples de 4 : 4, 8, 12, 16, 20…
Le premier nombre qui apparaît dans les deux listes est 12. Et voilà, on a trouvé notre dénominateur commun ! Pas besoin de toujours lister les multiples; une astuce rapide est de multiplier les dénominateurs entre eux : 3 x 4 = 12. Cette méthode fonctionne à tous les coups, même si elle ne donne pas toujours le plus petit multiple.
Maintenant que le dénominateur commun est trouvé, il faut ajuster chaque fraction pour qu’elle devienne équivalente. Pour 1/3, on se demande : « Par quoi multiplier 3 pour obtenir 12 ? ». La réponse est 4. On multiplie donc le haut et le bas par 4, ce qui nous donne 4/12.
On applique le même raisonnement pour 1/4. Pour passer de 4 à 12, il faut multiplier par 3. La fraction devient alors 3/12. Ça y est, nos deux fractions sont prêtes à être additionnées !
Trouver le dénominateur commun n'est pas qu'une étape de calcul. C'est avant tout un exercice de logique qui consiste à trouver un terrain d'entente entre deux nombres différents pour pouvoir les faire travailler ensemble.
Le tableau suivant résume bien ce processus de transformation.
Transformer des fractions avec un dénominateur commun
Ce tableau illustre comment convertir des fractions pour qu'elles partagent le même dénominateur, une étape essentielle avant l'addition.
| Fractions de départ | Dénominateur commun trouvé (PPCM) | Fractions équivalentes |
|---|---|---|
| 1/3 et 1/4 | 12 | 4/12 et 3/12 |
| 1/2 et 3/8 | 8 | 4/8 et 3/8 |
| 2/5 et 1/6 | 30 | 12/30 et 5/30 |
Comme on peut le voir, une fois qu'on a le PPCM, le reste n'est qu'une simple multiplication pour obtenir les nouvelles fractions prêtes à l'emploi.
Quelques astuces pratiques
Certains cas sont plus simples qu'on ne le pense. Si un dénominateur est un multiple de l’autre, comme dans 1/2 + 3/8, le plus grand des deux (ici, 8) est directement votre PPCM. Inutile de chercher plus loin !
Pour les cas un peu plus complexes, une bonne maîtrise des tables de multiplication est un atout indéniable. Et si vous voulez gagner un temps précieux, rafraîchir vos connaissances sur les critères de divisibilité peut vraiment vous aider à repérer rapidement les facteurs communs entre les dénominateurs.
L'addition de fractions, étape par étape
Une fois que vos fractions ont le même dénominateur, le plus gros du travail est derrière vous. L'addition de fraction devient alors bien plus simple et logique. Il suffit de vous concentrer sur les numérateurs, les chiffres du haut, car les dénominateurs, eux, ne bougeront plus.
C'est un peu comme si vous ajoutiez 1/4 d'heure et 2/4 d'heure. Le résultat est tout simplement 3/4 d'heure. Les « quarts » représentent vos unités de mesure, et vous avez juste additionné les quantités. Le principe est exactement le même, peu importe les fractions.
On additionne les numérateurs
La seule chose à faire à ce stade, c'est d'additionner les numérateurs entre eux. Si on reprend notre exemple des fractions équivalentes 4/12 et 3/12, le calcul est tout simple :
4 + 3 = 7
Le résultat de cette petite addition devient le numérateur de votre fraction finale. C'est tout! Vous avez maintenant toutes les pièces du casse-tête pour assembler votre réponse.
Le dénominateur, on n'y touche pas!
Le dénominateur commun que vous avez trouvé (ici, 12) reste exactement le même. Il ne faut surtout pas additionner les dénominateurs ensemble; c'est d'ailleurs l'erreur la plus courante! Votre réponse finale combine simplement le nouveau numérateur et le dénominateur commun :
4/12 + 3/12 = 7/12
Cette règle n'est pas nouvelle. En fait, des manuels scolaires québécois insistaient déjà, dès 1880, sur l'importance de mettre les fractions au même dénominateur avant de les additionner. Pour les curieux, l'histoire des fractions) montre bien comment ces méthodes se sont établies au fil du temps.
Ce visuel résume parfaitement les trois actions clés pour réussir une addition de fraction.
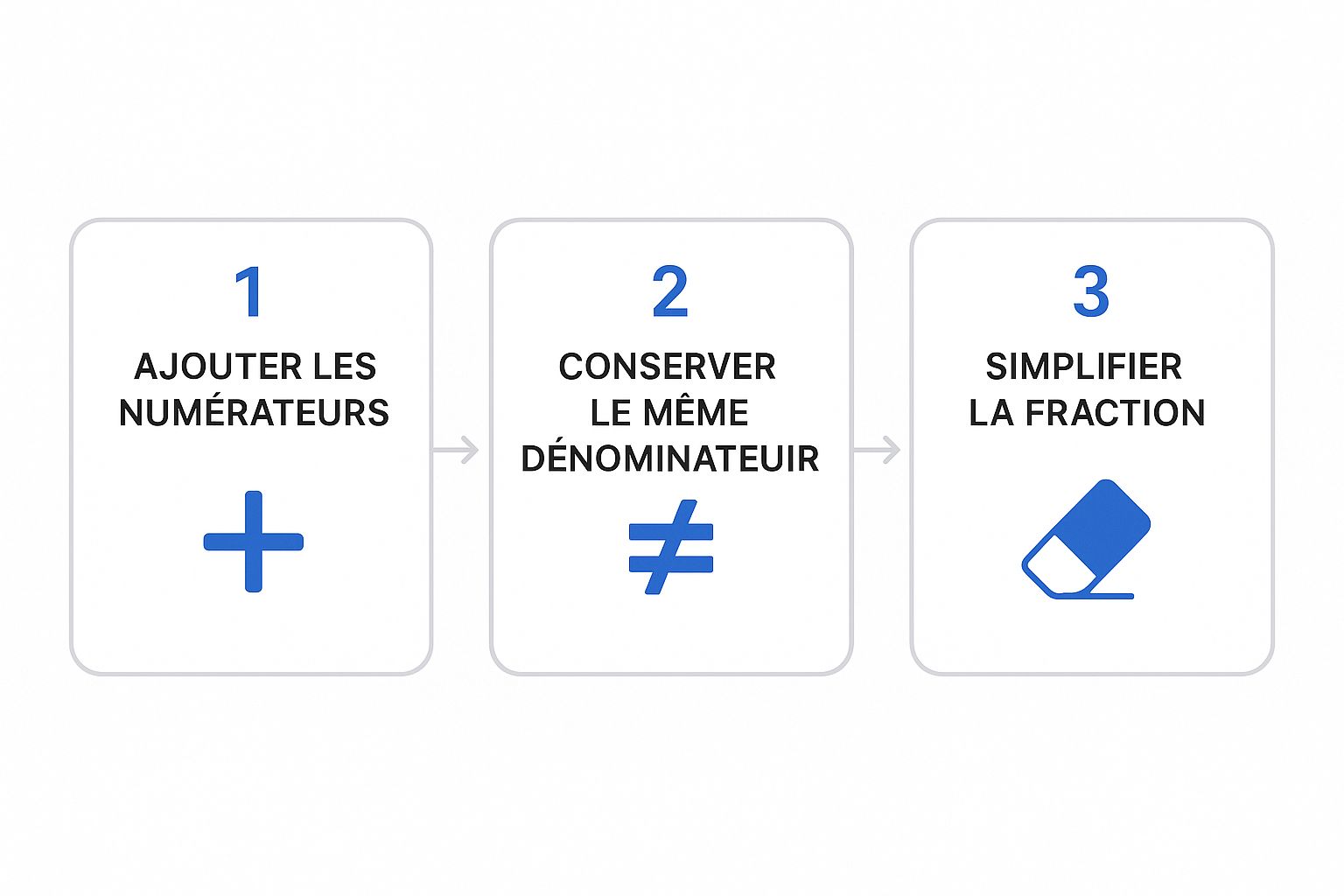
L'image montre bien que le calcul se fait sur les numérateurs, que le dénominateur est conservé, et qu'il faut toujours penser à vérifier si on peut simplifier à la fin.
Le point à retenir : Le dénominateur, c'est la taille des parts (des douzièmes, des quarts, etc.). Quand vous additionnez, vous ne changez pas la grosseur des parts, vous augmentez simplement leur nombre.
Une fois l'addition terminée, il reste une dernière petite étape pour que votre réponse soit impeccable : la simplification.
Simplifier le résultat pour une réponse parfaite
Vous avez trouvé un dénominateur commun et additionné les numérateurs. Bravo, le plus gros du travail est fait! Mais pour que votre réponse soit vraiment impeccable, il reste une touche finale : la simplification. Présenter une fraction sous sa forme la plus simple, qu’on appelle aussi irréductible, est une convention qui facilite énormément la lecture et la comparaison des résultats.

Une fraction comme 6/8 est techniquement correcte, mais avouez que 3/4 est bien plus élégant et facile à interpréter. C’est la différence entre dire « il me reste six huitièmes de la tarte » et « il me reste trois quarts de la tarte ». La deuxième version est tout de suite plus claire.
Comment réduire une fraction à sa plus simple expression
L’objectif est simple : trouver le plus grand nombre qui peut diviser à la fois le numérateur et le dénominateur. Ce nombre un peu magique, c’est le Plus Grand Commun Diviseur (PGCD).
Reprenons notre exemple, 6/8. Pour dénicher le PGCD de 6 et 8, on peut lister leurs diviseurs :
- Diviseurs de 6 : 1, 2, 3, 6
- Diviseurs de 8 : 1, 2, 4, 8
Le plus grand nombre qui apparaît dans les deux listes est 2. Voilà notre PGCD! Il ne reste plus qu’à diviser le haut et le bas de la fraction par ce nombre :
- 6 ÷ 2 = 3
- 8 ÷ 2 = 4
Et voilà, 6/8 se transforme en 3/4. Votre fraction est irréductible lorsque vous ne pouvez plus trouver de diviseur commun (autre que 1).
La simplification n'est pas qu'une question d'esthétique mathématique. C'est une étape qui prouve que vous comprenez la relation entre les nombres qui composent la fraction.
Une petite astuce rapide : si votre numérateur et votre dénominateur sont tous les deux des nombres pairs, vous pouvez être certain qu’ils sont divisibles par 2. Divisez-les, puis voyez si vous pouvez recommencer.
Pour aller plus loin et maîtriser l'art de la simplification, il est très utile de savoir ce qu'est un nombre premier. Ce sont les blocs de construction de tous les autres nombres, et ils jouent un rôle clé dans cette étape finale.
Les erreurs fréquentes à éviter absolument
Additionner des fractions peut sembler simple, mais quelques pièges classiques guettent même les plus attentifs. Connaître ces erreurs est la meilleure façon de les contourner et de gagner en confiance.
La faute la plus répandue? Additionner les dénominateurs entre eux. C'est une erreur que l'on voit tout le temps. Imaginez que vous ajoutez 1/8 de pizza et 3/8 de pizza. Vous n'obtenez pas 4/16; vous avez simplement 4 parts de la même pizza, soit 4/8. Le dénominateur définit la taille des parts, il ne change pas pendant l'addition.
L'erreur d'additionner les dénominateurs est souvent conceptuelle. Penser en termes concrets, comme des parts de gâteau ou de pizza, ancre la logique et empêche de voir les nombres comme des entités séparées.
Autres points de vigilance
D'autres erreurs peuvent facilement se glisser dans vos calculs. Il est essentiel de les identifier pour développer de bons réflexes et ne plus tomber dans le panneau.
- Mauvais calcul du dénominateur commun : Se tromper en trouvant le PPCM (Plus Petit Commun Multiple) fausse tout le reste du calcul. Prenez vraiment le temps de vérifier vos multiples; ça en vaut la peine.
- Oublier d'ajuster les numérateurs : Quand vous changez le dénominateur, le numérateur doit aussi être multiplié par le même facteur. C'est la seule façon pour que la fraction reste équivalente.
- Simplification incorrecte ou incomplète : Une fois le résultat obtenu, comme 4/8, il faut toujours le réduire à sa forme la plus simple. Dans ce cas-ci, c'est 1/2. C'est une étape souvent oubliée sous la pression d'un examen!
Des études montrent que l'utilisation de supports visuels améliore la mémorisation de la règle pour 92 % des élèves, ce qui aide grandement à éviter ces pièges.
La pratique régulière reste le facteur clé du succès. Pour vous aider, nos conseils pour exceller en calcul mental peuvent vous aider à renforcer ces automatismes et à devenir plus rapide et plus sûr de vous.
Additionner des fractions : démystifier les questions fréquentes
Même quand on pense maîtriser les étapes, certaines situations peuvent encore nous faire hésiter. C'est tout à fait normal. Regardons ensemble les questions qui reviennent le plus souvent pour vraiment solidifier vos connaissances sur l'addition de fraction et vous donner confiance.
Que faire avec un nombre entier?
Une question classique : comment additionner une fraction avec un nombre entier? C'est beaucoup plus simple que ça en a l'air. Il suffit de voir le nombre entier comme une fraction. Pour ça, on lui donne simplement un dénominateur de 1.
Par exemple, le chiffre 3 devient 3/1. Facile, non?
Une fois cette transformation faite, on applique la méthode habituelle. Disons qu'on veut calculer 3 + 1/4.
- On transforme d'abord 3 en 3/1.
- Ensuite, on cherche le dénominateur commun, qui est évidemment 4.
- On ajuste la première fraction pour qu'elle ait ce dénominateur : le calcul devient 12/4 + 1/4, ce qui nous donne 13/4.
La règle d'or : ne jamais additionner les dénominateurs
C'est LA règle à ne jamais oublier, mais pourquoi est-elle si cruciale? Pensez à une pizza coupée en 8 pointes (notre dénominateur). Si vous prenez 1 pointe (1/8), puis 2 autres pointes (2/8), vous avez mangé 3 pointes au total.
Ce qui est important de comprendre, c'est que la taille de chaque pointe n'a pas changé. La pizza est toujours coupée en huitièmes. Vous avez donc mangé 3/8 de la pizza. Le dénominateur, c'est l'unité de mesure – la « grosseur de la pointe » – et elle doit rester la même tout au long de l'addition.
L'astuce la plus simple pour trouver un dénominateur commun? Multipliez les deux dénominateurs. Pour 1/4 + 2/5, le dénominateur commun sera 4 x 5 = 20. C'est une méthode qui fonctionne à tous les coups, même si ça demande parfois de simplifier un peu plus le résultat final.
Comprendre ces détails fait toute la différence. Si les fractions restent un casse-tête, un accompagnement personnalisé peut vraiment aider à débloquer la situation. Le tutorat en maths est une excellente ressource pour renforcer ces compétences et bâtir des bases solides pour l'avenir.
Chez Centretudes, nous transformons les défis mathématiques en réussites. Découvrez comment nos tuteurs peuvent aider votre enfant à exceller en visitant https://centretudes.ca.


