Quand on parle de multiplier des fractions, la règle est étonnamment directe : on multiplie les numérateurs entre eux, puis on multiplie les dénominateurs entre eux. Voilà, c'est tout! Cette simplicité transforme souvent un sujet qui semble intimidant en l'une des opérations les plus faciles en mathématiques.
Pourquoi multiplier des fractions est plus simple qu'il n'y paraît

Mettez de côté les souvenirs parfois compliqués des cours de maths. Contrairement à l'addition ou à la soustraction, la multiplication des fractions n'exige pas de se casser la tête à trouver un dénominateur commun. Le processus est beaucoup plus direct.
Le secret, c'est de bien saisir ce que « multiplier » veut dire ici. Concrètement, ça revient souvent à prendre une fraction d'une fraction. Imaginez que vous avez la moitié (1/2) d'une tarte et que vous voulez en donner un tiers (1/3) à un ami. Vous prenez donc 1/3 de 1/2. Ce petit mot « de », c’est la clé; en maths, il se traduit très souvent par une multiplication.
Visualiser le concept pour mieux comprendre
Penser en images, ça aide énormément. Si vous prenez la moitié d'une pizza, puis que vous coupez cette moitié en trois parts égales, chaque morceau représente en fait un sixième (1/6) de la pizza de départ. Le calcul le confirme sans détour : 1/2 x 1/3 = 1/6.
Cette logique visuelle explique pourquoi la règle fonctionne si bien :
- Les numérateurs (les chiffres du haut) vous disent combien de parts vous prenez.
- Les dénominateurs (les chiffres du bas) définissent en combien de parts le tout a été divisé.
En multipliant les numérateurs, vous calculez le nombre de parts que vous aurez à la fin. En multipliant les dénominateurs, vous déterminez la nouvelle taille de chaque part par rapport à l'ensemble.
L'idée n'est pas seulement de mémoriser une formule, mais de bâtir une intuition. Quand vous multipliez deux fractions plus petites que 1, attendez-vous toujours à un résultat encore plus petit. C'est logique : vous prenez une portion d'une portion qui était déjà plus petite que l'entier.
Cette compétence est un pilier du parcours scolaire. La maîtrise de la multiplication des fractions est essentielle pour résoudre des problèmes concrets, comme calculer les deux tiers d'une somme d'argent. C’est un outil indispensable pour attaquer des notions plus complexes.
Une base solide vous permettra non seulement de savoir comment multiplier des fractions, mais aussi de comprendre pourquoi la méthode est la bonne. Cette confiance est un atout majeur pour développer de solides aptitudes en maths et gagner en rapidité. Pour aller plus loin, jetez un œil à nos conseils pour exceller en calcul mental.
La méthode de multiplication expliquée pas à pas
Maintenant que la théorie est claire, passons à la pratique. La beauté de la multiplication de fractions, c’est sa simplicité. Le processus se résume à deux actions fondamentales, sans détours ni complications.
L'objectif est que cette méthode devienne un réflexe. Pour y arriver, commençons par un calcul très simple avant d’explorer des cas un peu plus complexes. Cette approche progressive vous aidera à bâtir votre confiance étape par étape.
Le cœur de la méthode pour multiplier les fractions
La règle d'or est étonnamment directe :
- Multiplier les numérateurs entre eux pour trouver le nouveau numérateur.
- Multiplier les dénominateurs entre eux pour obtenir le nouveau dénominateur.
Prenons un exemple concret pour bien visualiser : la multiplication de 1/2 par 3/4.
D'abord, on s'occupe des numérateurs, les chiffres du haut : 1 x 3 = 3. Voilà, le numérateur de notre réponse est 3.
Ensuite, on fait la même chose avec les dénominateurs, les chiffres du bas : 2 x 4 = 8. Le dénominateur final sera donc 8.
Le résultat de 1/2 x 3/4 est tout simplement 3/8. Pas besoin de trouver un dénominateur commun, ce qui rend cette opération bien plus rapide que l’addition ou la soustraction. Bien sûr, une bonne connaissance de ses tables est un atout majeur ici. Si vous avez besoin d'une petite révision, notre guide sur les tables de multiplication peut vraiment vous aider.
Le diagramme ci-dessous résume visuellement ce processus simple en trois temps.
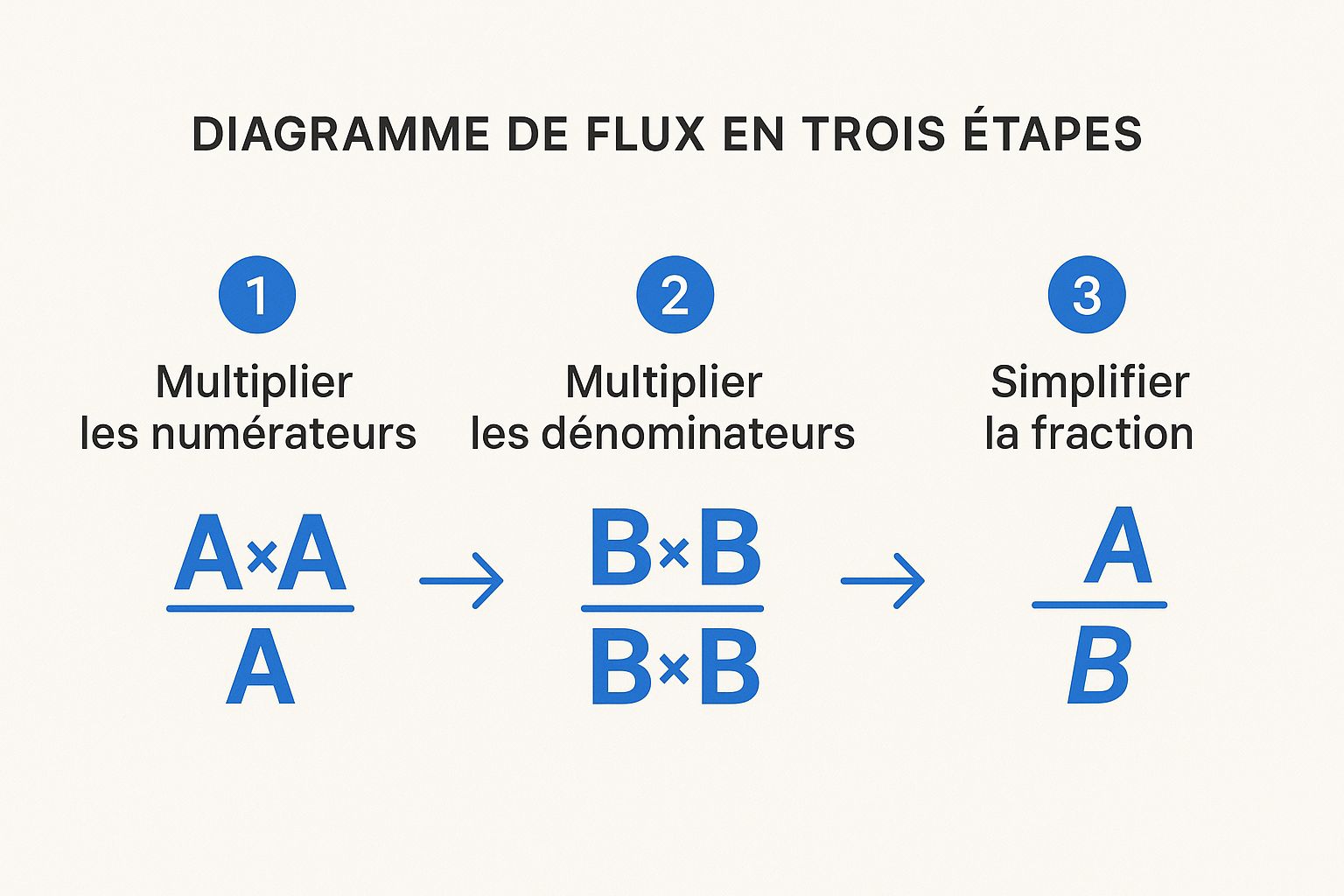
Cette image le confirme : le chemin est direct. On multiplie en haut, on multiplie en bas, et on simplifie si nécessaire.
Un autre exemple pour consolider la méthode
Augmentons un peu la difficulté. Imaginons que nous devions calculer 2/5 x 3/7. En suivant la même logique, on procède en deux temps.
Premièrement, le calcul des numérateurs :
- On prend les chiffres du haut, soit 2 et 3.
- On les multiplie ensemble : 2 x 3 = 6.
Deuxièmement, on fait de même pour les dénominateurs :
- On identifie les chiffres du bas, c'est-à-dire 5 et 7.
- On effectue la multiplication : 5 x 7 = 35.
Le résultat de notre opération est donc 6/35. La dernière étape, et non la moindre, est de toujours vérifier si la fraction peut être simplifiée. Dans ce cas-ci, 6 et 35 n'ont aucun diviseur commun à part 1. La fraction 6/35 est donc déjà sous sa forme la plus simple, qu'on appelle aussi irréductible.
La clé, c'est la rigueur. Même si le calcul semble facile, prenez toujours le temps de bien identifier les numérateurs et les dénominateurs. Cette discipline évite les erreurs d'inattention, surtout lorsque les chiffres deviennent plus grands ou que plusieurs fractions sont impliquées dans le même calcul. Une bonne organisation, c'est la moitié du travail de fait
L'art de simplifier pour des calculs plus rapides
Obtenir la bonne réponse, c’est bien. Mais la présenter dans sa forme la plus simple, ce qu’on appelle une fraction irréductible, c’est encore mieux. C’est le détail qui transforme un bon résultat en un résultat impeccable. Pour y arriver, il existe une technique astucieuse qui peut vraiment alléger vos calculs.
On peut s'attaquer à la simplification à deux moments clés. La méthode classique consiste à multiplier d'abord, puis à réduire la fraction finale. C'est une approche fiable, mais qui peut rapidement vous laisser avec de grands nombres, rendant la simplification plus ardue.
La simplification croisée: une technique puissante
Heureusement, il y a une approche plus stratégique : simplifier avant même de multiplier. Cette technique, connue sous le nom de simplification croisée, est un véritable raccourci. Le principe est de diviser un numérateur et un dénominateur par un diviseur commun, même s'ils ne sont pas dans la même fraction.
En manipulant des nombres plus petits dès le départ, le risque d'erreur de calcul diminue considérablement. C'est une méthode qui rend tout le processus plus fluide et souvent beaucoup plus rapide.
Prenons un exemple concret : vous devez multiplier 4/9 x 3/8.
Sans simplification croisée, vous feriez :
- 4 x 3 = 12
- 9 x 8 = 72
- Le résultat est 12/72, qu’il faut ensuite réduire.
Maintenant, avec la simplification croisée, vous remarquez que :
- Le 4 au numérateur et le 8 au dénominateur sont tous les deux divisibles par 4.
- Le 3 au numérateur et le 9 au dénominateur sont tous les deux divisibles par 3.
Votre calcul se transforme alors en 1/3 x 1/2, ce qui donne directement 1/6. C'est exactement le même résultat, mais obtenu avec bien moins d'efforts.
La simplification croisée n'est pas une règle mathématique différente. C'est simplement une façon plus efficace d'appliquer les principes de simplification, au moment où les chiffres sont plus faciles à gérer.
Comparaison des approches de simplification
Ce tableau met en évidence les avantages et inconvénients de simplifier avant ou après la multiplication, pour vous aider à choisir la meilleure stratégie selon la situation.
| Caractéristique | Simplification après le calcul | Simplification croisée avant le calcul |
|---|---|---|
| Complexité des nombres | Travaille avec des nombres plus grands, ce qui augmente le risque d'erreurs. | Garde les nombres petits et faciles à manipuler du début à la fin. |
| Rapidité | Souvent plus lent, car la simplification de grands nombres prend plus de temps. | Généralement plus rapide, car les divisions sont plus simples. |
| Clarté du processus | Méthode directe, mais peut devenir confuse avec des chiffres élevés. | Demande de repérer les diviseurs communs, mais rend le calcul final trivial. |
| Idéal pour… | Des multiplications très simples où le résultat est déjà presque irréductible. | Presque toutes les multiplications, surtout celles avec des nombres composés. |
En résumé, bien que les deux méthodes mènent au bon résultat, la simplification croisée est un outil puissant pour rendre vos calculs plus rapides, plus simples et moins sujets aux erreurs.
Comment repérer les occasions de simplifier
Pour maîtriser cette technique, il faut développer un œil pour les diviseurs communs. C'est une compétence qui vient avec la pratique. Une bonne aisance avec les opérations est fondamentale; des difficultés en mathématiques découlent souvent d'une compréhension fragile des structures multiplicatives. Une étude sur les structures multiplicatives a d'ailleurs souligné l'importance de renforcer cette compréhension pour améliorer les compétences globales.
Pour vous aider, gardez ces astuces en tête :
- Les nombres pairs : Si le numérateur et le dénominateur sont pairs, vous pouvez toujours simplifier par 2.
- Finissant par 0 ou 5 : Un nombre se terminant par 0 ou 5 est toujours divisible par 5.
- Somme des chiffres : Si la somme des chiffres d'un nombre est un multiple de 3, alors le nombre lui-même est divisible par 3.
Reconnaître rapidement ces patrons vous fera gagner un temps précieux. Pour un rappel complet de ces trucs, n'hésitez pas à consulter notre guide détaillé sur les critères de divisibilité. La simplification est l'un des outils les plus puissants pour savoir comment multiplier des fractions efficacement.
Gérer les cas particuliers comme un pro
La multiplication de fractions ne se résume pas toujours à un simple calcul entre deux fractions. Dans la pratique, on tombe souvent sur des variantes qui semblent plus complexes, mais qui, en réalité, suivent exactement les mêmes principes. Une fois que vous maîtrisez ces quelques cas de figure, plus aucun problème ne pourra vous prendre au dépourvu.
Ces situations incluent la multiplication d’une fraction par un nombre entier, la gestion des nombres fractionnaires (aussi appelés nombres mixtes), et le calcul en chaîne de plusieurs fractions. Voyons comment aborder chaque scénario avec méthode et confiance.
Comment multiplier une fraction par un nombre entier
C'est un cas de figure très fréquent. Imaginez que vous devez tripler une recette qui demande 3/4 de tasse de farine. Votre calcul est 3 x 3/4. Comment s'y prendre? L'astuce est de voir le nombre entier comme une fraction, tout simplement.
Et c’est incroyablement facile : n'importe quel nombre entier peut s'écrire sous forme de fraction en le plaçant sur un dénominateur de 1. Ainsi, le chiffre 3 devient 3/1.
Votre opération se transforme alors en :
3/1 x 3/4
À partir de là, vous n'avez qu'à appliquer la règle de base :
- Multipliez les numérateurs : 3 x 3 = 9
- Multipliez les dénominateurs : 1 x 4 = 4
- Le résultat est 9/4.
C’est tout! Cette technique fonctionne à tous les coups. Si vous devez calculer 5 x 2/7, vous transformez le 5 en 5/1, et le tour est joué.
Que faire avec les nombres fractionnaires
Les nombres fractionnaires, comme 2 ½, combinent un nombre entier et une fraction. Pour les multiplier, la première étape est absolument essentielle : il faut les convertir en fractions impropres (celles où le numérateur est plus grand que le dénominateur).
Voici comment convertir 2 ½ :
- Multipliez l'entier (2) par le dénominateur (2) : 2 x 2 = 4.
- Ajoutez ce résultat au numérateur de départ (1) : 4 + 1 = 5.
- Conservez le même dénominateur (2).
- Le nombre fractionnaire 2 ½ est maintenant la fraction impropre 5/2.
Une fois que tous vos nombres fractionnaires sont convertis, vous pouvez les multiplier normalement. Par exemple, pour calculer 2 ½ x 1/3, l'opération devient 5/2 x 1/3, ce qui donne 5/6.
Attention à ne pas tomber dans le piège de multiplier les entiers entre eux, puis les fractions. C'est une erreur très commune qui mène à un résultat complètement faux. La conversion en fraction impropre est la seule méthode fiable.
Enchaîner la multiplication de plusieurs fractions
Il arrivera que vous ayez à multiplier trois, quatre, ou même plus de fractions en même temps, comme dans 1/2 x 3/4 x 2/5. La bonne nouvelle? La règle ne change pas d’un pouce. Vous multipliez simplement tous les numérateurs ensemble, puis tous les dénominateurs ensemble.
Pour notre exemple :
- Numérateurs : 1 x 3 x 2 = 6
- Dénominateurs : 2 x 4 x 5 = 40
- Le résultat est 6/40, que l'on peut simplifier pour obtenir 3/20.
Cette approche est directe et efficace. N'oubliez pas que la simplification croisée devient encore plus pratique ici, car elle vous évite de jongler avec de très grands nombres. La maîtrise de ces techniques est fondamentale et constitue une excellente base avant d’apprendre comment diviser des fractions avec la méthode simple.
Mettez vos connaissances à l'épreuve avec nos exercices corrigés

La théorie, c'est bien, mais rien ne vaut la pratique pour vraiment maîtriser un concept. C'est en mettant les mains à la pâte que les nouvelles compétences s'ancrent solidement. Considérez cette section comme votre terrain d'entraînement personnel pour devenir un pro de la multiplication de fractions.
Pour vous accompagner, nous avons concocté une série d'exercices à difficulté progressive. On commencera doucement avec des multiplications simples pour s'échauffer, avant de passer à des problèmes qui exigent une simplification astucieuse, puis on terminera avec des calculs impliquant des nombres entiers ou fractionnaires.
On commence par les bases
Allons-y avec quelques multiplications directes. L'idée ici est de s'assurer que la méthode fondamentale est bien comprise. Visez la précision et la rapidité!
-
Problème 1 : Calculez 2/5 x 3/7
- Solution : On multiplie les numérateurs entre eux (2 x 3 = 6) et les dénominateurs ensemble (5 x 7 = 35). Le résultat est 6/35. La fraction est déjà à sa plus simple expression.
-
Problème 2 : Calculez 1/4 x 5/6
- Solution : En appliquant la même logique, on obtient 5/24 (1 x 5 et 4 x 6). Cette fraction ne peut pas non plus être simplifiée.
Le but n'est pas juste de trouver la bonne réponse, mais de bien comprendre le chemin pour y arriver. Analyser la correction, c'est le meilleur moyen de repérer les petites erreurs qui pourraient devenir de mauvaises habitudes.
Problèmes avec simplification
Maintenant, la simplification entre en jeu. C'est ici que la technique de la simplification croisée va vraiment vous faire gagner du temps et vous éviter des maux de tête.
Chaque exercice corrigé est une chance de confirmer votre raisonnement. Ce n'est pas un test, mais plutôt un dialogue avec vous-même pour vérifier que vous saisissez non seulement le « comment », mais aussi le « pourquoi » de chaque étape.
Problème 3 : Calculez 4/9 x 3/8
- Correction détaillée : Avant même de multiplier, on jette un œil aux chiffres. On voit que 4 et 8 ont un diviseur commun (4), et que 3 et 9 peuvent tous deux être divisés par 3. Notre calcul se transforme donc en 1/3 x 1/2, ce qui donne 1/6. C'est beaucoup plus simple que de devoir simplifier 12/72 après coup!
Comment gérer les nombres entiers et fractionnaires
Ces derniers exercices intègrent les cas un peu plus particuliers que nous avons abordés. La clé ici, c'est d'être rigoureux et de ne sauter aucune étape.
-
Problème 4 : Calculez 5 x 3/10
- Correction détaillée : La première chose à faire est de transformer 5 en fraction, soit 5/1. L'opération devient 5/1 x 3/10. On applique la simplification croisée (5 et 10 sont divisibles par 5), ce qui nous donne 1/1 x 3/2. Le résultat final est 3/2 (ou 1 ½).
-
Problème 5 : Calculez 2 ¼ x 2/3
- Correction détaillée : On doit d'abord convertir le nombre fractionnaire 2 ¼ en fraction impropre. On fait (2 x 4) + 1 = 9, ce qui nous donne 9/4. Le calcul est maintenant 9/4 x 2/3. Grâce à la simplification croisée, on peut réduire 9 et 3 par 3, et 4 et 2 par 2. On se retrouve avec 3/2 x 1/1, pour un résultat final de 3/2.
En pratiquant régulièrement ces différents types de problèmes, vous verrez votre hésitation se transformer en confiance. Chaque multiplication réussie est un pas de plus vers la maîtrise totale. Cette compétence est d'ailleurs fondamentale pour d'autres notions, comme l'addition de fractions, qui suit une logique complètement différente. Pour approfondir le sujet, n'hésitez pas à consulter notre guide sur comment additionner des fractions.
Questions fréquentes sur la multiplication des fractions
Même avec de la pratique, il est tout à fait normal d'avoir encore quelques questions qui trottent dans la tête. C'est le signe qu'on cherche à bien maîtriser le sujet! Pour dissiper les derniers doutes, nous avons regroupé les interrogations les plus courantes.
L'idée ici est simple : vous donner des réponses claires et directes pour que vous puissiez attaquer n'importe quel problème de multiplication de fractions avec une confiance totale.
Faut-il trouver un dénominateur commun?
Non, et c'est une excellente nouvelle! C'est probablement la confusion la plus fréquente. La recherche d'un dénominateur commun est une étape cruciale, mais uniquement pour l'addition et la soustraction de fractions.
Quand on se demande comment multiplier des fractions, on oublie cette étape. On va droit au but : numérateurs ensemble, dénominateurs ensemble. C’est ce qui rend l’opération beaucoup plus simple et rapide.
Comment gérer les signes négatifs?
La règle est exactement la même que pour les nombres entiers, rien de nouveau sous le soleil. On multiplie d'abord les fractions comme si elles étaient positives, puis on s'occupe des signes.
Il suffit de compter le nombre total de signes « moins » dans l'opération :
- Un nombre pair de négatifs (deux, quatre…) : Le résultat final sera positif.
- Un nombre impair de négatifs (un, trois…) : Le résultat final sera négatif.
Par exemple, (-1/2) x (-3/4) donne 3/8. Le résultat est positif, car il y a deux signes négatifs.
Est-ce que multiplier des fractions donne toujours un résultat plus grand?
Pas du tout! C'est une idée reçue tenace, mais c'est le contraire qui se produit souvent. Quand on multiplie deux fractions propres (celles qui sont plus petites que 1), comme 1/2 x 1/2, le résultat est 1/4. Ce 1/4 est en fait plus petit que les fractions de départ.
C'est logique quand on y pense : vous prenez une "partie d'une partie" qui était déjà plus petite qu'un entier. Le résultat ne peut donc être que plus petit lui aussi.
Et si on multiplie par 1 ou par 0?
Ici aussi, les règles de base des mathématiques ne changent pas. Multiplier n'importe quelle fraction par 1 ne la modifie absolument pas. Par exemple, 3/5 x 1 = 3/5. Le 1 est l'élément neutre de la multiplication.
Et pour le 0? C'est encore plus simple. Il absorbe tout. N'importe quelle fraction multipliée par 0 donnera toujours un résultat de 0. Par exemple, 3/5 x 0 = 0.
Si votre enfant a besoin d'un petit coup de pouce pour solidifier ces concepts ou d'autres notions en mathématiques, les tuteurs de Centrétudes offrent un accompagnement personnalisé. Découvrez comment nous pouvons l'aider à bâtir sa confiance et ses compétences sur centretudes.ca.


