Pour calculer la circonférence d'un cercle, aussi appelée son périmètre, on utilise une formule assez simple. En gros, il y a deux avenues possibles : C = 2πr si vous avez le rayon, ou bien C = πd si vous connaissez le diamètre. C’est cette relation mathématique qui est au cœur de tout calcul de la distance autour d’un cercle.
Comprendre la circonférence d'un cercle
Imaginez que vous prenez une roue de vélo et que vous la déroulez jusqu'à ce qu'elle forme une ligne droite. La longueur de cette ligne, c'est exactement la circonférence. Autrement dit, c'est le périmètre du cercle, une mesure de base en géométrie.
Pour trouver cette longueur, une simple règle ne suffit pas. Il faut une formule qui fait le pont entre la distance autour du cercle et une de ses propriétés, comme son rayon ou son diamètre. C’est là que nos fameuses formules entrent en jeu.
Les deux formules essentielles
Tout dépend de l’information que vous avez en main. Heureusement, deux équations équivalentes vous permettent d'arriver au même résultat :
- Si vous connaissez le rayon (r) : Le rayon, c'est la distance entre le centre du cercle et son bord. La formule est alors C = 2 × π × r.
- Si vous connaissez le diamètre (d) : Le diamètre traverse le cercle d'un bord à l'autre en passant par le centre. Dans ce cas, la formule est C = π × d.
Comme le diamètre est simplement le double du rayon (d = 2r), vous comprenez vite pourquoi les deux formules sont interchangeables et donnent toujours le même résultat.
Avant d'aller plus loin, il est bon de résumer les éléments clés de ces formules.
| Symbole | Nom | Définition |
|---|---|---|
| C | Circonférence | La distance totale autour du cercle. |
| π | Pi | Une constante mathématique (~3,14159) qui représente le rapport entre la circonférence et le diamètre d'un cercle. |
| r | Rayon | La distance du centre du cercle à n'importe quel point sur son contour. |
| d | Diamètre | La distance d'un bord à l'autre du cercle, en passant par le centre. C'est égal à 2 fois le rayon (2r). |
Les composants clés de la formule
Ce tableau met en évidence les pièces du casse-tête. Une fois que vous les maîtrisez, calculer la circonférence devient un jeu d'enfant.
Le fameux Pi (π) ! Ce symbole est une constante mathématique absolument incontournable. C'est le rapport fixe entre la circonférence d'un cercle et son diamètre. On l'arrondit souvent à 3,14159, mais en réalité, ses décimales se poursuivent à l'infini sans jamais se répéter.
Un petit voyage dans le temps sur les traces de Pi
La formule de la circonférence d'un cercle, qui nous paraît si simple aujourd'hui, est le résultat d'une quête qui a traversé les millénaires. Bien avant l'invention des calculatrices, les grands penseurs de l'Antiquité s'étaient déjà penchés sur un fait fascinant : peu importe la taille d'un cercle, le rapport entre sa circonférence et son diamètre ne change jamais.

Cette constante mystérieuse, qu'on appelle maintenant Pi (π), est devenue l'un des nombres les plus étudiés de toute l'histoire. Les Babyloniens, autour de 2000 ans avant notre ère, l'avaient déjà estimé à environ 3,125. C'était une approximation franchement impressionnante pour l'époque.
Le coup de génie d'Archimède
C'est au IIIe siècle avant notre ère que le mathématicien grec Archimède a vraiment changé la donne. Il a mis au point une méthode brillante pour calculer la valeur de Pi avec une précision jamais vue auparavant. Son approche était purement géométrique, et surtout, incroyablement astucieuse.
Imaginez un cercle parfait. Archimède a eu l'idée de dessiner un polygone juste à l'intérieur du cercle (inscrit), et un autre juste à l'extérieur (circonscrit). Son raisonnement était simple : la circonférence du cercle est forcément plus grande que le périmètre du polygone intérieur, mais plus petite que celui du polygone extérieur.
En augmentant le nombre de côtés de ses polygones, passant de 6 à 12, puis 24, 48 et même jusqu'à 96, Archimède a réussi à « coincer » la valeur de Pi entre deux nombres de plus en plus proches.
Grâce à cette technique, il a pu établir que Pi se trouvait quelque part entre 3 + 10/71 et 3 + 1/7. La formule que nous utilisons tous, C = 2 × π × r, s'appuie directement sur ses travaux fondamentaux. L'approximation d'Archimède, qui correspond à une fourchette entre 3,1408 et 3,1429, a posé les bases du calcul de la formule de la circonférence d'un cercle pour les 2000 ans qui ont suivi. Pour en savoir plus sur cette méthode, vous pouvez jeter un œil au regard archimédien sur le cercle sur accromath.uqam.ca.
Cette histoire transforme une simple formule mathématique en un véritable témoignage de la persévérance et de l'ingéniosité humaine.
Appliquer la formule pas à pas
Maintenant que la théorie est bien en place, passons à la pratique. Appliquer la formule de la circonférence d’un cercle est en fait assez simple : il suffit de mesurer, puis de multiplier. Que vous calculiez le tour d’une roue de vélo ou d’une pizza, la logique reste exactement la même.
Cette infographie résume bien le processus en trois étapes claires, de la prise de mesure jusqu'au résultat final.
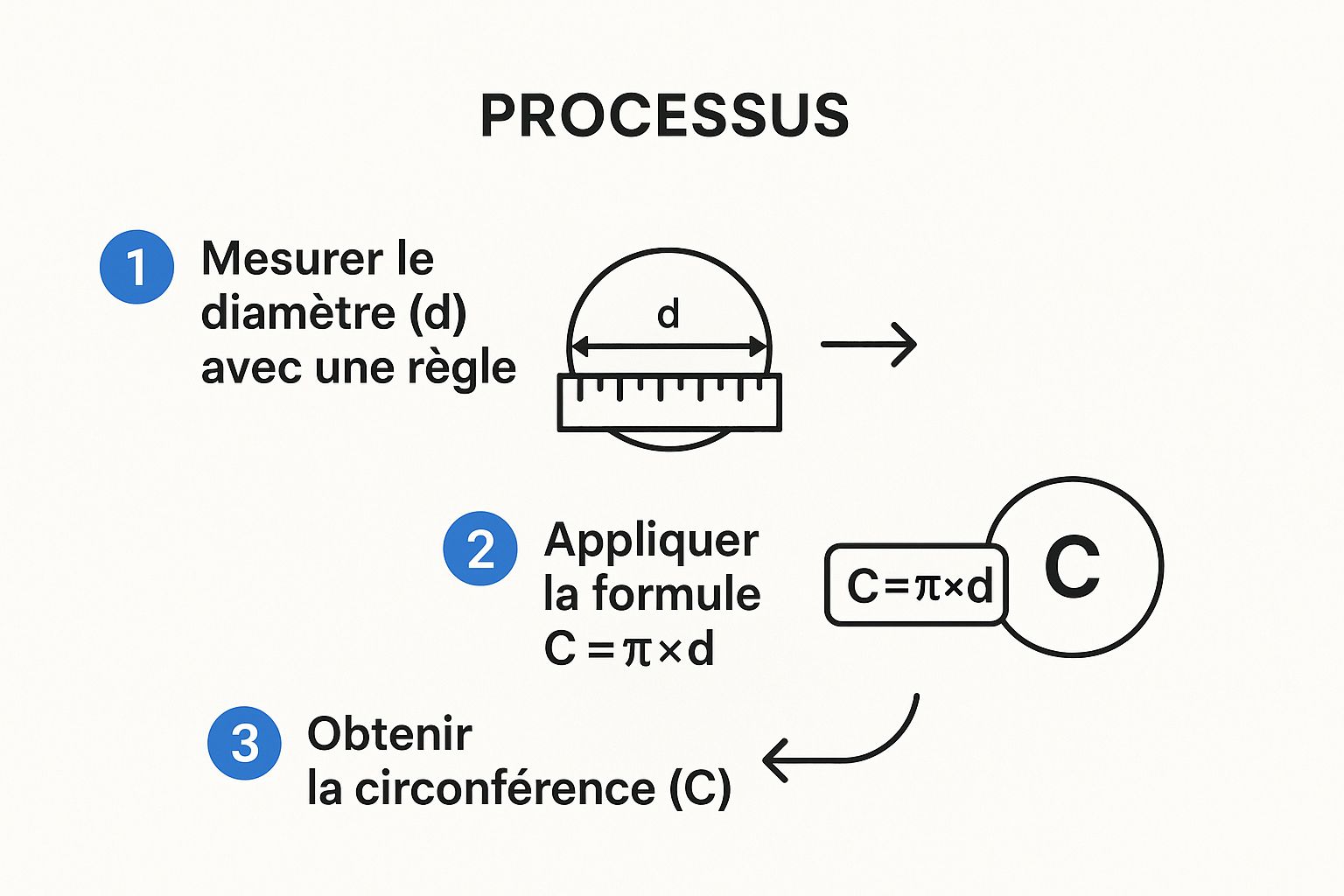
Comme vous le voyez, la démarche est directe. On transforme un concept géométrique en un calcul accessible à tous.
Exemple 1 : Calculer avec le diamètre
Imaginons que vous commandez une grande pizza avec un diamètre de 35 centimètres (cm). Pour savoir quelle longueur de croûte vous allez pouvoir savourer, il faut trouver la circonférence.
- Identifier la formule : Puisqu'on connaît le diamètre (d), la formule la plus simple est C = π × d.
- Remplacer les valeurs : On insère le diamètre dans la formule, ce qui nous donne C = π × 35 cm.
- Calculer le résultat : En utilisant une approximation de Pi (3,14159), le calcul devient C ≈ 3,14159 × 35.
Résultat : La circonférence de la pizza est d'environ 109,96 cm. C'est presque 1,10 mètre de délicieuse croûte à partager!
Exemple 2 : Calculer avec le rayon
Prenons cette fois-ci une roue de vélo pour enfant. Vous mesurez la distance entre le centre de la roue et le pneu (le rayon) et vous obtenez 20 cm.
- Choisir la bonne formule : Avec le rayon (r), on prend plutôt C = 2 × π × r.
- Insérer les données : L'équation devient alors C = 2 × π × 20 cm.
- Effectuer le calcul : On multiplie tous les chiffres. C ≈ 2 × 3,14159 × 20.
Le résultat final nous donne une circonférence d'environ 125,66 cm.
Que vous utilisiez la touche π de votre calculatrice pour plus de précision ou l'approximation 3,14, le processus ne change pas. Pour devenir encore plus rapide, jetez un œil à nos conseils pour exceller en calcul mental et effectuez ces opérations en un clin d'œil.
Observer la formule en action dans le monde réel
Loin d'être un simple exercice scolaire, la formule de la circonférence d'un cercle est un outil essentiel qui a littéralement façonné notre monde. On la retrouve cachée dans des objets du quotidien et dans de grandes prouesses techniques, prouvant que la géométrie est bien plus qu'une matière abstraite.

Pensez aux ingénieurs qui conçoivent un tunnel. Ils doivent calculer avec une précision extrême la quantité de matériaux nécessaires pour le revêtement intérieur, une tâche impossible sans maîtriser la circonférence. De même, la conception de pièces mécaniques comme les engrenages ou les roulements à billes dépend entièrement de ce calcul pour assurer un mouvement fluide et sans friction.
De l'urbanisme à l'exploration spatiale
Les applications de cette formule sont vastes et souvent surprenantes. Voici quelques exemples concrets qui montrent son utilité partout autour de nous :
- Urbanisme : Les urbanistes utilisent la circonférence pour planifier des ronds-points efficaces. Ils calculent la longueur des voies de circulation pour optimiser le flux des véhicules et assurer la sécurité.
- Aérospatiale : Les scientifiques calculent l'orbite des satellites en se basant sur des principes circulaires. La circonférence de l'orbite est un facteur clé pour déterminer la vitesse et la période de révolution du satellite autour de la Terre.
- Fabrication : Dans l'industrie, le calcul de la circonférence est crucial pour déterminer la longueur de matériau nécessaire pour fabriquer des objets cylindriques comme des tuyaux, des boîtes de conserve ou des câbles.
Cet outil va bien au-delà des objets manufacturés. Il nous permet de comprendre notre monde à une échelle planétaire.
L'un des exemples les plus marquants de son pouvoir est l'exploit d'Ératosthène. En 240 avant J.-C., ce savant grec a utilisé des principes géométriques liés au cercle pour calculer la circonférence de la Terre. Sa mesure, d'environ 39 375 km, n'était qu'à 1,7 % de la valeur réelle, une prouesse incroyable pour l'époque.
Ces exemples montrent que maîtriser la circonférence, c'est aussi comprendre le fonctionnement de structures plus complexes. Pour aller plus loin, vous pourriez par exemple découvrir comment calculer l'aire d’un cylindre, un calcul qui combine directement la circonférence et la hauteur d'un objet.
Éviter les erreurs de calcul courantes
Même avec la bonne formule de circonférence de cercle en main, une simple distraction peut vite nous mener à un résultat erroné. Heureusement, la plupart des erreurs sont assez classiques et faciles à éviter une fois qu’on les connaît.
L’erreur la plus fréquente? Confondre le rayon et le diamètre. C’est le piège numéro un. Imaginez un cercle de 10 cm de diamètre. Si, par inattention, vous traitez ce 10 cm comme un rayon dans la formule C = 2πr, votre calcul donnera C = 2 × π × 10 = 20π, soit environ 62,8 cm. Or, le bon résultat, avec la formule C = πd, est tout simplement 10π, soit 31,4 cm. Votre réponse serait alors deux fois trop grande!
Une autre petite erreur qui se glisse souvent dans les calculs concerne la valeur de Pi (π). Utiliser 3,14 est parfait pour des estimations rapides, mais ça peut manquer de précision pour des travaux plus techniques. Pour un cercle de 2 mètres de rayon, l'approximation donne 12,56 mètres. En utilisant la touche π de la calculatrice, on obtient environ 12,56637 mètres. Cette petite différence peut sembler minime, mais en ingénierie, elle peut avoir de grandes conséquences.
Une liste de vérification rapide
Pour être certain que vos calculs sont justes, prenez l’habitude de vérifier ces trois points avant de donner votre réponse finale :
- Avez-vous la bonne mesure? Assurez-vous d’utiliser le rayon (r) avec C = 2πr et le diamètre (d) avec C = πd. Ne les mélangez surtout pas.
- Les unités sont-elles cohérentes? Si votre rayon est en centimètres, votre circonférence le sera aussi. Les erreurs d’unité sont courantes, surtout quand des conversions sont nécessaires. Pour en savoir plus, jetez un œil à notre guide sur la conversion de mesures.
- Quelle précision pour Pi? Avez-vous besoin d’une simple estimation (3,14) ou d’un calcul plus précis (la touche π de votre calculatrice)? Le choix dépend vraiment du contexte de votre problème.
Le conseil du pro : Prenez une seconde pour visualiser le cercle dans votre tête. Un rayon, c'est toujours la moitié du diamètre. Cette simple image mentale est un excellent réflexe pour ne pas tomber dans le piège le plus commun et pour avoir confiance en vos résultats.
L'importance de la formule aujourd'hui
Loin d'être une simple relique des manuels de mathématiques, cette formule antique est plus pertinente que jamais à notre époque. La formule de la circonférence d'un cercle est en fait au cœur de nombreuses technologies qui façonnent notre quotidien.
Des systèmes GPS qui calculent les distances sur notre planète sphérique aux logiciels de conception assistée par ordinateur (CAO) qui modélisent des pièces avec une précision chirurgicale, ce calcul fondamental est partout. C'est le pilier silencieux de multiples innovations.
Un outil indispensable pour l'industrie
Dans le monde de l'ingénierie, cette formule n'est pas une abstraction, mais un outil de travail de tous les jours. Les concepteurs s'en servent pour créer des pièces mécaniques circulaires comme des engrenages ou des roulements, où chaque millimètre compte pour garantir un fonctionnement sécuritaire et optimal.
Les chiffres parlent d'eux-mêmes : près de 65 % des calculs en CAO pour des pièces mécaniques circulaires reposent directement sur ce principe. De même, environ 48 % des projets de génie civil qui impliquent des structures cylindriques utilisent cette formule, un fait illustré par des applications historiques comme le calcul de la circonférence de la Terre par Ératosthène, exploré dans l'article sur la géométrie dans les sciences sur echosciences.nouvelle-aquitaine.science.
Cette connaissance fondamentale soutient des industries de pointe comme l'aérospatiale, la robotique et même l'animation 3D, où la perfection du mouvement circulaire est non négociable.
Voilà la preuve qu'un concept ancien peut demeurer un outil bien vivant et indispensable au progrès. Cette même logique géométrique sert d'ailleurs de base à des calculs plus complexes, comme ceux que nous abordons pour déterminer le volume du cône dans notre guide complet.
Finalement, comprendre la circonférence aujourd'hui, c'est détenir une clé pour décoder le fonctionnement de notre monde, de la plus petite pièce d'un moteur à la trajectoire d'un satellite en orbite.
Questions fréquentes sur la circonférence
Même après avoir bien compris la formule de la circonférence d’un cercle, il reste souvent quelques questions pratiques. C’est tout à fait normal. Prenons un moment pour clarifier les derniers détails qui vous permettront de faire vos calculs en toute confiance.
Une des premières questions qui vient en tête est : quelle formule choisir? C = 2πr ou C = πd?
En fait, la réponse est très simple. Les deux formules sont parfaitement identiques et vous donneront toujours le même résultat. Le choix dépend simplement de l’information que vous avez sous la main. Si vous connaissez le rayon, allez-y directement avec C = 2πr. Si c’est le diamètre que vous avez, la formule C = πd vous évitera un calcul intermédiaire.
Un autre point important : la précision de Pi (π). Pour la majorité des devoirs ou pour une estimation rapide, l’approximation de 3,14 fait amplement l’affaire. Par contre, si vous travaillez sur un projet qui demande plus de rigueur, comme en ingénierie, il vaut mieux utiliser 3,1416 ou, encore plus simple, la touche π de votre calculatrice scientifique.
Inverser la formule pour trouver le rayon
Maintenant, que faire si le problème est à l’envers? Par exemple, si vous connaissez la circonférence, mais que vous devez trouver le rayon ou le diamètre?
Il suffit de manipuler un peu la formule de départ. Pour trouver le rayon (r) à partir de la circonférence (C), on part de C = 2πr et on cherche à isoler « r ».
Pour y arriver, on divise simplement chaque côté de l’équation par 2π. On obtient alors une nouvelle formule bien pratique :
- r = C / (2π)
Et pour trouver le diamètre (d), c’est encore plus direct :
- d = C / π
Ces formules inversées sont vraiment utiles dans toutes sortes de situations concrètes. Si ce genre de manipulation algébrique vous donne du fil à retordre, un service de tutorat en mathématiques pour le secondaire peut être d’une grande aide pour solidifier ces bases et rendre les maths beaucoup plus abordables.
Chez Centretudes, nous transformons les défis mathématiques en réussites. Si votre enfant a besoin d'un coup de pouce pour maîtriser des concepts comme la circonférence, nos tuteurs certifiés sont là pour l'accompagner. Découvrez nos programmes personnalisés sur https://centretudes.ca.


